基于最短路方法的生物序列比对问题研究

Posted 2020-10-07

1. 概述

作为生物信息学中的基本组成和重要基础，生物序列比对旨在找出两个或多个生物序列之间的相似性，发现生物序列中的功能、结构和进化信息。

生物序列比对在现实生活中有广泛的应用价值。从核酸和蛋白质序列出发,分析序列中表达结构和功能的生物信息；在序列分析中,将未知序列同已知序列进行相似性比较是一种强有力的研究手段,从序列的片段测定,拼接,基因的表达分析,到RNA和蛋白质的结构功能预测,物种亲缘树的构建都需要进行生物分子序列的相似性比较。本软件主要是对双序列的DNA序列进行比较，以确定两条序列的相似性。

本软件对张军英老师的最小资源神经网络（MRNN）算法进行了一定的改进，使其可以运用到双序列基因比对上面来。

本软件主要实现的功能有：

能够对两条DNA序列进行比对，得到两条序列的最佳匹配路径，并计算两条序列的相似度。

本软件的主要特点包括：

（1）本软件采用了神经网络结构，比较适合求解较大规模的生物序列比对问题。

（2）将最小资源神经网络（MRNN）算法运用到生物序列比对当中，并将此算法与动态规划算法进行比较，分别得到使用这两种算法进行DNA序列比对所花费的CPU时间。

（3）本软件专门适用于双序列比对，不适用于多序列比对。

2．软件实现设计

2.1 软件技术方案

本软件的主要功能只有一个，即为对两条DNA序列进行比对，给出最佳的匹配路径以及匹配度，并分别给出使用动态规划算法和最小资源神经网络（MRNN）算法的CPU时间。

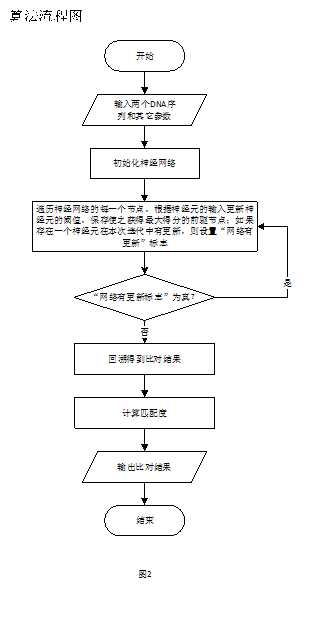
图2给出了求解DNA双序列比对软件设计的技术方案，按照如下步骤找出从源神经元到终点的最佳匹配路径。

 

 

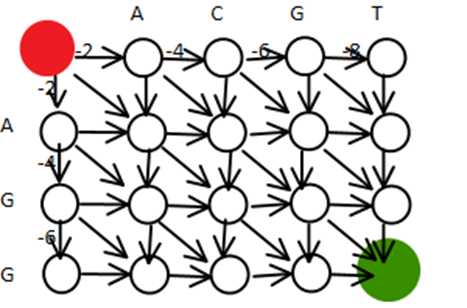
图1 DNA序列和与之有关的图结构

 

2.1.1 求解DNA双序列比对技术方案包括以下步骤：

1. 初始化两条DNA序列图以及图的数据结构

   如图1所示：要比较的两个DNA：DNA1为ACTG，DNA2为AGC。

   为两个序列生成的图如上图所示，以上每个圆圈为一个神经元，保存前驱信息（包括左边，上边和左上边三个，若是可经由某个前驱可达，则保存该前驱的位置信息，可达指的是从源点到该神经元的路径小于阈值最小值）和从原点到该点的路径最大长度（我们把它称作阈值，后面提到阈值均代表这个意思，注意神经元的输出等于它的阈值），及神经元的坐标x,y。 为每个点规定横纵坐标，则，源点（即源神经元，后面简称源点）为红色神经元（0,0），终点（即终点神经元，后面简称终点）为绿色神经元(3,4),

   其他点依次类推。规定的罚分规则如下（分值即与MRNN算法中的路径长度相对应，这里MRNN中路径最小值即是这里的分值最大值）：

   从源点往前走，下一个神经元相对于本神经元，横坐标不变纵坐标加一，罚分-2，纵坐标不变横坐标加一时，罚分-2，横纵坐标均加一时，看碱基是否相同，相同时+3，不同时-1。直到终点。

   算法一开始，初始化图中每个神经元的阈值最小值为-100，前驱神经元为0个，前驱神经元状态为0，源点的阈值为0。

2. 遍历图中所有的神经元

   我们采用的遍历方式（更新每一个神经元的状态为一次遍历过程）是从终点到源点的遍历，对每一个神经元的更新，包括更新它的阈值，可达路径的前驱神经元信息。后面会详细说明更新的过程。

   这里说明下为什么采用从终点到源点的遍历方式：

   MRNN算法中，严格的按照t+1则增加一跳并更新增加了这一跳所改变的神经元的状态（包括阈值等）；而对于生物序列对比的图见上，每一次遍历过程，是增加一跳的过程（按照MRNN算法来进行），直到收敛，所以若是从源点到终点，则原本需要两跳才能得到阈值最大值的神经元，经过一次遍历，就能得到该神经元的最大值。（例如：（1,1）位置的神经元，从源点到终点的遍历方式中，遍历到该神经元时，它的三个前驱神经元均已经收敛（得到阈值最大值，上和左前驱是在这次遍历同时更新的）），所以在更新它的状态（阈值等）时能得到阈值最大）。

   而从终点到源点遍历时，由于神经元的左和上前驱是后于该神经元更新的，所以该神经元不会受到影响。

3. 更新神经元的过程：

   在遍历的过程中要更新神经元的信息：对于每一个神经元，先判断它的上前驱神经元到它是否可达，若可达则比较该路径的分值（加上罚分后）是否大于该神经元的阈值，大于则更新阈值并更新前驱数量为1和前驱位置，等于则说明存在相同的分值的路径，保存多个前驱信息（最多三个前驱均保存），其他情况忽略，左边前驱神经元处理过程同上前驱。

   对于这个神经元的左上前驱神经元，先判断这个神经元的位置对应的碱基是否相同，若相同则罚分为+3，不同为-1，再在这两种情况下分别进行更新阈值和前驱信息（同上前驱）。

   为避免重复保存多条一模一样的路径，保存了前驱神经元具体是左上，上，还是左的信息，这里简单说明。

4）判断图是否收敛

判断图是否收敛，若在一次遍历的过程结束后没有神经元的状态信息发生改变且到达终点，则已经收敛。若收敛，则输出结果，若不收敛，则再遍历图中的所有神经元。

2.1.2 算法迭代示意图如下所示：

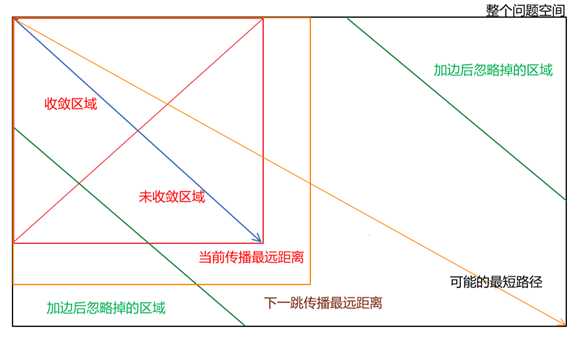
图2 算法迭代图示

（说明：收敛区域内的所有神经元已经收敛，未收敛区域的神经元还需要遍历，加边后忽略的区域见上，每一跳传播的最远距离均是对角线距离，除了到达终点后的条，可能的最短路径长度为最大的碱基长度）

2．2软件设计流程

根据2.1节所述的软件设计方案，本软件设计流程如下：

本软件设计共分为以下三个部分:使用动态规划算法对两条DNA序列进行比对，计算出所花费的CPU时间；使用最小资源神经网络算法对两条DNA序列进行比对，给出最佳匹配路径，并计算所花费的CPU时间。

（1）使用最小资源神经算法对两条DNA序列进行比对

程序名：mrnn.cpp

输入要对比的序列所在的两个文件文件名，从而获取两条DNA信息

输入图的第几个神经元进行加边，（从零开始）

（1a）输入文件为从网上下载的两条DNA序列的碱基对

（1b）存储两条DNA序列所构成图的类Graph的数据结构：

本软件用来比对两条DNA序列的相似度，所以采用链接链表存储结构。

图的数据结构定义在头文件graph.h中；

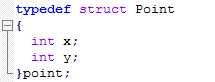
图3 图神经元数据结构代码

图中每个神经元的由神经元的横坐标和纵坐标组成，数据结构如图3所示：

图4 图的数据结构代码

图中的每个神经元由保存源点到该点的路径长length,最多三个直接前驱神经元pre_neuron[3],前驱神经元的数量，前驱神经元的情况sig_haspre四项组成，数据结构如图4所示：

输出为寻找两条DNA序列的最佳匹配路径，以及最小资源神经网络算法进行序列比对所花费的CPU时间。

图5为寻找两条DNA序列的最佳路径的关键代码：

 

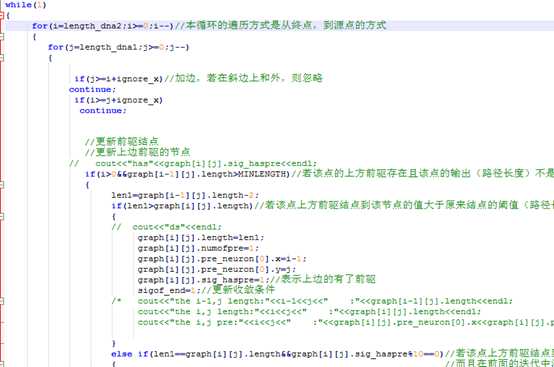
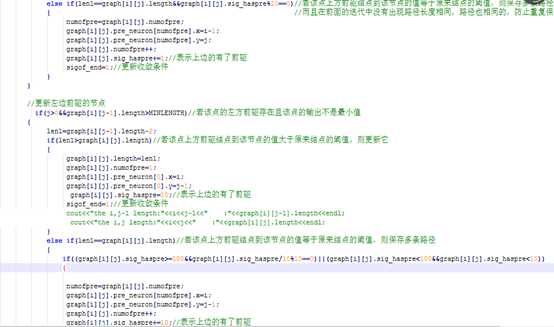
图5 寻找两条DNA序列的最佳路径的关键代码

（2）使用动态规划算法对两条DNA序列进行比对

程序名：nw.cpp

输入要对比的序列所在的两个文件文件名，从而获取两条DNA信息

。程序运行的结果输出到文件result.txt中。

3、动态规划算法和最小资源神经网络（MRNN）算法的比较分析

3.1算法性能测试

软件的使用方式如下图所示：

 

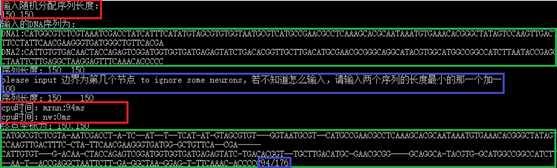
1. 输入参数：两个随机序列的长度。因为两个序列都由程序随机生成，所以它们的匹配度无法保证，但通常比较低。（后来我们又测试了真实的DNA序列片段，结果显示匹配度比较高，结果如后文表格。）
2. 输出：随机生成的DNA序列。
3. 输入参数：边界位置。此边界即加边优化需要的边界位置。这意味着边界之外的节点将不会出现在比对结果里面。
4. 输出：MRNN算法运行的时间和动态规划算法运行的时间（ms）。
5. 输出：一对比对结果序列，且具有最大的匹配度。为了显示方便，图中只显示了一对结果。事实上，对应于一种最大得分，可能存在很多种比对结果。
6. 输出：匹配度。匹配度使用未约简的分数表示，分母表示比对后的序列长度，分子表示匹配的对数。

 

 

根据以上的程序，我们分别测试了在高匹配度（真实同源DNA序列）和低匹配度（随机生成）情况下的序列，结果如下：

 

高匹配度：

 

序列长度(bp)	CPU时间（ms）			加边情况	匹配度
	NW	MRNN改进	MRNN
150	15	16	16	1	147/150
200	15	0	16	1	1
250	16	15	47	1	0.996
300	16	31	110	3	229/301
350	31	31	156	2	336/351
400	47	47	204	2	1
450	78	47	281	2	448/450
500	62	110	406	4	496/500

 

表格说明和结果分析

1. 此测试运行在序列高匹配度的情况下（对应于同源DNA序列）。由"加边情况"一栏可以看出：即使很小的加边参数也能获得和动态规划算法一样的最优匹配结果。
2. NW（动态规划）算法和MRNN算法的运行时间随着序列长度的增加而增加，而MRNN改进算法的运行时间不符合此规律。这跟MRNN改进算法的加边情况有关。
3. NW算法的运行时间在以上任何规模下都短于MRNN算法。说明在算法改进前，MRNN算法相比于NW算法没有时间上的优势。
4. MRNN改进算法有效地减少了MRNN算法运行的时间。对比NW算法，两者在不同的问题规模下互有优势。
5. 三种算法得出的匹配度相同，说明三种算法相互验证之下的正确性。

 

低匹配度：

 

序列长度(bp)	CPU时间（ms）			加边情况	匹配度
	NW	MRNN改进	MRNN
150	0	47	94	100	94/176
200	16	78	156	70	116/222
250	15	156	344	100	156/291
300	16	250	547	120	186/337
350	46	453	954	150	216/408
400	47	688	1360	180	241/451
450	62	922	1969	200	279/517
500	94	1704	2672	240	312/573

 

表格说明和结果分析

1. 此测试运行在序列低匹配度的情况下（对应于随机生成的DNA序列）。由"加边情况"一栏可以看出：只有在很大的加边参数情况下才能获得和动态规划算法一样的最优匹配结果。
2. 三种算法的运行时间都随着序列长度的增加而增加。
3. 运行时间：NW < MRNN改进 < MRNN。MRNN改进算法相比于MRNN算法在运行时间上有一定程度的改善，但相比于动态规划算法劣势明显。
4. 三种算法得出的匹配度相同，说明三种算法相互验证之下的正确性。

3.2实验结果分析

在考虑空间充足的情况下，这里主要比较时间复杂度:跟问题的规模是什么关系（主要是访问内存和比较用到），图的稀疏度均为3，节点数量是边的三分之一

对于NW动态规划方式来讲：具体实现不讲，主要分析时间复杂度：

假设序列为n,m,则问题规模：图的大小为(n+1)*(m+1),则对于动态规划算法，总体上遍历一遍图，之后便可以回溯输出，遍历整个图的时候访问了多少个点，比较次数是多少？

访问：边界点只有一个前驱，为n+m个点（(0,0)点本身不用）只有一个前驱，访问为(n+m)，比较次数为0,为：m+n

其他点（mn个）：每个点三个前驱，求得最大值要比较两次(不考虑相同路径），故每个点除了访问他自身，还有三个前驱，和两次比较，为6*mn

总共：6mn+m+n=O(mn);

对于MRNN方式来讲：具体实现不讲，主要分析时间复杂度：

假设序列为n,m,则问题规模：图的大小为(n+1)*(m+1),则对于MRNN算法，总体上遍历多遍图（直到收敛），之后便可以回溯输出，遍历整个图的时候访问了多少个点，比较次数是多少？

访问：由于每次遍历所有的点，故为(m+1)*(n+1),收敛时停止，最快收敛时遍历次数：num=max(m,n),每访问一个点，同样访问前驱三个点，除了边界，故为（3mn+m+n）*num;

比较次数：由于每次都要比较，总的比较次数最少为2mn

所以最少时间为：num*(3mn+m+n)+2mn=O(num*mn)

所以从理论上讲，NW优于MRNN

考虑MRNN加边时，若加边t,则去了t*t个神经元，减少了访问和2*t*t的比较，考虑最多去掉min=min(n,m),则

复杂度：num*(3mn+m+n)+2mn-3*min*min

假设n>m:则为：n*(3mn+m+n)-2mn-3mm=3mnn-3mm=3m(nn-m)=O(mnn)

若改进实现：每次迭代不是遍历所有的点：

则按照算法：需要访问的次数为：

（1+2）+（1+2+3）+（1+2+3+4）+…迭代至少n次收敛.=n(n+1)(n+2)/6=O（n^3）（假设nm一样长）加边之后数量级亦不变。

若不一样长，类似。

故最后的结果还是不如动态规划

重点在于NW遍历一次而MRNN遍历多次到收敛，而收敛的最小遍历次数为跳数的最小值，即max(m,n)，导致了MRNN复杂度高，速度不够

4、功能详细设计

4．1软硬件环境

本软件在Dev C++环境下编码实现，功能较完善，开发及应用环境要求较低，普通电脑均可运行。

配置的相关基本要求（最低配置要求）如下;

软件环境要求：

操作系统为Windows7/10，推荐使用Windows 10；

硬件环境要求：

处理器：要求486处理器以上，推荐使用Pentium或更高档处理器的PC兼容机，建议主频在1.6GHZ以上；

内存：512MB以上的内存，推荐使用1G以上的内存；

硬盘：推荐使用80G的硬盘空间。

4.2 功能介绍

利用本软件只能对两条DNA序列进行比对，分别使用动态规划算法和最小资源神经网络算法对DNA序列进行比对，给出最佳匹配路径，并分别计算用着两种方法进行比对所花费的CPU时间。

4.3 注意事项

（1）数据预处理

输入所需的两条DNA序列的格式为.txt格式，文件中包含两条DNA序列的碱基对，除此之外，还得手动输入序列长度以及从图的第几个神经元开始进行夹边。

（2）运行时间

本软件运行时间取决于两条DNA序列的长度。本软件只适用于对两条DNA序列进行比对。因此，使用者需要注意软件的适用情况，保证软件的正常运行。

附录1

关于在动态规划算法中使用匹配度取代打分系统作为优化函数的实验和结果分析

基于匹配度的算法的实现与基于打分系统的动态规划算法类似，不再详述。

结果表明，使用基于匹配度的动态规划算法，可以获得比基于打分系统的动态规划算法获得更优的匹配度。即基于打分系统的动态规划算法并不是总能获得最大的匹配度。

有如下例子：

1，使用打分系统获得的比对结果：

 

 

 

 

 

 

 

    2，使用匹配度获得的比对结果：

 

 

 

 

 

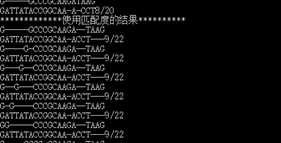
可以看出，对于同一对DNA序列使用两种方式得到的比对结果：

评价方式 获得方式	得分	匹配度
打分方式	5（最大）	8/20
匹配度方式	3	9/22（最大）

由上，得到结论：得分最优并不意味着匹配度最优。

进一步研究

通过查阅资料，我们认为：最优的匹配度（相似度）并不是序列比对的目标。但是在不同的结果序列具有相同的最大得分的情况下，匹配度可以作为辅助评价的参数，可以对比对结果进行进一步的比较。序列比对的最终目标是对两条序列的同源性做出尽可能准确的评价（通常高的匹配度或者相似性并不代表高的同源性）。

通常实用的打分系统都很复杂，会使用"打分矩阵"表示。

 

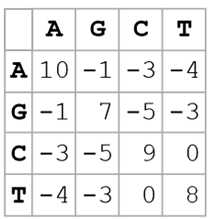
矩阵对角线上的元素表示在匹配的情况下的得分情况；非对角线上的元素表示在失配的情况下的罚分情况。不同的匹配结果可能获得不同的得分，不同的失配结果可能意味着不同的罚分，这些都是基于具体的生物学意义而获得的经验结果或者统计结果。几条有意义的经验如下：

1. 在失配的情况下，转换比颠换更容易发生（统计结果）

   

 

 

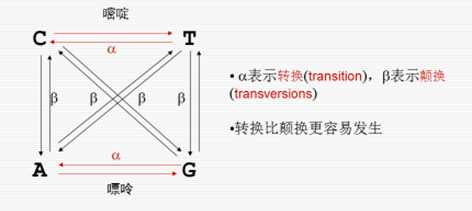
1. 最优的序列比对结果通常需要尽可能少地加入空位
2. 连续空位好于多个非连续的单个空位（相应于基因的连续缺失）

由以上的信息可以得知：序列比对的目标是尽可能揭示两条序列的同源性信息。但是通常匹配度（相似性）高的结果，并不一定是基于生物进化的真实情况的逆反过程的结果。为了揭示生物的同源性，有必要基于一些启发式的知识获得比较好的打分系统。但是同源性又是一种定性的概念，没有准确的评价系统，需要专业的生物学知识辅助判断，因此当前的评分系统都是不完全可靠的。动态规划的算法可以在打分系统固定的情况下获得最优的比对结果，但是结果的进一步评价需要那些具体的生物学背景信息——包括而不限于匹配度（相似性）。

参考文献：

Zhang J, Zhao X, He X. A Minimum Resource Neural Network Framework for Solving Multiconstraint Shortest Path Problems[J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(8):1566.