数据结构－二叉树笔记

Posted 2020-10-07 pathjh

看完《数据结构与算法分析》（c描述）后对二叉树的一点总结

树的节点声明：

 1 typedef  int ElementType;
 2 typedef struct  TreeNode* Position;
 3 typedef Position  BiSearchTree;
 4 
 5 struct TreeNode
 6 {
 7 ElementType Element;
 8 Position Left,Right;
 9 
10 };

二叉查找树的定义如下：

1.二叉查找树首先是一棵二叉树；

2.二叉查找树除了是二叉树外，还具有以下性质：对于树中的任何一个节点X，其左子树中的所有节点的关键字均小于X的关键字的值；而其右子树中的所有关键字的值均大于X的关键字的值。

二叉查找树的常用操作：

BiSearchTree MakeEmpty(BiSearchTree Tree);
Position FindMin(BiSearchTree T);
Position FindMax(BiSearchTree T);
BiSearchTree Insert(ElementType X,BiSearchTree T);
BiSearchTree Delete(ElementType X, BiSearchTree T);

树的操作过程中大多数用到了递归，理解起来相对简单，下面主要讲一下删除操作

对于要被删除的节点

1. 如果节点是一片树叶，那么可以直接删除
2. 如果节点有一个儿子，则该节点可以在其父亲节点调整指针绕过该节点后被删除，如图

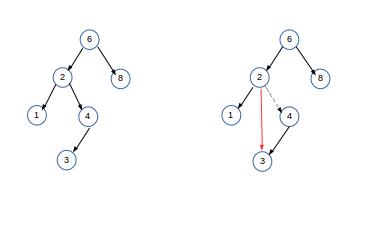
　　　若要删除节点４，则只需将其父亲节点２调整指针指向４的儿子节点３，如右图。需要注意的是，所删除的节点只有在指向它的指针已被省去的情况下才能被去掉

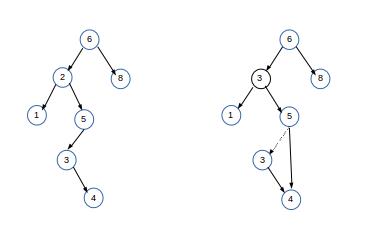
　　３．对于有两个儿子的节点。一般用其右子树中的最小的数据代替该节点的数据，并用递归的方法同样去删除掉那个节点。因为右子树中的最小的节点不可能有左儿子，所以第二次删除就很容易。如下图显示一颗初始的树及其一个节点被删除后的结果。要被删除的节点是根的左儿子，其关键字为２．它被右子树中的最小数据３所代替，然后关键字３的原节点如前例那样被删除

二叉树的常用操作：

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 
  4 
  5 typedef  int ElementType;
  6 typedef struct  TreeNode* Position;
  7 typedef Position  BiSearchTree;
  8 
  9 struct TreeNode
 10 {
 11 ElementType Element;
 12 Position Left,Right;
 13 
 14 };
 15 
 16 BiSearchTree MakeEmpty(BiSearchTree Tree);
 17 Position FindMin(BiSearchTree T);
 18 Position FindMax(BiSearchTree T);
 19 BiSearchTree Insert(ElementType X,BiSearchTree T);
 20 BiSearchTree Delete(ElementType X, BiSearchTree T);
 21 
 22 
 23 //建立一颗空树
 24 BiSearchTree MakeEmpty(BiSearchTree Tree)
 25 {
 26     if(!Tree)
 27     {
 28         MakeEmpty(Tree->Left);
 29         MakeEmpty(Tree->Right);
 30         free(Tree);
 31     }
 32 
 33     return NULL;
 34 }
 35 
 36 //二叉查找树的查找
 37 Position Find(ElementType X,BiSearchTree T)
 38 
 39 {
 40     if(T==NULL)
 41     {
 42         return NULL;
 43     }
 44     else
 45     {
 46         if(X<T->Element)
 47         {
 48             return Find(X,T->Left);
 49         }
 50         else if(X>T->Element)
 51         {
 52             return Find(X,T->Right);
 53         }
 54 
 55         else
 56         {
 57             return T;
 58         }
 59     }
 60 
 61 }
 62 
 63 
 64 //查找最小值（递归写法）
 65 Position FindMin(BiSearchTree T)
 66 {
 67     if(T==NULL)
 68     {
 69         return NULL;
 70     }
 71     else
 72     {
 73         if (T->Left==NULL)
 74         {
 75             return T;
 76         }
 77         else
 78         {
 79             return FindMin(T->Left);
 80         }
 81     }
 82 }
 83 
 84 
 85 //查找最大值（非递归写法）
 86 Position FindMax(BiSearchTree T)
 87 {
 88    if(T!=NULL)
 89    {
 90         while(T->Right!=NULL)
 91         {
 92             T=T->Right;
 93         }
 94    }
 95     return T;
 96 }
 97 
 98 
 99 
100 //插入元素
101 BiSearchTree Insert(ElementType X,BiSearchTree T)
102 
103 {   if(T==NULL)             //树为空时
104     {
105         T=malloc(sizeof(struct TreeNode));
106         if(T==NULL)
107         {
108             fprintf(stderr,"out of place");//stderr:标准错误文件
109         }
110         else
111         {
112             T->Element = X;
113             T->Left=NULL;
114             T->Right=NULL;
115         }
116     }
117     else                //树不为空时
118     {
119         if(X<T->Element)
120         {
121             T->Left=Insert(X,T->Left);
122         }
123 
124         if(X>T->Element)
125         {
126             T->Right=Insert(X,T->Right);
127         }
128         else
129         {
130              //do nothing
131         }
132     }
133 
134     return T;
135 }
136 
137 
138 
139 
140 //删除节点X
141 BiSearchTree Delete(ElementType X,BiSearchTree T)
142 {
143     Position TmpCell;
144     if(T==NULL)
145     {
146         fprintf(stderr,"Element does not exist!");
147     }
148     else if(X<T->Element)
149     {
150         T->Left=Delete(X,T->Left);
151     }
152     else if(X>T->Element)
153     {
154         T->Right=Delete(X,T->Right);
155     }
156     else if(T->Left&&T->Right)         //被删节点有两个孩子
157     {
158         TmpCell = FindMin(T->Right);
159         T->Element = TmpCell->Element;
160         T->Right = Delete(T->Element,T->Right);
161     }
162     else                         //被删节点有１个或是没有孩子
163     {
164         TmpCell =T;
165         if(T->Left==NULL)
166         {
167             T=T->Right;
168         }
169           if(T->Right==NULL)
170         {
171             T=T->Left;
172         }
173         free(TmpCell);
174     }
175     return T;
176 }
177 
178 
179 int main()
180 {
181     BiSearchTree T;
182     int index;
183     int arr[11]={2,8,45,78,111,354,5,676,89,34,45};
184     T=NULL;
185     for(index=0;index<11;index++)
186     {
187         T=Insert(arr[index],T);
188     }
189     T=Insert(100,T);
190     T=Insert(11,T);
191     printf("最小数是：%d\\n",FindMin(T)->Element);
192     printf("最大数是：%d\\n",FindMax(T)->Element);
193 
194     return 0;
195 }