13 树的应用-并查集
Posted Make a commitment to your own
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了13 树的应用-并查集相关的知识,希望对你有一定的参考价值。
昨晚熬夜写出来了 电脑没电了没保存, 描述又要重新打过。。。。
心好累啊
1、并查集基本描述:是一种简单的集合表示
有三种基本操作:
①Union:把S中子集合Root2并入子集合Root1中。
②Find:查找子集合S中单元素所在的子集合,返回子集合的名字
③initial:把集合中每一个元素都初始化为只有一个单元素的子集合
写的时候添加了路径压缩功能:
实际上是把子元素存储的内容直接改向根结点,在访问的时候可以大大提升速度。查阅了一下 这个功能比较多地是与查找函数合并了。在每查找一个结点以后直接按照子元素到根元素的路径修改路径上每一个元素存放的内容,使其直接指向根结点,这样以后访问的时候可以提高效率。
2、并查集的特点:
用树的双亲表示作为存储结构,每个自己和以一棵树来表示。
所有表示子集合的树构成表示全集合的森林,存放在双亲表示数组之中。
3、适用场合:
查阅了一些资料,并查集实际上非常适合用于解决一些判断动态连通性的题目(不许给出具体路径),通过输入点的前后继关系建立集合,通过判断两个点是否同属于同一个组来判断是否属于同一个集合。
4、代码实现
1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 #define SIZE 10 5 int UFset[SIZE]; 6 /*初始化:初始化所有元素集合为0*/ 7 void initial(int s[]) 8 { 9 int i; 10 for(i=0; i<SIZE; i++) 11 { 12 s[i]=-1; 13 } 14 printf("init successful.\\n"); 15 } 16 /*查找:在并查集中查找并返回包含元素x的树的根*/ 17 int Find(int S[],int x) 18 { 19 while(S[x]>=0) 20 x=S[x]; 21 return x; 22 } 23 /*合并:求两个不相交子集合的并集*/ 24 void Union(int S[],int Root1,int Root2) 25 { 26 S[Root2]=Root1; 27 } 28 void showUFSets(int s[]) 29 { 30 int i; 31 printf("|"); 32 for(i=0; i<SIZE; i++) 33 { 34 printf("%d:%d|",i,s[i]); 35 } 36 printf("\\n"); 37 } 38 /*路径压缩:更新整个集合的元素 39 使其在访问的过程中可以直接找到它的根结点…… 40 看到网上有说这个东西就强行写一个加上去先,具体做题的时候可以把这个算法整合到find函数中,一边找一边更新…… 41 */ 42 void ysroad(int s[]) 43 { 44 int father; 45 for(int i=0;i<SIZE;i++) 46 { 47 if(s[i]!=-1){ 48 father=Find(s,i);//找到i元素的根结点 49 s[i]=father; 50 } 51 } 52 } 53 int main() 54 { 55 int r1[SIZE],r2[SIZE]; 56 initial(r1); 57 58 showUFSets(r1); 59 initial(r2); 60 showUFSets(r2); 61 printf("Test of Union"); 62 int father,son; 63 cin>>father; 64 cin>>son; 65 while(son!=0) 66 { 67 r1[son]=father; 68 cout<<"successful"<<endl; 69 cin>>father; 70 cin>>son; 71 } 72 cout<<"before:"<<endl; 73 showUFSets(r1); 74 ysroad(r1); 75 cout<<"after"<<endl; 76 showUFSets(r1); 77 return 0; 78 }
5、代码实现截图
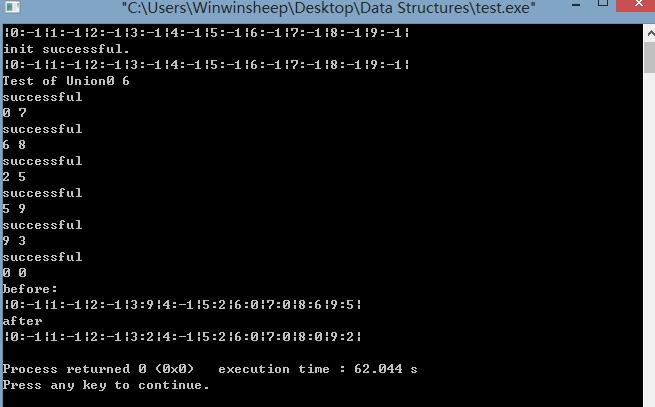
以上是关于13 树的应用-并查集的主要内容,如果未能解决你的问题,请参考以下文章