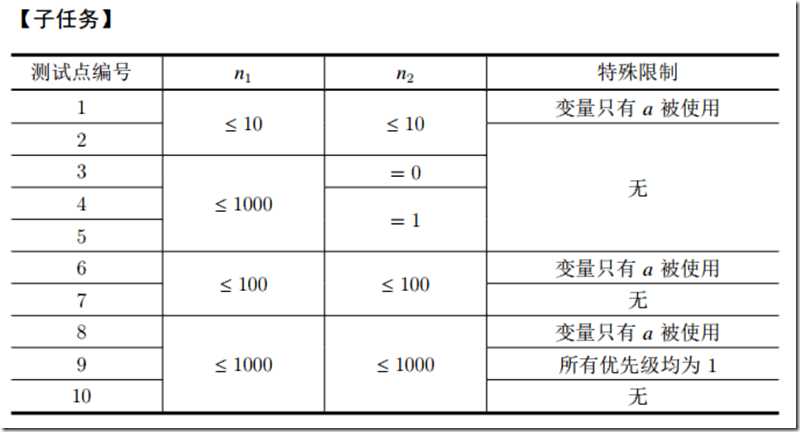
XJOI 并行程序(概率DP)

Posted 2020-10-06

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了XJOI 并行程序(概率DP)相关的知识，希望对你有一定的参考价值。

zrf的第三题,对本蒟蒻来说完全不可做.考试后苦逼地调了7个小时才调出来,论我有多意识模糊……

那么这题就是一个概率dp

f[i][j][k]表示第一个程序执行到i行,第二个程序执行到j行,第k个变量的期望

g[i][j]表示第一个程序执行到i行,第二个程序执行到j行的期望

愉快的写12个转移(怎么会是愉快的呢?QAQ)

即可.

#include<map>
#include<cstdio>
#include<string>
#include<iostream>
using namespace std;
typedef long long ll;
const int M=1e9+7,N=1010;
struct senten{
    int y,x,z,ind;
}a[2][N];
int prep[2][N],n[2];
ll f[N][N][26],g[N][N],fp[11],tmp[26],ans[N];
inline int rate(int x,int y){
    return fp[y]*x%M;
}
void readme(){
    string s;
    char kk,kke;
    map<string,int>mp;
    mp["MOV1"]=1; mp["MOV2"]=2; mp["ADD"]=3; mp["SUB"]=4; mp["MUL"]=5; mp["PRINT"]=6;
    fp[1]=1; for (int i=2; i<=10; i++) fp[i]=fp[M%i]*(M-M/i)%M;
    ios::sync_with_stdio(false);
    for (int i=0; i<2; i++){
        cin>>n[i];
        for (int j=1; j<=n[i]; j++){
            cin>>a[i][j].y>>s>>kke;
            a[i][j].x=kke-‘a‘;
            switch (mp[s]){
                case 1:{
                    a[i][j].ind=1;
                    cin>>kk;
                    a[i][j].z=kk-‘a‘;
                    break;
                }
                case 2:{
                    a[i][j].ind=2;
                    cin>>a[i][j].z;
                    break;
                }
                case 3:{
                    a[i][j].ind=3;
                    cin>>kk;
                    a[i][j].z=kk-‘a‘;
                    break;
                }
                case 4:{
                    a[i][j].ind=4;
                    cin>>kk;
                    a[i][j].z=kk-‘a‘;
                    break;
                }
                case 5:{
                    a[i][j].ind=5;
                    cin>>a[i][j].z;
                    break;
                }
                case 6:{
                    a[i][j].ind=6;
                    prep[i][j]++;
                    break;
                }
            }
            prep[i][j]+=prep[i][j-1];
        }
    }
}
void dp(){
    g[0][0]=1;
    for (int i=0; i<=n[0]; i++)
    for (int j=0; j<=n[1]; j++){
        ll le=rate(a[0][i].y,a[0][i].y+a[1][j+1].y);
        ll ri=rate(a[1][j].y,a[0][i+1].y+a[1][j].y);
        if (i) g[i][j]=(g[i][j]+g[i-1][j]*rate(a[0][i].y,a[0][i].y+a[1][j+1].y)%M)%M;
        if (j) g[i][j]=(g[i][j]+g[i][j-1]*rate(a[1][j].y,a[0][i+1].y+a[1][j].y)%M)%M;
        if (i){
            for (int k=0; k<26; k++) tmp[k]=f[i-1][j][k];
            if (a[0][i].ind==1) tmp[a[0][i].x]=tmp[a[0][i].z];
            else if (a[0][i].ind==2) tmp[a[0][i].x]=g[i-1][j]*a[0][i].z%M;
            else if (a[0][i].ind==3) (tmp[a[0][i].x]+=tmp[a[0][i].z])%=M;
            else if (a[0][i].ind==4) (tmp[a[0][i].x]+=M-tmp[a[0][i].z])%=M;
            else if (a[0][i].ind==5) (tmp[a[0][i].x]*=a[0][i].z)%=M;
            else if (a[0][i].ind==6) (ans[prep[0][i]+prep[1][j]]+=tmp[a[0][i].x]*le%M)%=M;
            for (int k=0; k<26; k++) f[i][j][k]=tmp[k]*le%M;
        }
        if (j){
            for (int k=0; k<26; k++) tmp[k]=f[i][j-1][k];
            if (a[1][j].ind==1) tmp[a[1][j].x]=tmp[a[1][j].z];
            else if (a[1][j].ind==2) tmp[a[1][j].x]=g[i][j-1]*a[1][j].z%M;
            else if (a[1][j].ind==3) (tmp[a[1][j].x]+=tmp[a[1][j].z])%=M;
            else if (a[1][j].ind==4) (tmp[a[1][j].x]+=M-tmp[a[1][j].z])%=M;
            else if (a[1][j].ind==5) (tmp[a[1][j].x]*=a[1][j].z)%=M;
            else if (a[1][j].ind==6) (ans[prep[0][i]+prep[1][j]]+=tmp[a[1][j].x]*ri%M)%=M;
            for (int k=0; k<26; k++) (f[i][j][k]+=tmp[k]*ri%M)%=M;
        }
    }
}
void print(){
    for (int i=1; i<=prep[0][n[0]]+prep[1][n[1]]; i++) cout<<ans[i]<<" ";
}
int main(){
    readme();
    dp();
    print();
}