hdu 6198（矩阵快速幂）

Posted 2020-10-06 见字如面

number number number

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 175    Accepted Submission(s): 119

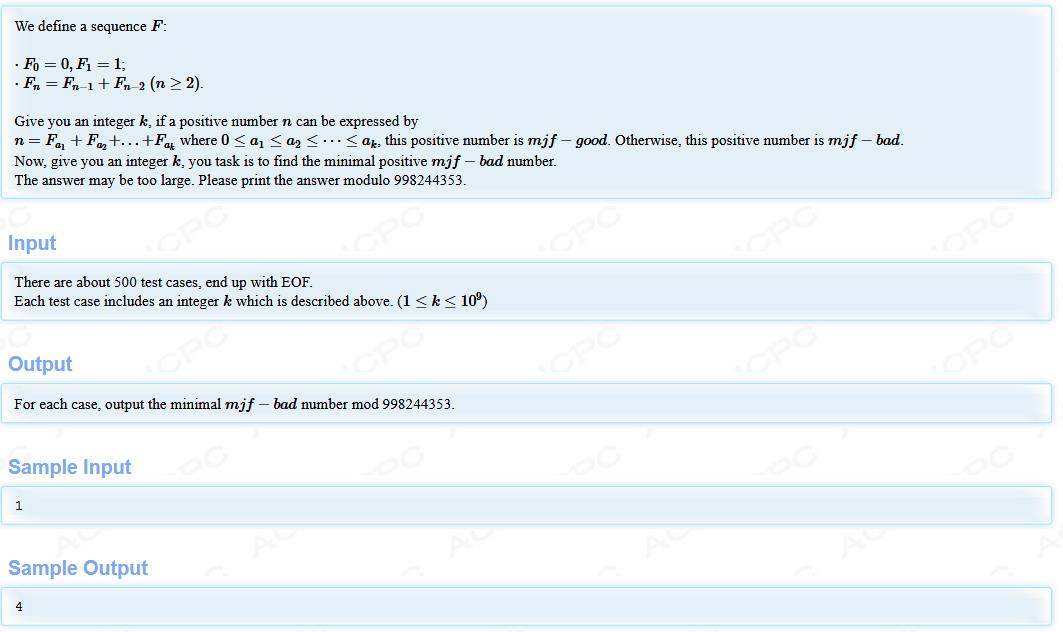
暴力发现当4 12 33 88 232

和斐波那契数列对比  答案为 第2*k+3个数减1

直接用矩阵快速幂求的F[2*k+3]  然后减1

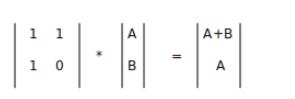A=1,B=0;

然后矩阵快速幂2*k+3-1次得到F[2*k+3]

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<string.h>
 7 #include<map>
 8 #include<set>
 9 #include<queue>
10 #include<vector>
11 #include<cstdlib>
12 typedef long long ll;
13 typedef unsigned long long LL;
14 using namespace std;
15 const int INF=0x3f3f3f3f;
16 const int num=100;
17 const int mod=998244353;
18 int N;
19 struct Mat{
20     ll a[num][num];
21     void init(){
22         memset(a,0,sizeof(a));
23         for(int i=0;i<num;i++)
24             a[i][i]=1;
25     }
26 };
27 Mat mul(Mat a,Mat b){
28     Mat ans;
29     for(int i=0;i<N;i++){
30     for(int j=0;j<N;j++){
31         ans.a[i][j]=0;
32         for(int k=0;k<N;k++){
33             ans.a[i][j]+=a.a[i][k]*b.a[k][j];
34         }
35         ans.a[i][j]=ans.a[i][j]%mod;
36     }
37     }
38     return ans;
39 }
40 Mat power(Mat a,int n){
41     Mat ans;
42     ans.init();
43     while(n){
44         if(n&1){
45             ans=mul(ans,a);
46         }
47         n=n>>1;
48         a=mul(a,a);
49     }
50     return ans;
51 }
52 int main(){
53     int k;
54     N=2;
55     while(scanf("%d",&k)!=EOF){
56         k=k*2+3;
57         Mat aa;
58         aa.a[0][0]=1;
59         aa.a[0][1]=1;
60         aa.a[1][0]=1;
61         aa.a[1][1]=0;
62         Mat ans=power(aa,k-1);
63         ll t=((ans.a[0][0]-1)%mod+mod)%mod;
64         cout<<t<<endl;
65     }
66     return 0;
67 }