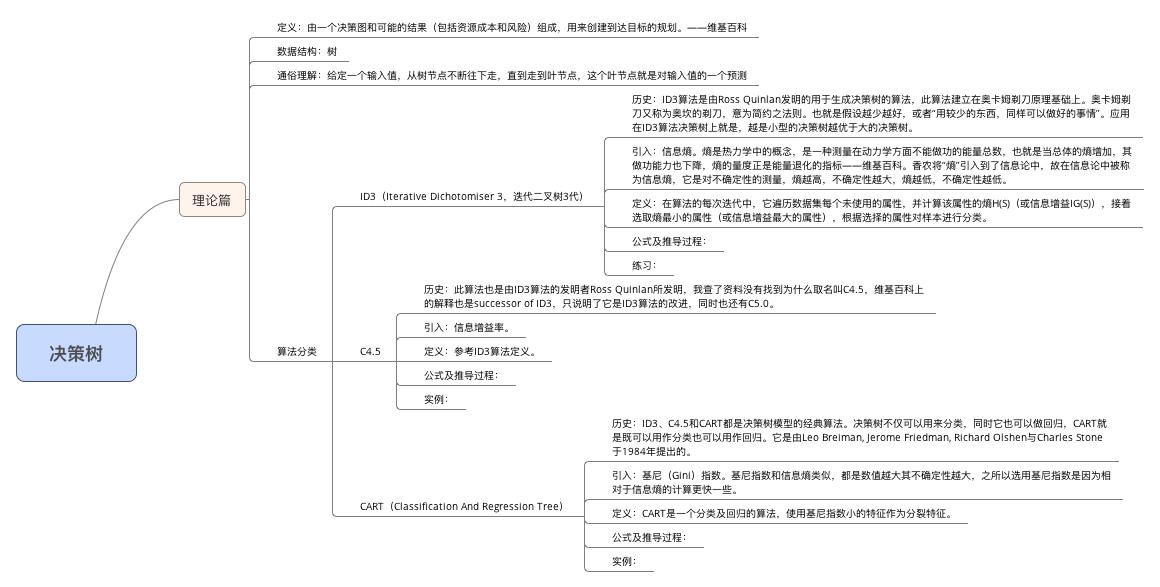
决策树（理论篇）

Posted 2020-10-06 CoderBuff

 

定义

　　由一个决策图和可能的结果（包括资源成本和风险组成），用来创建到达目的的规划。——维基百科

通俗理解

　　给定一个输入值，从树节点不断往下走，直至走到叶节点，这个叶节点就是对输入值的一个预测或者分类。

算法分类

ID3（Iterative Dichotomiser 3，迭代二叉树3代）

历史

　　ID3算法是由Ross Quinlan发明的用于生成决策树的算法，此算法建立在奥卡姆剃刀上。奥卡姆剃刀又称为奥坎的剃刀，意为简约之法则，也就是假设越少越好，或者“用较少的东西，同样可以做好的事情”，即越是小型的决策树越优于大的决策树。当然ID3它的目的并不是为了生成越小的决策树，这只是这个算法的一个哲学基础。

引入

　　信息熵。熵是热力学中的概念，是一种测量在动力学方面不能做功的能量总数，也就是当总体熵的增加，其做功能力也下降，熵的量度正是能量退化的指标——维基百科。香农将“熵”的概念引入到了信息论中，故在信息论中被称为信息熵，它是对不确定性的测量，熵越高，不确定性越大，熵越低，不确定性越低。

　　那么到底何为“信息熵”？它是衡量信息量的一个数值。那么何又为“信息量”？我们常常听到某段文字信息量好大，某张图信息量好大，实际上指的是这段消息（消息是信息的物理表现形式，信息是其内涵——《通信原理》）所包含的信息很多，换句话说传输信息的多少可以采用“信息量”去衡量。这里的消息和信息并不完全对等，有可能出现消息很大很多，但所蕴含有用的信息很少，也就是我们常说的“你说了那么多（消息多），但对我来说没用（信息少，即信息量少）”。这也进一步解释了消息量的定义是传输信息的多少。

　　进一步讲，什么样的消息才能构成信息呢？

　　我们为什么会常常发出感叹“某段文字的信息量好大”，得到这条消息时是不是有点出乎你的意料呢？比如，X男和X男在同一张床上发出不可描述的声音，这段消息对于你来讲可能就会发出“信息量好大”的感叹。再比如，某情侣在同一张床上发出不可描述的声音，这段消息对于你来讲可能就是家常便饭，并不会发出“信息量好大”的感叹。前一个例子的消息中所构成的信息很大，后一个例子的消息中所构成的信息很小，这是因为，只有消息中不确定的内容才构成的消息才构成信息。消息所表达的事件越不可能发生，越不可预测，就会越使人感到惊讶和意外，信息量就越大——《通信原理》。

　　我们解释了消息、信息、信息量之间的关系。回到信息熵上来之前，我们还得继续上面的话题，上面提到了“事件发生的可能性”，这很理所当然的是可以以出现的概率来描述，也就是说我们现在更进一步，信息量与消息中事件发生的概率相关，上面的例子就可以这么描述：消息中的事件发生概率越小，信息量越大，消息中的事件发生的概率越大，信息量就越小。

　　而信息熵是接收的每条消息中的包含的信息的平均值，数学上也就是信息量的期望，也就是在结果出来之前对可能产生的信息量的期望。

　　最后小结，如果熵很大，也就是信息量的期望大，也就是事件的概率小，更或者事件的不确定性大。

　　先给出信息熵的公式：，X为随机变量，其值域为{}，其中P为X的概率质量函数。下面我们来逐步推导出这个公式（据《通信原理》）：

1. 非负性。消息中所含信息量就是该消息中的事件所出现的概率：
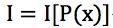
2. 单调性。概率越大，消息量越小，P(x)=1，I=0；P(x)=0，I=∞，完全不可能发生的事情它的信息量就很大很大，例如太阳西边生气了这种事情。

3. 累加性。若干个相互独立事件构成的消息，所含信息量等于各独立事件消息量之和，消息量具有可加性：

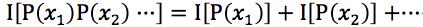
4.  综上，满足以上三个性质的公式,香农将信息量定义为：

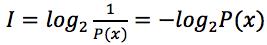
5.  信息熵是信息量的期望，也就是，离散型随机变量的期望也即是统计平均值，是试验中每次可能的结果乘以其结果概率的综合，那么

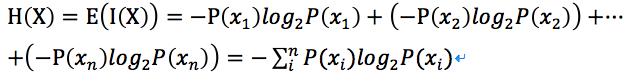
定义

　　在引入了信息熵这个概念后，接着开始正式介绍ID3算法。在算法的每次迭代中，它遍历数据集每个未使用的属性，并计算该属性的熵H(S)（或信息增益IG(S)），接着选取熵最小的属性（或信息增益最大的属性），根据选择的属性对样本进行分类。（On each iteration of the algorithm, it iterates through every unused attribute of the set S and calculates the entropy H(S) (or information gain IG(S)) of that attribute. It then selects the attribute which has the smallest entropy (or largest information gain) value. The set S}is then split by the selected attribute (e.g. age is less than 50, age is between 50 and 100, age is greater than 100) to produce subsets of the data.——wikipekia）对于ID3，实际上是计算信息熵的一个过程，选择信息熵最低的属性或者称为特征，当然通常是计算信息增益，下面给出公式及推导过程。

公式及推导过程

　　信息增益：IG(A) = H(D) – H(D|A)。D表示样本集，A表示属性（或特征），IG(A)表示特征A的信息增益，H(D)表示样本的信息熵，H(D|A)表示特征A对样本集D的经验条件熵（即条件概率分布）。
　　信息熵在前面已经介绍过，对于经验条件熵，只需回顾一下条件概率分布。
　　对于离散型随机变量X和Y，随机变量Y在条件{X = x}下的条件概率分别是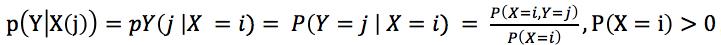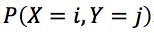：，表示X和Y的联合分布概率，即“X=i，并且Y=j发生的概率”，这是数学公式。

　　对于条件熵H(Y|X=x)为变数Y在变数X取特定值x条件下的熵，那么H(Y|X)就是H(Y|X=x)在X取遍所有x后平均的结果。那么可得出以下公式推导：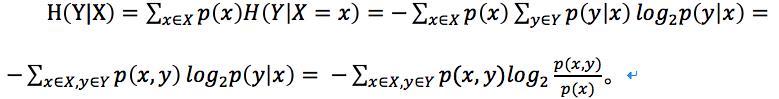

　　整个推导过程和条件概率分布公式息息相关。
　　最后也即得出信息增益的公式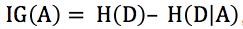：，代入即可。

　　给出《机器学习》中的公式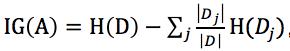：，其中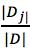充当第j个分区的权重。

练习

 　　一共有14个样本数据D，且有年龄、收入、是否是学生、信用评级4个特征，分类为是否可能购买电脑。计算样本数据的信息熵以及各个特征的信息增益。

　　根据信息熵公式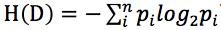：可得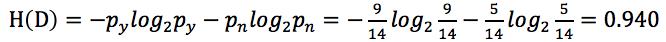：（py表示购买电脑的概率，pn表示不购买电脑的概率）

　　接下来计算年龄的条件熵：

　　其中低年龄占5/14，且购买电脑占2/5，不能购买电脑占3/5； 

　　中年龄占4/14，且购买电脑占4/4，不能购买电脑占0/4；
　　高年龄占5/14，且购买电脑占3/5，不能购买电脑占2/5。

 　　根据条件熵的计算公式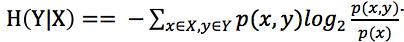：可得：

　　关于条件熵这里要再多加解释一下公式，在本例中X表示年龄且X={低，中，高}，也就是说X要取完这三个值，在这三个值的条件确定下Y的条件熵，而Y表示是否购买电脑且Y={是，否}，换算成公式即是：。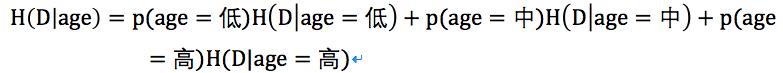

　　上面我们已经计算过，H(D)=0.94那么：

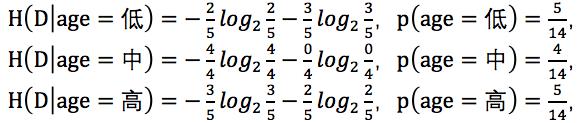
　　可得：

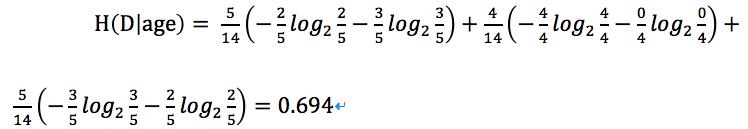
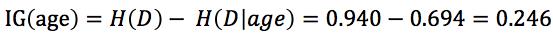　　，依次计算出每个特征的信息增益，选取信息增益最大的特征作为分裂特征。接着再递归计算信息增益形成一棵树决策树。

C4.5

历史

　　此算法也是由ID3算法的发明者Ross Quinlan所发明，我查了资料没有找到为什么取名叫C4.5，维基百科上的解释也是successor of ID3，只说明了它是ID3算法的改进，同时也还有C5.0。

引入

　　信息增益率。既然是ID3算法的改进，那说明它们既有相同点也有不同点，相同点就是同样是基于信息熵，不同点就是ID3使用的是信息增益来作为选择分裂特征，而C4.5使用的则是信息增益率。
　　之所以会有ID3的改进，是因为ID3使用信息增益时如果某个特征数目较多很有可能对此特征有所偏好，改用信息增益率就会减少这种影响。
　　在前面我们介绍了信息熵以及信息增益，那么什么又是信息增益率呢？信息增益率使用一个叫做“分裂信息”值将信息增益规范化，分类信息的公式为：

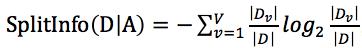，和信息增益有点类似。

定义

　　C4.5同ID3类似，不同的只是选择分裂特征的方式不同，C4.5引入的是“信息增益率”来选择，选择信息增益率大的特征，参考ID3算法定义。

公式及推导过程

　　上面引入了信息增益率，开头我们提到了C4.5不直接只用“信息增益”来选择分裂特征，而是通过“信息增益率”，而信息增益率是在信息增益的基础上除以分类信息。

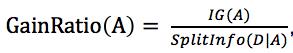　　，信息增益IG(A)以及分裂信息SplitInfo(D|A)均已给出，此处不再重复。

练习

　　还是ID3中的例子，在ID3的例子中我们已经计算了特征为age时的信息增益，我们只需再计算出特征age的分裂属性即可。

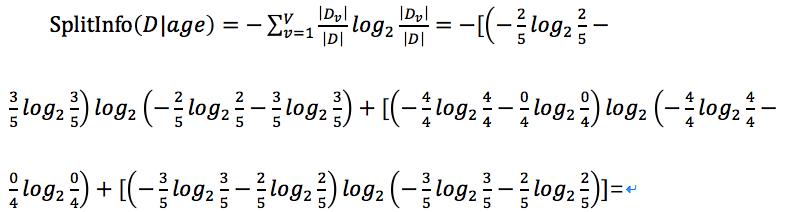
　　当然增益率就根据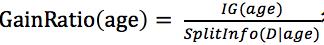得出。

　　具体数值以及其他特征的增益率不再给出，选择增益率最大的特征。

CART(Classification and Regression Trees，分类回归树)

历史

　　ID3、C4.5和CART都是决策树模型的经典算法。决策树不仅可以用来分类，同时它也可以做回归，CART就是既可以用作分类也可以用作回归。它是由Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出的。

引入

　　基尼（Gini）指数。与ID3和C4.5通过信息熵来确定分裂特征不同，CART通过一个叫基尼指数的东西来确定分裂特征。
　　在经济学中也有一个基尼系数（或基尼指数），我暂时未找到这两者之间有没有什么联系，或者这里的基尼指数是否引自经济学。
　　基尼指数和信息熵类似，都是数值越大其不确定性越大，之所以选用基尼指数是因为相对于信息熵的计算更快一些。

定义

　　CART是一个分类及回归的算法，使用基尼指数小的特征作为分裂特征。

公式及推导过程

　　CART算法其核心公式就是基尼指数的计算，基尼指数越大不确定越大，基尼指数的计算公式为：

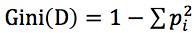　　，其中pi是D中元组中Ci类的概率。

练习

　　现在有10个样本，其中有是否有房、婚姻状况、年收入3个特征，根据这三个特征来判断是否拖欠贷款。

　　先选取是否有房这个特征来计算它的基尼指数。

　　可知有房者占3/10，其中未拖欠贷款占3/3，拖欠贷款占0/3;
　　无房者占7/10，其中未拖欠贷款占4/7，拖欠贷款占3/7;

　　有房者的基尼指数记为;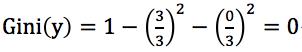

　　无房者的基尼指数记为;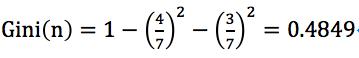

　　是否有房的基尼指数为。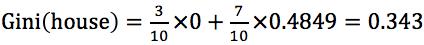

　　以此计算各个特征的基尼指数，选取最小的作为分裂特征。

---

　　机器学习中有关决策树相关的理论方面大致已经介绍完毕，实际上是主要介绍了ID3、C4.5、CART三种算法，对于决策树并没有很详尽的理论讲解，例如构造过程剪枝等。在后面对决策树的学习中随时再来舔砖加瓦，也请看到此篇博客的朋友能给予指点。