机器学习:特征工程
Posted 兔子爱读书
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习:特征工程相关的知识,希望对你有一定的参考价值。
特征选择直接影响模型灵活性、性能及是否简洁。
好特征的灵活性在于它允许你选择不复杂的模型,同时运行速度也更快,也更容易理解和维护。
特征选择
四个过程:产生过程,评价函数,停止准则,验证过程。
目的:过滤特征集合中不重要特征,挑选一组最具统计意义的特征子集,从而达到降维的效果。
选择标准:特征项和类别项之间的相关性(特征重要性)。
- - -搜索特征子空间的产生过程- - -
搜索的算法分为完全搜索(Complete),启发式搜索(Heuristic), 随机搜索(Random) 3大类。
完全搜索包括(4种):广度优先搜索(穷举法)、分支限界搜索(穷举法+剪枝)、 定向搜索(选择TopN)、最优优先搜索(TopN问题不限制N)
启发式搜索包括(6种):
序列前向选择SFS(简单贪心,每次选使评价函数达到最优的特征)、序列后向选择SBS(简单贪心,每次剔除特征)、 双向搜索BDS(SFS与SBS同时开始,碰撞时结束);
增L去R选择算法 LRS(空集开始先加L后去R、全集开始先去R后加L)、序列浮动选择(LRS法不固定L与R)、决策树搜索(让树充分生长、然后剪枝,通过信息熵评价)
随机算法搜索(3种):随机产生序列选择算法RGSS(随机产生特征子集,运行SFS或SBS)、模拟退火算法SA(克服序列搜索局部最优、但最优解区域很小时不适用)、遗传算法GA(随机产生特征子集,评分,然后交叉、突变等繁衍出下一代特征子集)
- - - - 特征选择与评价函数 - - - -
评价函数的作用是评价产生过程所提供的特征子集的好坏。
评价函数根据其工作原理,主要分为筛选器(Filter)、封装器( Wrapper )两大类。
封装器实质上是一个分类器,封装器用选取的特征子集对样本集进行分类,分类的错误率作为衡量特征子集好坏的标准。
筛选器通过分析特征子集内部的特点来衡量其好坏。筛选器一般用作预处理,与分类器的选择无关。特征选择法主要指筛选器的选择方法。
筛选器选择特征:
预处理:首先去掉取值变化小的特征(对系统影响最小、最不重要的特征),接下来有四种方法:
单变量的特征选择方法、基于机器学习模型的选择法、随机森林法、顶层特征选择法(基于不同的模型选择法)
1.单变量的特征选择方法
独立地衡量每个特征与响应变量之间的关系,分为两大类:
基于距离计算的特征选择——Pearson相关系数,Gini-index(基尼指数),IG(信息增益)、常规距离公式;
基于树与交叉验证的特征选择法——适用于非线性关系。
(1) Pearson相关系数
按照大学的线性数学水平来理解, 它可以看做是两组数据的向量夹角的余弦。
皮尔逊相关的约束条件:两变量独立、两个变量间有线性关系、变量是连续变量、均符合正态分布且二元分布也符合正态分布。



评价:
Pearson相关系数结果取值区间为[-1,1],-1表示完全的负相关(这个变量下降,那个就会上升),+1表示完全的正相关,0表示没有线性相关。
优点:速度快、易于计算,经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。
缺点:只对线性关系敏感。如果关系是非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近0。
(2) Gini-index(基尼指数)
系统信息熵:
条件熵(指特征X被固定为值xi时):
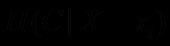
条件熵(指特征X被固定时):

信息增益:
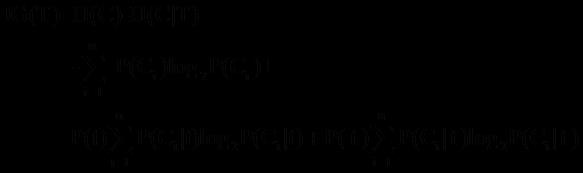
(4) 常规距离公式 (Distance Metrics )
运用距离度量进行特征选择是基于这样的假设:好的特征子集应该使得属于同一类的样本距离尽可能小,属于不同类的样本之间的距离尽可能远。
常用的距离度量(相似性度量)包括欧氏距离、标准化欧氏距离、马氏距离等。
(5) 基于树与交叉验证的特征选择法
假如某个特征和响应变量之间的关系是非线性的,可以用基于树的方法(决策树、随机森林)、交叉验证、扩展的线性模型等。
基于树的方法比较易于使用,因为他们对非线性关系的建模比较好,并且不需要太多的调试。但要注意过拟合问题,因此树的深度最好不要太大。
2.基于机器学习模型的选择法
有些机器学习方法本身就具有对特征进行打分的机制,或者很容易将其运用到特征选择任务中,例如回归模型,SVM,决策树,随机森林等等。
在一些地方叫做wrapper类型,大意是,特征排序模型和机器学习模型是耦盒在一起的,对应的非wrapper类型的特征选择方法叫做filter类型。
例如在回归模型中利用的系数来选择特征。越是重要的特征在模型中对应的系数就会越大,而跟输出变量越是无关的特征对应的系数就会越接近于0。在噪音不多的数据上,或者是数据量远远大于特征数的数据上,如果特征之间相对来说是比较独立的,那么即便是运用最简单的线性回归模型也一样能取得非常好的效果。同样的方法和套路可以用到类似的线性模型上,比如逻辑回归。
正则化模型:就是把额外的约束或者惩罚项加到已有模型(损失函数)上,以防止过拟合并提高泛化能力。损失函数由原来的E(X,Y)变为E(X,Y)+alpha||w||,w是模型系数组成的向量(有些地方也叫参数parameter,coefficients),||·||一般是L1或者L2范数,alpha是一个可调的参数,控制着正则化的强度。当用在线性模型上时,L1正则化和L2正则化也称为Lasso和Ridge。
3. 随机森林
随机森林具有准确率高、鲁棒性好、易于使用等优点,这使得它成为了目前最流行的机器学习算法之一。
随机森林提供了两种特征选择的方法:平均不纯度减少、平均精确率减少。
(1) 平均不纯度减少 (mean decrease impurity)
随机森林由多个决策树构成。决策树中的每一个节点都是关于某个特征的条件,为的是将数据集按照不同的响应变量一分为二。利用不纯度可以确定节点(最优条件),对于分类问题,通常采用基尼不纯度或者信息增益,对于回归问题,通常采用的是方差或者最小二乘拟合。当训练决策树的时候,可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说,可以算出每个特征平均减少了多少不纯度,并把它平均减少的不纯度作为特征选择的值。
使用基于不纯度的方法的时候,要注意:
1、这种方法存在偏向,对具有更多类别的变量会更有利;
2、对于存在关联的多个特征,其中任意一个都可以作为指示器(优秀的特征),并且一旦某个特征被选择之后,其他特征的重要度就会急剧下降,因为不纯度已经被选中的那个特征降下来了,其他的特征就很难再降低那么多不纯度了,这样一来,只有先被选中的那个特征重要度很高,其他的关联特征重要度往往较低。在理解数据时,这就会造成误解,导致错误的认为先被选中的特征是很重要的,而其余的特征是不重要的,但实际上这些特征对响应变量的作用确实非常接近的(这跟Lasso是很像的)。
特征随机选择方法稍微缓解了这个问题,但总的来说并没有完全解决。
(2) 平均精确率减少 (Mean decrease accuracy)
主要思路是直接度量每个特征对模型精确率的影响,通过打乱每个特征的特征值顺序,来度量顺序变动对模型的精确率的影响。
很明显,对于不重要的变量来说,打乱顺序对模型的精确率影响不会太大,但是对于重要的变量来说,打乱顺序就会降低模型的精确率。
4. 两种顶层特征选择算法
之所以叫做顶层,是因为他们都是建立在基于模型的特征选择方法基础之上的,例如回归和SVM,在不同的子集上建立模型,然后汇总最终确定特征得分。
有两种方法:稳定性选择 (Stability selection);递归特征消除RFE (Recursive feature elimination)
稳定性选择是一种基于二次抽样和选择算法相结合较新的方法,选择算法可以是回归、SVM或其他类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法,不断的重复,最终汇总特征选择结果。比如可以统计某个特征被认为是重要特征的频率(被选为重要特征的次数除以它所在的子集被测试的次数)。理想情况下,重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数,而最无用的特征得分将会接近于0。
递归特征消除的主要思想是反复的构建模型(如SVM或者回归模型)然后选出最好的(或者最差的)的特征(可以根据系数来选),把选出来的特征放到一遍,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。因此,这是一种寻找最优特征子集的贪心算法。
- - - - 过滤器方法的简单比较 - - - -
Lasso能够挑出一些优质特征,同时让其他特征的系数趋于0。当如需要减少特征数的时候它很有用,但是对于数据理解来说不是很好用。(例如在结果中,X11,X12,X13的得分都是0,好像他们跟输出变量之间没有很强的联系,但实际上不是这样的)
MIC对特征一视同仁,这一点上和关联系数有点像。另外,它能够找出X3和响应变量之间的非线性关系。
随机森林基于不纯度的排序结果非常鲜明。在得分最高的几个特征之后的特征,得分急剧的下降。从表中可以看到,得分第三的特征比第一的小4倍。而其他的特征选择算法就没有下降的这么剧烈。
Ridge将回归系数均匀的分摊到各个关联变量上,从表中可以看出,X11,…,X14和X1,…,X4的得分非常接近。
稳定性选择常常是一种既能够有助于理解数据又能够挑出优质特征的这种选择。像Lasso一样,它能找到那些性能比较好的特征(X1,X2,X4,X5),同时,与这些特征关联度很强的变量也得到了较高的得分。
参考资料:
干货:结合Scikit-learn介绍几种常用的特征选择方法
以上是关于机器学习:特征工程的主要内容,如果未能解决你的问题,请参考以下文章
![clip_image002[4] 技术分享](https://image.cha138.com/20200630/6c9bcfef960b4918afa4426447945562.jpg)