BZOJ4817 SDOI2017 相关分析

Posted 2020-10-06

4821: [Sdoi2017]相关分析

Time Limit: 10 Sec  Memory Limit: 128 MBSec  Special Judge

Description

Frank对天文学非常感兴趣，他经常用望远镜看星星，同时记录下它们的信息，比如亮度、颜色等等，进而估算出

星星的距离，半径等等。Frank不仅喜欢观测，还喜欢分析观测到的数据。他经常分析两个参数之间（比如亮度和

半径）是否存在某种关系。现在Frank要分析参数X与Y之间的关系。他有n组观测数据，第i组观测数据记录了x_i和

y_i。他需要一下几种操作1 L,R：用直线拟合第L组到底R组观测数据。用xx表示这些观测数据中x的平均数，用yy

表示这些观测数据中y的平均数，即

xx=Σx_i/(R-L+1)(L<=i<=R)

yy=Σy_i/(R-L+1)(L<=i<=R)

如果直线方程是y=ax+b，那么a应当这样计算：

a=(Σ(x_i-xx)(y_i-yy))/(Σ(x_i-xx)(x_i-xx)) (L<=i<=R)

你需要帮助Frank计算a。

2 L,R,S,T：

Frank发现测量数据第L组到底R组数据有误差，对每个i满足L <= i <= R，x_i需要加上S，y_i需要加上T。

3 L,R,S,T：

Frank发现第L组到第R组数据需要修改，对于每个i满足L <= i <= R，x_i需要修改为(S+i)，y_i需要修改为(T+i)。

Input

第一行两个数n,m，表示观测数据组数和操作次数。

接下来一行n个数，第i个数是x_i。

接下来一行n个数，第i个数是y_i。

接下来m行，表示操作，格式见题目描述。

1<=n,m<=10^5,0<=|S|,|T|,|x_i|,|y_i|<=10^5

保证1操作不会出现分母为0的情况。

Output

对于每个1操作，输出一行，表示直线斜率a。

选手输出与标准输出的绝对误差不超过10^-5即为正确。

Sample Input

3 5
1 2 3
1 2 3
1 1 3
2 2 3 -3 2
1 1 2
3 1 2 2 1
1 1 3

Sample Output

1.0000000000
-1.5000000000
-0.6153846154

 

　　本来我是不会想起这道题的。但是有这么一个故事：

　　开学，学科，数学课，变量的相关性。

　　下课后，同学们聚在一起搞事。

　　QT：“你记不记得SDOI2017 D2T3 相关分析？”

　　我：“……蛤？”

　　QT：“题目没给你化简，数学书上化简了。”

　　我：“……蛤？”

　　QT：“拆开式子之后有4个东西要维护，我不会(想)写。”

　　我：“……蛤？”

　　…………

　　在机房写作业。

　　QT：“不行这个数学作业太难算了，我要编程计算。”

　　Anson：“你可以打一波SDOI2017 相关分析。”

　　QT(虚伪地)：“我不会打。”

　　然而因为我早已从Jesse那里蒯了一个calc.cpp，作业已经写完了。

　　然后我就只是想看看传说中的SDOI2017D2T3是什么题，我是不是忘的一干二净。

　　然后发现果然忘得一干二净。

　　然后就有了下面的事情。

 

　　题解就是显而易见的线段树。

　　把式子拆开看，你就会得到：

 

　　

　　

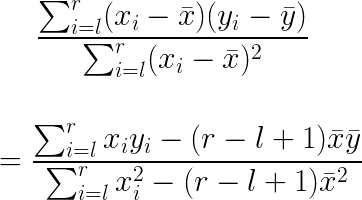
　　上下的后面那一截可以再化简一下。

　　然后就只要维护4个东西：

　　

　　

　　

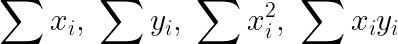
　　这个就很simple了吧，线段树嘛。

　　对于操作2,3，把前后的式子拆一下，维护一下就好了。

　　可以先做codevs的 线段树练习5 思路都是差不多的。

　　思维难度：高中数学。

　　代码难度：MDZZ。

　　PS：这道题就别再codevs交了，它没有SPJ。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob long double
#define ls (x<<1)
#define rs (x<<1|1)
using namespace std;

const int N = 400010;
struct Tree{
  dob x,y,xx,xy;
  Tree operator +(const Tree &t){
    return (Tree){x+t.x,y+t.y,xx+t.xx,xy+t.xy};
  }
}Tr[N*4];
int n,m,lazy_vis[N];
dob X[N/4],Y[N/4],lazy_add1[N],lazy_add2[N],lazy_set1[N],lazy_set2[N];

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)res*=-1;ch=getchar();}
  while(ch<=‘9‘&&ch>=‘0‘)x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline void build(int x,int l,int r){
  if(l==r){
    Tr[x]=(Tree){X[l],Y[l],1.0*X[l]*X[l],1.0*X[l]*Y[l]};
    return;
  }
  int mid=(l+r)>>1;
  build(ls,l,mid);build(rs,mid+1,r);
  Tr[x]=Tr[ls]+Tr[rs];
}

inline dob calc(dob l,dob r){
  return 0.5*(l+r)*(r-l+1);
}

inline dob calcpow(dob l,dob r){
  l-=1;
  dob p1=1.0*(r)*(r+1)*(2*r+1)/6.0;
  dob p2=1.0*(l)*(l+1)*(2*l+1)/6.0;
  return p1-p2;
}

inline void down(int x,int l,int r){
  int mid=(l+r)>>1,sl=mid-l+1,sr=r-mid;
  if(lazy_vis[x]){
    lazy_add1[ls]=lazy_add1[rs]=lazy_add2[ls]=lazy_add2[rs]=0;
    lazy_vis[ls]=lazy_vis[rs]=1;
    dob S=lazy_set1[x],T=lazy_set2[x];
    lazy_set1[ls]=lazy_set1[rs]=lazy_set1[x];
    lazy_set2[ls]=lazy_set2[rs]=lazy_set2[x];
    Tr[ls].xx=1.0*sl*S*S+2.0*S*calc(l,mid)+calcpow(l,mid);
    Tr[rs].xx=1.0*sr*S*S+2.0*S*calc(mid+1,r)+calcpow(mid+1,r);
    Tr[ls].xy=1.0*sl*S*T+1.0*(S+T)*calc(l,mid)+calcpow(l,mid);
    Tr[rs].xy=1.0*sr*S*T+1.0*(S+T)*calc(mid+1,r)+calcpow(mid+1,r);
    Tr[ls].x=1.0*sl*S+calc(l,mid);Tr[rs].x=1.0*sr*S+calc(mid+1,r);
    Tr[ls].y=1.0*sl*T+calc(l,mid);Tr[rs].y=1.0*sr*T+calc(mid+1,r);
    lazy_vis[x]=0;
  }
  if(lazy_add1[x] || lazy_add2[x]){
    dob S=lazy_add1[x],T=lazy_add2[x];
    lazy_add1[ls]+=S;lazy_add1[rs]+=S;
    lazy_add2[ls]+=T;lazy_add2[rs]+=T;
    Tr[ls].xx+=2.0*Tr[ls].x*S+1.0*sl*S*S;
    Tr[rs].xx+=2.0*Tr[rs].x*S+1.0*sr*S*S;
    Tr[ls].xy+=1.0*Tr[ls].x*T+1.0*Tr[ls].y*S+1.0*sl*S*T;
    Tr[rs].xy+=1.0*Tr[rs].x*T+1.0*Tr[rs].y*S+1.0*sr*S*T;
    Tr[ls].x+=1.0*sl*S;Tr[rs].x+=1.0*sr*S;
    Tr[ls].y+=1.0*sl*T;Tr[rs].y+=1.0*sr*T;
    lazy_add1[x]=lazy_add2[x]=0;
  }
}

inline Tree query_1(int x,int l,int r,int xl,int xr){
  if(xl<=l && r<=xr)return Tr[x];
  down(x,l,r);int mid=(l+r)>>1;
  if(xr<=mid)return query_1(ls,l,mid,xl,xr);
  else if(xl>mid)return query_1(rs,mid+1,r,xl,xr);
  return query_1(ls,l,mid,xl,mid)+query_1(rs,mid+1,r,mid+1,xr);
}

inline void update_2(int x,int l,int r,int xl,int xr,dob S,dob T){
  if(xl<=l && r<=xr){
    lazy_add1[x]+=S;lazy_add2[x]+=T;
    Tr[x].xx+=2.0*Tr[x].x*S+1.0*(r-l+1)*S*S;
    Tr[x].xy+=1.0*Tr[x].x*T+1.0*Tr[x].y*S+1.0*(r-l+1)*S*T;
    Tr[x].x+=1.0*(r-l+1)*S;Tr[x].y+=1.0*(r-l+1)*T;
    return;
  }
  down(x,l,r);int mid=(l+r)>>1;
  if(xr<=mid)update_2(ls,l,mid,xl,xr,S,T);
  else if(xl>mid)update_2(rs,mid+1,r,xl,xr,S,T);
  else update_2(ls,l,mid,xl,mid,S,T),update_2(rs,mid+1,r,mid+1,xr,S,T);
  Tr[x]=Tr[ls]+Tr[rs];
}

inline void update_3(int x,int l,int r,int xl,int xr,dob S,dob T){
  if(xl<=l && r<=xr){
    lazy_add1[x]=lazy_add2[x]=0;
    lazy_vis[x]=1;lazy_set1[x]=S;lazy_set2[x]=T;
    Tr[x].xx=1.0*(r-l+1)*S*S+2.0*S*calc(1.0*l,1.0*r)+calcpow(1.0*l,1.0*r);
    Tr[x].xy=1.0*(r-l+1)*S*T+1.0*(S+T)*calc(l,r)+calcpow(l,r);
    Tr[x].x=1.0*(r-l+1)*S+calc(l,r);Tr[x].y=1.0*(r-l+1)*T+calc(l,r);
    return;
  }
  down(x,l,r);int mid=(l+r)>>1;
  if(xr<=mid)update_3(ls,l,mid,xl,xr,S,T);
  else if(xl>mid)update_3(rs,mid+1,r,xl,xr,S,T);
  else update_3(ls,l,mid,xl,mid,S,T),update_3(rs,mid+1,r,mid+1,xr,S,T);
  Tr[x]=Tr[ls]+Tr[rs];
}   

int main()
{
  /*freopen(".in","r",stdin);
    freopen(".out","w",stdout);*/
  n=gi();m=gi();
  for(int i=1;i<=n;++i)X[i]=gi();
  for(int i=1;i<=n;++i)Y[i]=gi();
  build(1,1,n);
  for(int i=1;i<=m;++i){
    int type=gi();
    if(type==1){
      int l=gi(),r=gi();
      Tree ans=query_1(1,1,n,l,r);
      dob fz=ans.xy-ans.x*ans.y/(r-l+1);
      dob fm=ans.xx-ans.x*ans.x/(r-l+1);
      printf("%.10Lf\\n",fz/fm);
    }
    if(type==2){
      int l=gi(),r=gi(),S=gi(),T=gi();
      update_2(1,1,n,l,r,1.0*S,1.0*T);
    }
    if(type==3){
      int l=gi(),r=gi(),S=gi(),T=gi();
      update_3(1,1,n,l,r,1.0*S,1.0*T);
    }
  }
  
  /*fclose(stdin);
    fclose(stdout);*/
  return 0;
}

相关分析