贝叶斯概率论

Posted 2020-10-06 佳星辰

一、贝叶斯定理的形式和解释:

$p(W \\ | \\ D) = \\frac{p(D | W)p(W)}{p(D)}$

它让我们能够通过后验概率p(W | D)，在观测到D之后估计W的不确定性。

贝叶斯定理右侧的量p(D | W)有观测数据集D来估计，可以被看成参数向量W的函数，被称为似然函数(likelihood function)。它表达了在不同参数向量W下，观测数据出现的可能性的大小。注意，似然函数不是w的概率分布，并且它关于w的积分并不一定等于1.

给定似然函数的定义，我们可以用自然语言表述贝叶斯定理：

$postrrior \\propto likelihood \\times prior$ (后验概率 正比于 似然函数和先验概率的乘积)

频率学家广泛使用的一个估计是最大似然估计，其中W的值是使得似然函数p(D | W)达到最大值的W值。这对应于使观察到的数据集出现的概率最大的W的值.

二、高斯分布

对于一元实值变量x，高斯分布被定义为:

$N(x \\ | \\ \\mu,\\sigma ^2) = \\frac{1}{(2\\pi \\sigma ^2)^{\\frac{1}{2}}}exp\\{-\\frac{1}{2\\sigma ^2}(x-\\mu)^2\\}$

它由两个参数控制：u，被叫做均值，以及，被叫做方差。方差的平方根，由给定，被叫做标准差。方差的倒数，记做，被叫做精度。

对于D维向量x的高斯分布定义为

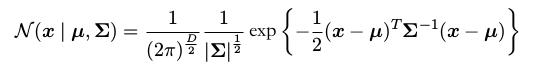
其中D维向量$\\mu$被称为均值，D$\\times$D的矩阵$\\sum$被称为协方差，$|\\sum|$表示$\\sum$的行列式。