2.4 梯度下降算法（非常重要，重点理解）

Posted 2020-10-06 yangzsnews

1. 已经知道了logistic回归模型，
2. 也知道了损失函数
   1. 损失函数是衡量单一训练样例的效果，
3. 还知道了成本函数
   1. 成本函数用于衡量参数w和b的效果在全部训练集上面的衡量
4. 下面开始讨论如何使用梯度下降法来训练或学习训练集上的参数w和b

1. 回顾一下：
   1. 
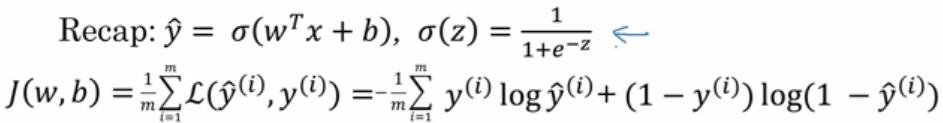
      1. 这里是最熟悉的logistic回归算法
      2. 第二行是成本函数J，成本函数是参数w和b的函数，他被定义为平均值，即1/m的损失函数之和，
      3. 损失函数可以用来衡量你的算法的效果，
         1. 每一个训练样例都会输出y^（i），把它和基本真值标签y（i）进行比较，等号右边展开完全的公式，
      4. 成本函数衡量了参数w和b在训练集上的效果，
         1. 要习得合适的参数w和b，很自然的就想到我们想找到使得成本函数尽可能小的w和b

1. 下面开始来看看梯度下降法
   1. 
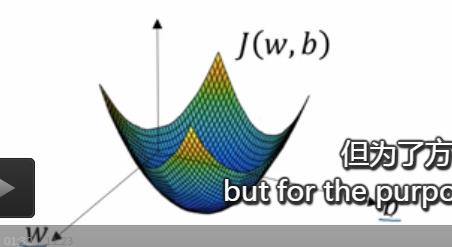
   2. 在这个图中，横轴表示参数w和b，实际中，w可能是高纬度的，但是为了绘图方便，这里让w是一个实数，b也是一个实数，成本函数J(w,b)是在水平轴w和b上的曲面，曲面的高度表示了J(w,b)在某一点的值，
   3. 我们想要做的就是找到这样的w和b使得其对应的成本函数j值是最小值，
   4. 可以看到成本函数J是一个凸函数，
   5. 因此我们的成本函数之所以是凸函数，凸函数这性质是我们使用logistic回归的这个特定的成本函数J的重要原因之一，
   6. 所以为了找到更好的参数值，我们要做的就是利用某个初始值，初始化w和b，用那个小红点表示，
      1. 对于logistic回归而言，几乎是对任意的初始化方法都有效，通常使用0来进行初始化，但是对于logistic回归而言，我们通常不那么做，但是因为函数是凸的，无论在哪里进行初始化，都应该到达同一点，或者是大致相同的点，
   7. 梯度下降所做的就是从初始点开始，朝着最陡的下坡方向走一步，在梯度下降一步后，很有可能停一步，因为他在寻找梯度下降最快的方向，最后可能会找到最终的最优解，
   8. 
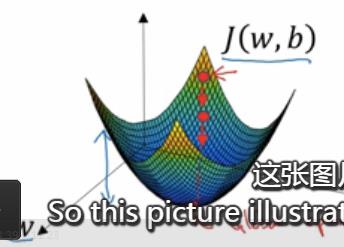
      1. 这张图片阐述了梯度下降法
      2. 下面开始考虑更新w，让w为
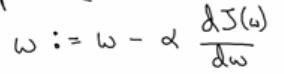
         1. 在算法收敛之前，将会重复这样做，
         2. 这里的阿尔法表示学习率，学习率可以控制每次一次迭代，或者梯度下降法中的步长，之后将会讨论如何选择学习率阿尔法，
         3. 其次，这里面有一个导数，这个就是对参数w的更新或者变化量，
            1. 当我们开始编码，来实现梯度下降，我们会使用代码中变量名的约定dw表示导数，我们使用dw作为导数的变量名，
   9. 现在，我们确保梯度下降法更新是有用的，
      1. 
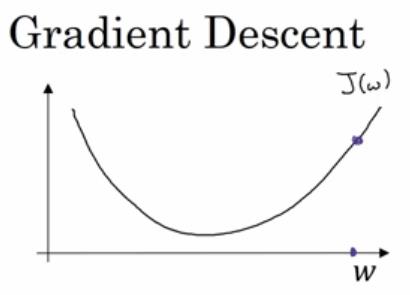
         1. 在横轴上面的一点w和其对应的成本函数J(W)在曲线上的这一点，
         2. 记住导数的定义是函数在这一点的斜率，而函数的斜率是高除以宽，在这个点是一个相切于J(w)的小三角形，
      2. 
         

来自为知笔记(Wiz)