FP-growth算法发现频繁项集——发现频繁项集
Posted 我是8位的
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了FP-growth算法发现频繁项集——发现频繁项集相关的知识,希望对你有一定的参考价值。
上篇介绍了如何构建FP树,FP树的每条路径都满足最小支持度,我们需要做的是在一条路径上寻找到更多的关联关系。
抽取条件模式基
首先从FP树头指针表中的单个频繁元素项开始。对于每一个元素项,获得其对应的条件模式基(conditional pattern base),单个元素项的条件模式基也就是元素项的关键字。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前辍路径(perfix path)。简而言之,一条前缀路径是介于所査找元素项与树根节点之间的所有内容。
下图是以{s:2}或{r:1}为元素项的前缀路径:
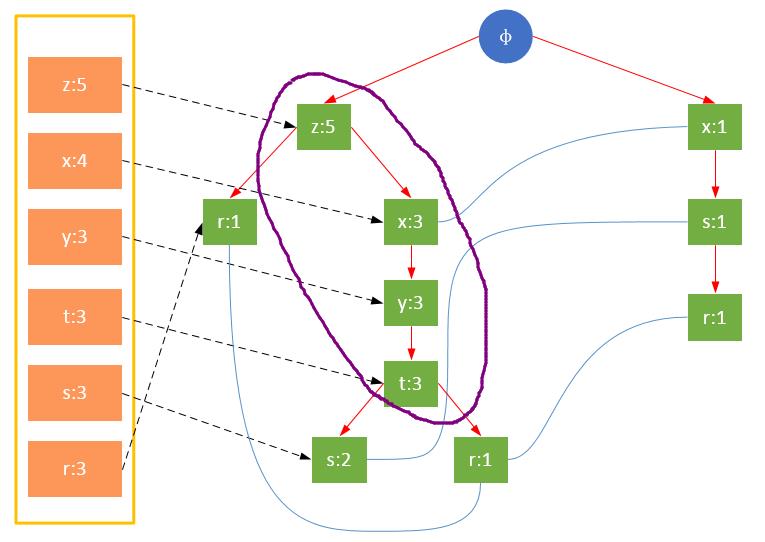
{s}的条件模式基,即前缀路径集合共有两个:{{z,x,y,t}, {x}};{r}的条件模式基共三个:{{z}, {z,x,y,t}, {x,s}}。
寻找条件模式基的过程实际上是从FP树的每个叶子节点回溯到根节点的过程。我们可以通过头指针列表headTable开始,通过指针的连接快速访问到所有根节点。下表是上图FP树的所有条件模式基:

创建条件FP树
为了发现更多的频繁项集,对于每一个频繁项,都要创建一棵条件FP树。可以使用刚才发现的条件模式基作为输入数据,并通过相同的建树代码来构建这些树。然后,递归地发现频繁项、发现条件模式基,以及发现另外的条件树。
以频繁项r为例,构建关于r的条件FP树。r的三个前缀路径分别是{z},{z,x,y,t},{x,s},设最小支持度minSupport=2,则y,t,s被过滤掉,剩下{z},{z,x},{x}。y,s,t虽然是条件模式基的一部分,但是并不属于条件FP树,即对于r来说,它们不是频繁的。如下图所示,y→t→r和s→r的全局支持度都为1,所以y,t,s对于r的条件树来说是不频繁的。

过滤后的r条件树如下:
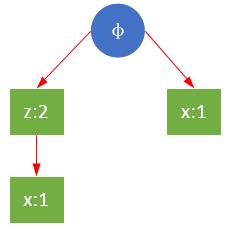
重复上面步骤,r的条件模式基是{z,x},{x},已经没有能够满足最小支持度的路径, 所以r的条件树仅有一个。需要注意的是,虽然{z,x},{x}中共存在两个x,但{z,x}中,z是x的父节点,在构造条件FP树时不能直接将父节点移除,仅能从子节点开始逐级移除。
代码如下:
1 def ascendTree(leafNode, prefixPath): 2 if leafNode.parent != None: 3 prefixPath.append(leafNode.name) 4 ascendTree(leafNode.parent, prefixPath) 5 6 def findPrefixPath(basePat, headTable): 7 condPats = {} 8 treeNode = headTable[basePat][1] 9 while treeNode != None: 10 prefixPath = [] 11 ascendTree(treeNode, prefixPath) 12 if len(prefixPath) > 1: 13 condPats[frozenset(prefixPath[1:])] = treeNode.count 14 treeNode = treeNode.nodeLink 15 return condPats 16 17 def mineTree(inTree, headerTable, minSup=1, preFix=set([]), freqItemList=[]): 18 # order by minSup asc, value asc 19 bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: (p[1][0],p[0]))] 20 for basePat in bigL: 21 newFreqSet = preFix.copy() 22 newFreqSet.add(basePat) 23 freqItemList.append(newFreqSet) 24 # 通过条件模式基找到的频繁项集 25 condPattBases = findPrefixPath(basePat, headerTable) 26 myCondTree, myHead = createTree(condPattBases, minSup) 27 if myHead != None: 28 print(\'condPattBases: \', basePat, condPattBases) 29 myCondTree.disp() 30 print(\'*\' * 30) 31 32 mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) 33 34 simpDat = loadSimpDat() 35 dictDat = createInitSet(simpDat) 36 myFPTree,myheader = createTree(dictDat, 3) 37 myFPTree.disp() 38 condPats = findPrefixPath(\'z\', myheader) 39 print(\'z\', condPats) 40 condPats = findPrefixPath(\'x\', myheader) 41 print(\'x\', condPats) 42 condPats = findPrefixPath(\'y\', myheader) 43 print(\'y\', condPats) 44 condPats = findPrefixPath(\'t\', myheader) 45 print(\'t\', condPats) 46 condPats = findPrefixPath(\'s\', myheader) 47 print(\'s\', condPats) 48 condPats = findPrefixPath(\'r\', myheader) 49 print(\'r\', condPats) 50 51 mineTree(myFPTree, myheader, 2)
控制台信息:
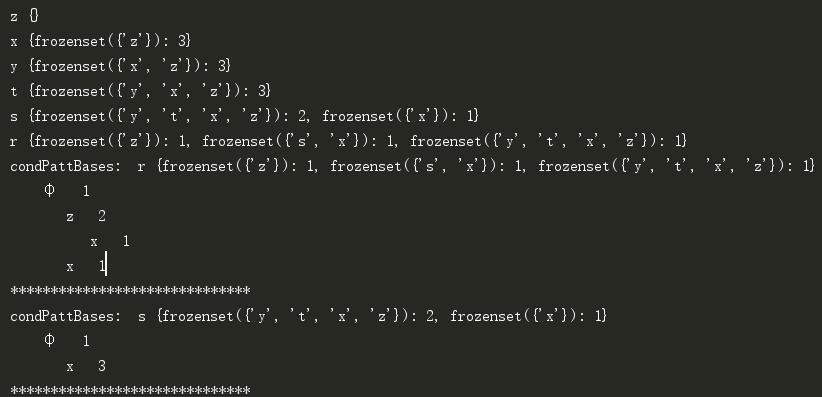
本例可以发现两个频繁项集{z,x}和{x}。
取得频繁项集后,可以根据置信度发现关联规则,这一步较为简单,可参考上篇的相关内容,不在赘述。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”

以上是关于FP-growth算法发现频繁项集——发现频繁项集的主要内容,如果未能解决你的问题,请参考以下文章
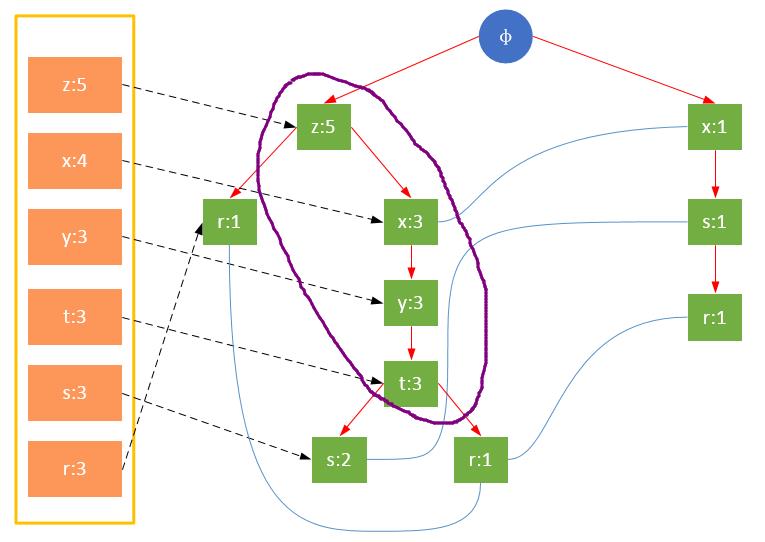 常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FPGrowth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。本文是FP-growth算法的第二篇,主要介绍通过条件FP树发现频繁项集
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FPGrowth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。本文是FP-growth算法的第二篇,主要介绍通过条件FP树发现频繁项集