tyvj——P3524 最大半连通子图
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了tyvj——P3524 最大半连通子图相关的知识，希望对你有一定的参考价值。
描述
输入格式
第一行包含两个整数N，M，X。N，M分别表示图G的点数与边数，X的意义如上文所述。接下来M行，每行两个正整数a, b，表示一条有向边(a, b)。图中的每个点将编号为1,2,3…N，保证输入中同一个(a,b)不会出现两次。
输出格式
应包含两行，第一行包含一个整数K。第二行包含整数C Mod X.
测试样例1
输入
6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4
输出
3
3
备注
对于20%的数据， N ≤18；
对于60%的数据， N ≤10000；
对于100%的数据， N ≤100000, M ≤1000000；
对于100%的数据， X ≤10^8。
最开始的时候没有考虑到有环的时候，他可以连续跑，就没有进行缩点，结果就只能A第二个点
后来wa掉以后发现如果有环的时候不进行缩点的话，由于两个不相同的半联通子图满足他们至少有一个点不相同，而如果按照我上面的思路的话我们下面的图跑出来会是3个半连通子图，而且最长的链会是3而正确结果是2 1
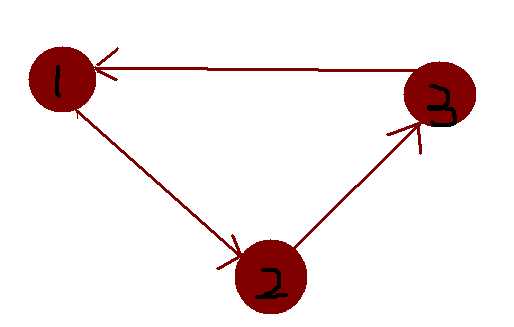这样的话我们就必须缩点了，我们先tarjan求强连通分量，然后在进行缩点，对跑出来的新图进行拓扑排序，然后在拓扑排序里面加dp。
仔细考虑了一下，好像我dfs然后在加暴力枚举根本就不可行、、、 #include<queue> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 1100000 using namespace std; bool vis[N],vist[N]; int n,m,x,y,s,tot,tat,mod,ans1,ans2,top,tim; int in[N],ss[N],dfn[N],low[N],head[N],head1[N],ans[N],sum[N],stack[N],belong[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } struct Edge { int to,from,next; }edge[N],edge1[N]; int add(int x,int y) { tot++; edge[tot].to=y; edge[tot].from=x; edge[tot].next=head[x]; head[x]=tot; } int add1(int x,int y) { tat++; edge1[tat].to=y; edge1[tat].from=x; edge1[tat].next=head1[x]; head1[x]=tat; } int tarjan(int now) { dfn[now]=low[now]=++tim; vis[now]=true; stack[++top]=now; for(int i=head[now];i;i=edge[i].next) { int t=edge[i].to; if(vis[t]) low[now]=min(low[now],dfn[t]); else if(!dfn[t]) tarjan(t),low[now]=min(low[now],low[t]); } if(low[now]==dfn[now]) { s++,belong[now]=s,ss[s]++; for(;stack[top]!=now;top--) belong[stack[top]]=s,vis[stack[top]]=false,ss[s]++; vis[now]=false,top--; } } int shink_point() { for(int i=1;i<=n;i++) for(int j=head[i];j;j=edge[j].next) if(belong[i]!=belong[edge[j].to]) add1(belong[i],belong[edge[j].to]); } int dfs(int x) { vist[x]=true; for(int i=head1[x];i;i=edge1[i].next) { int t=edge1[i].to; if(!vist[t]) dfs(t); in[t]=1; } vist[x]=false; } int tpsort(int s,int * in) { memset(sum,0,sizeof(sum)); queue<int>q; q.push(s);sum[s]=ss[s]; while(!q.empty()) { int x=q.front();q.pop(); for(int i=head1[x];i;i=edge1[i].next) { int t=edge1[i].to; if(in[t]==0) continue; in[t]--; if(in[t]==0) q.push(t); sum[t]=max(sum[t],sum[x]+ss[t]); } } } int main() { n=read(),m=read();mod=read(); for(int i=1;i<=m;i++) x=read(),y=read(),add(x,y); for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); shink_point(); memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { if(vis[belong[i]]) continue; vis[belong[i]]=true; memset(in,0,sizeof(in)); dfs(belong[i]);tpsort(belong[i],in); sort(sum+1,sum+1+n); ans[i]=sum[n]; ans1=max(ans1,ans[i]); } for(int i=1;i<=s;i++) if(ans[i]==ans1) ans2++; printf("%d\\n%d\\n",ans1,ans2); return 0; }
怎么跑？？
我们先考虑一个问题：在tarjan缩完点以后我们在建新图的时候一定会建出重边来，但是我们要进行拓扑排序的话就不可以有重边，所以我们要在进行缩点后建图的时候一定要判断这条边是否是重边，我们用一个map数组来判断。
然后我们在拓扑排序里面跑dp，为什么要用拓扑排序？？因为通拓扑排序可以很容易的找出最长链。
怎么dp？？ 我们在第一部找出它的最大半联通子图的时候，其实找的就是最长链，我们把它最长链里面的权值进行合并就行。我们用一个ans记录到达当前点的最大权值，用v表示当前节点，用x表示与v连通那个点。由于我们有好几条路径可以到达v点，而我们要统计的是最大的半连通子图的大小，所以我们在对当前点更新的时候则为ans[v]=max(ans[v],ans[x])为什么是这样？？因为我们对于每一条链的ans[x]是一直在更新的。这样我们就可以把最大的半联通子图统计出来。ans1=max（ans1,ans[i]）.其次我们还要统计方案数。我们用数组dp记录到当前点的方案数，用数组deep记录到当前点的子图的大小， 然后我们判断这个点的deep值是否等于他父节点的deep值（暂且这样叫吧、、）如果相等的话就说明出现了另一种方案数，那么dp[t]=dp[t]+dp[x]（加法原理其内容是：做一件事情，完成它有N类方式，第一类方式有M1种方法，第二类方式有M2种方法，……，第N类方式有M(N)种方法，那么完成这件事情共有M1+M2+……+M(N)种方法。）如果当前点的deep小与其父节点的deep那么我们对其dp进行修改，dp[t]=dp[x],deep[t]=deep[x]
#include<map> #include<queue> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 110000 using namespace std; bool vis[N],vist[N]; int n,m,x,y,s,tot,tat,mod,ans1,ans2,top,tim; int in[N],dp[N],dfn[N],low[N],deep[N],head[1100000],head1[1100000],ans[N],sum[N],stack[N],belong[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } struct Edge { int to,from,next; }edge[1100000],edge1[1100000]; int add(int x,int y) { tot++; edge[tot].to=y; edge[tot].from=x; edge[tot].next=head[x]; head[x]=tot; } int add1(int x,int y) { tat++; edge1[tat].to=y; edge1[tat].from=x; edge1[tat].next=head1[x]; head1[x]=tat; } int tarjan(int now) { dfn[now]=low[now]=++tim; vis[now]=true; stack[++top]=now; for(int i=head[now];i;i=edge[i].next) { int t=edge[i].to; if(vis[t]) low[now]=min(low[now],dfn[t]); else if(!dfn[t]) tarjan(t),low[now]=min(low[now],low[t]); } if(low[now]==dfn[now]) { s++,belong[now]=s,sum[s]++; for(;stack[top]!=now;top--) belong[stack[top]]=s,vis[stack[top]]=false,sum[s]++; vis[now]=false,top--; } } map<int,int>ma[N]; int shink_point() { for(int i=1;i<=n;i++) for(int j=head[i];j;j=edge[j].next) if(belong[i]!=belong[edge[j].to]) if((++ma[belong[i]][belong[edge[j].to]])==1) { add1(belong[i],belong[edge[j].to]); in[belong[edge[j].to]]++; } } int tpsort() { queue<int>q; for(int i=1;i<=s;i++) if(!in[i]) q.push(i),dp[i]=1; while(!q.empty()) { int x=q.front();q.pop();ans[x]+=sum[x],deep[x]+=sum[x]; for(int i=head1[x];i;i=edge1[i].next) { int t=edge1[i].to; in[t]--; if(!in[t]) q.push(t); ans[t]=max(ans[t],ans[x]); if(deep[t]==deep[x]) dp[t]=(dp[t]+dp[x])%mod; else if(deep[t]<deep[x]) dp[t]=dp[x],deep[t]=deep[x]; } } for(int i=1;i<=n;i++) ans1=max(ans1,ans[i]); for(int i=1;i<=n;i++) if(ans[i]==ans1) ans2=(ans2+dp[i])%mod; } int main() { n=read(),m=read();mod=read(); for(int i=1;i<=m;i++) x=read(),y=read(),add(x,y); for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); shink_point(); tpsort(); printf("%d\\n%d\\n",ans1,ans2); return 0; }
以上是关于tyvj——P3524 最大半连通子图的主要内容，如果未能解决你的问题，请参考以下文章