利用谱聚类算法解决非完全图的聚类
Posted Jachin的博客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了利用谱聚类算法解决非完全图的聚类相关的知识,希望对你有一定的参考价值。
在处理非完全图的聚类时候,很难找到一个有效的聚类算法去做聚类。
对于下图来说,10号点和15号点的位置相隔并不是那么近,如用普通聚类算法对下图做聚类,通常会把10号点和15号点聚在一个类上,所以一般的聚类效果并没有那么好。
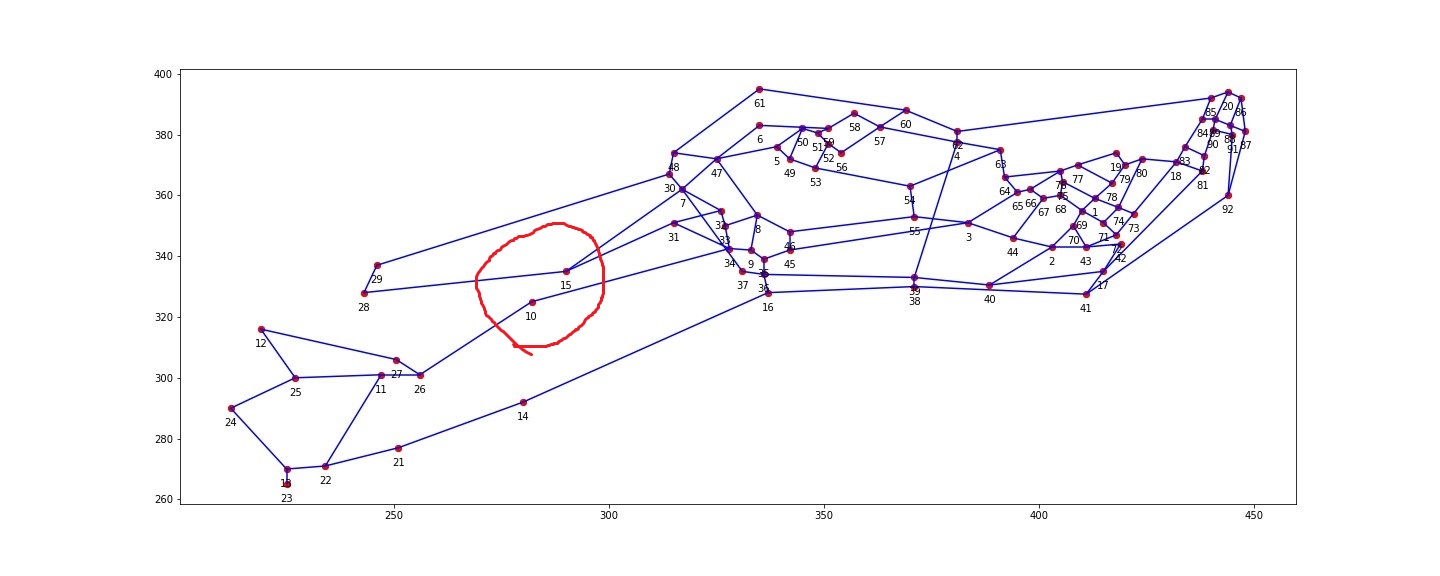
而谱聚类,就很能很好的处理这类问题。
下面我们来重点介绍谱聚类
谱聚类(SpectralClustering),就是要把样本合理地分成两份或者K份。从图论的角度来说,谱聚类的问题就相当于一个图的分割问题。即给定一个图G = (V, E),顶点集V表示各个样本,带权的边表示各个样本之间的相似度,谱聚类的目的便是要找到一种合理的分割图的方法,使得分割后形成若干个子图,连接不同子图的边的权重(相似度)尽可能低,同子图内的边的权重(相似度)尽可能高。物以类聚,人以群分。
(一) 算法步骤
- 根据数据构造一个Graph,Graph的每一个节点对应一个数据点,将各个点连接起来(随后将那些已经被连接起来但并不怎么相似的点,通过cut/RatioCut/NCut 的方式剪开),并 且边的权重用于表示数据之间的相似度。把这个Graph用邻接矩阵的形式表示出来,记为 W。
- 把W的每一列元素加起来得到N个数,把它们放在对角线上(其他地方都是零),组成一个的对角矩阵,记为度矩阵D,并把的结果记为拉普拉斯矩阵。
- 求出L的前k个特征值(前k个指按照特征值的大小从小到大排序得到),以及对应的特征向量。
- 把这k个特征(列)向量排列在一起组成一个的矩阵,将其中每一行看作k维空间中的一个向量,并使用 K-means 算法进行聚类。聚类的结果中每一行所属的类别就是原 来 Graph 中的,因此节点亦即最初的N个数据点分别所属的类别。
(二) 谱聚类的实现
python编程,利用sklearn.cluster 下的 SpectralClustering可以很轻易的实现
from sklearn.cluster import SpectralClustering labels=SpectralClustering(affinity=\'nearest_neighbors\',n_clusters=20, n_neighbors=3).fit_predict(route)
#labels=
[ 3, 3, 5, 7, 8, 8, 9, 4, 4, 15, 15, 2, 2, 15, 16, 17, 18,
13, 1, 12, 2, 2, 2, 2, 2, 15, 15, 16, 16, 9, 4, 4, 4, 4,
17, 17, 17, 14, 14, 14, 18, 18, 3, 5, 4, 4, 9, 9, 8, 8, 8,
8, 8, 5, 5, 8, 19, 19, 8, 19, 8, 7, 7, 6, 6, 6, 6, 11,
3, 3, 3, 3, 3, 3, 11, 11, 11, 1, 1, 1, 13, 13, 13, 10, 12,
12, 0, 0, 10, 10, 0, 0]
其中:
1)n_clusters:代表我们在对谱聚类切图时降维到的维数。如分为20个聚类簇,n_clusters=20。
2) affinity: 也就是我们的相似矩阵的建立方式。可以选择的方式有三类,第一类是 \'nearest_neighbors\',即K邻近法;第二类是\'precomputed\',即自定义相似矩阵;第三类是全连接法,可以使用各种核函数来定义相似矩阵,还可以自定义核函数。基于对有向图的聚类,本文的参数选择是,affinity=\'nearest_neighbors\', n_neighbors=3。
再把图画出来,完美解决类似于10号和15号坐标分成一类的问题。结果如下图
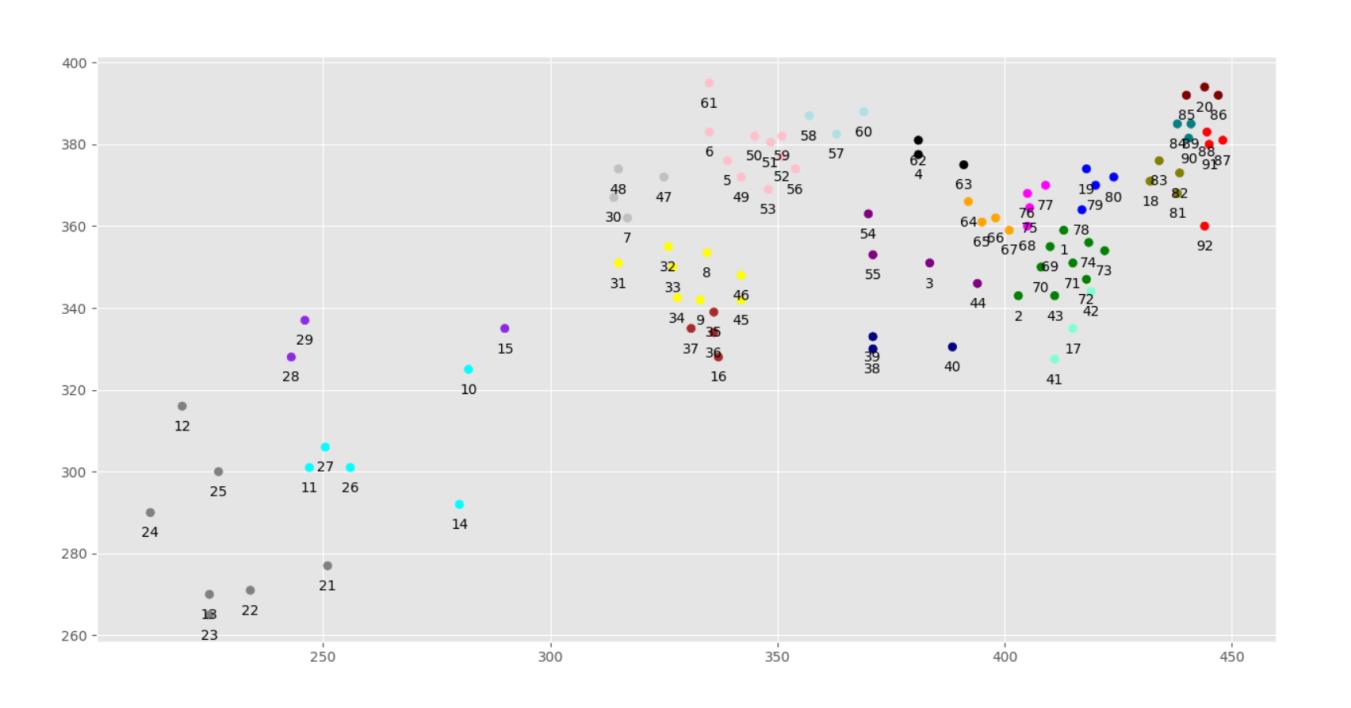
这个例子的实现所需要的数据和代码已经上传到github:https://github.com/yjx7/-SpectralClustering.git 有用给个star谢谢啦
以上是关于利用谱聚类算法解决非完全图的聚类的主要内容,如果未能解决你的问题,请参考以下文章