学习通用函数：快速的元素级数组函数Numpy

Posted 2020-10-05 Aric Zeng

通用函数（即ufunc）是一种对ndarray中的数据执行元素级运算的函数。可以将其看做简单函数（接受一个或多个标量值，并产生一个或多个标量值）的矢量化包装器。

 sqrt 和 exp为一元（unary）ufunc，add或maxinum接受2个数组，因此也叫二元(binary) ufunc, 并返回一个结果数组

import numpy as np
arr = np.arange(10)

np.sqrt(arr)
Out[110]: 
array([ 0.        ,  1.        ,  1.41421356,  1.73205081,  2.        ,
        2.23606798,  2.44948974,  2.64575131,  2.82842712,  3.        ])

np.exp(arr)
Out[111]: 
array([  1.00000000e+00,   2.71828183e+00,   7.38905610e+00,
         2.00855369e+01,   5.45981500e+01,   1.48413159e+02,
         4.03428793e+02,   1.09663316e+03,   2.98095799e+03,
         8.10308393e+03])

x = np.random.randn(8)
y = np.random.randn(8)
x,y
Out[112]: 
(array([-1.68554158, -0.62988644, -0.65300182, -0.9357815 , -0.58973656,
        -1.13627121, -0.25952295, -0.7144267 ]),
 array([ 0.45716238,  0.49681059,  0.61541084, -2.41726508, -0.40145024,
        -0.74636291, -0.31083867,  0.58094538]))

np.maximum(x, y) #元素级最大值
Out[113]: 
array([ 0.45716238,  0.49681059,  0.61541084, -0.9357815 , -0.40145024,
       -0.74636291, -0.25952295,  0.58094538])

但有些ufunc可以返回多个数组，但不常见。例如modf, 它是python内置函数divmod的矢量化版本，用于浮点数组的小数和整数部分。

arr = np.random.randn(7) * 5

arr
Out[116]: 
array([-8.13879901,  0.5628696 ,  0.50146831, -0.94937254, -4.13344095,
        6.55263049,  9.20516911])

np.modf(arr)
Out[117]: 
(array([-0.13879901,  0.5628696 ,  0.50146831, -0.94937254, -0.13344095,
         0.55263049,  0.20516911]), array([-8.,  0.,  0., -0., -4.,  6.,  9.]))

一元ufunc

注意，log1p，为log(1+X),  底数为1+X  ;  

          ceil 为大于等于该值的最小整数；

          floor 即小于等于该值的最大整数

          rint 将各元素值四舍五入到最接近的整数，保留dtype

          modf 将数组的小数和整数部分以两个独立数组的形式返回

          logical_not  计算各元素的not x的真值，相当于-arr

二元ufunc

常用的应该为add 加、subtract减 、multiply 乘、divide除、 power ， maximum(fmax), minimum(fmin), mod

 

 1 、利用数组进行数据处理

numpy 数组可以将许多种数据处理任务表述为简洁的数组表达式（否则需要编写循环）。用数组表达式代替循环的做法，通过被称为矢量化。一般来说，矢量化数组运算要比造价的纯python方式快上一两个数量级（甚至更多），尤其是各种数值计算。

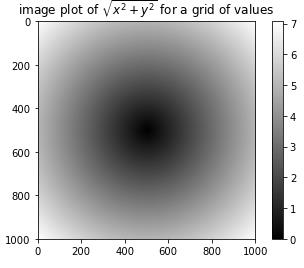
points = np.arange(-5, 5, 0.01) #1000个间隔相等的点

xs, ys = np.meshgrid(points, points)

ys
Out[120]: 
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ..., 
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

对该函数的求值运算，把这两个数组当做两个浮点数那样编写表达式即可：

import matplotlib.pyplot as plt

z = np.sqrt(xs ** 2 + ys ** 2)

z

Out[123]: 
array([[ 7.07106781,  7.06400028,  7.05693985, ...,  7.04988652,
         7.05693985,  7.06400028],
       [ 7.06400028,  7.05692568,  7.04985815, ...,  7.04279774,
         7.04985815,  7.05692568],
       [ 7.05693985,  7.04985815,  7.04278354, ...,  7.03571603,
         7.04278354,  7.04985815],
       ..., 
       [ 7.04988652,  7.04279774,  7.03571603, ...,  7.0286414 ,
         7.03571603,  7.04279774],
       [ 7.05693985,  7.04985815,  7.04278354, ...,  7.03571603,
         7.04278354,  7.04985815],
       [ 7.06400028,  7.05692568,  7.04985815, ...,  7.04279774,
         7.04985815,  7.05692568]])
plt.imshow(z, cmap = plt.cm.gray);
plt.colorbar()
plt.title("image plot of $\\sqrt{x^2 + y^2}$ for a grid of values")
Out[124]: <matplotlib.text.Text at 0xa4987b8>


 

2、将条件逻辑表述为数组运算

 np.where函数的应用

 

xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])

cond = np.array([True, False, True, True, False])

result = np.where(cond, xarr, yarr)

result
Out[8]: array([ 1.1,  2.2,  1.3,  1.4,  2.5])

np.where的第二个和第三个参数不必是数组，它们都可以是标量值

在数据分析的工作中，where 通常用于根据另一个数组而产生一个新的数组

将所有正值替换为2，负值替换为-2，用np.where实现，如下

arr = np.random.randn(4, 4)

np.where(arr>0, 2, -2)
Out[3]: 
array([[ 2, -2,  2,  2],
       [-2, -2,  2,  2],
       [-2,  2,  2,  2],
       [ 2, -2, -2, -2]])

np.where(arr > 0, 2, arr)
Out[4]: 
array([[ 2.        , -0.92801035,  2.        ,  2.        ],
       [-1.57758182, -0.0736849 ,  2.        ,  2.        ],
       [-1.4098105 ,  2.        ,  2.        ,  2.        ],
       [ 2.        , -0.71143105, -0.02427058, -0.05762485]])

3、数学和统计方法

可以通过数组上的一组数学函数对整个数组或某个轴向的数据进行统计计算。

sum、 mean以及标准差std等聚合计算（aggregation , 通常叫约简（reduction））既可以当作数组的实例方法调用，也可以当作顶级numpy函数使用

arr = np.random.randn(5, 4)  #正态分布的数据

arr.mean()
Out[6]: 0.28582428334403248
np.mean(arr)
Out[7]: 0.28582428334403248
arr.sum()
Out[8]: 5.7164856668806499

arr
Out[9]: 
array([[-0.13917863,  0.66047645, -0.17906466, -0.96550224],
       [ 1.49250566,  0.21480886,  1.21176167,  0.81824045],
       [ 0.59244167,  1.83206294, -0.96335555,  0.53373714],
       [ 0.54441794, -1.17739363,  0.73760941, -1.27415443],
       [-0.48136206,  0.66501484, -0.61352379,  2.20694362]])

mean和sum这类的函数可以接受一个axis参数（用于计算该轴向上的统计值），最终结果是一个少一维的数组

arr.mean(axis = 1)
Out[10]: array([-0.15581727,  0.93432916,  0.49872155, -0.29238018,  0.44426815])

arr.sum(0)
Out[11]: array([ 2.00882458,  2.19496946,  0.19342708,  1.31926454])

arr.sum(axis = 1)
Out[12]: array([-0.62326908,  3.73731664,  1.99488621, -1.16952071,  1.77707261])

其他如cumsum和cumprod之类的方法则不聚合，而是产生一个由中间结果组成的数组：

arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 9]])

arr
Out[15]: 
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 9]])
#列加
arr.cumsum(0)
Out[16]: 
array([[ 0,  1,  2],
       [ 3,  5,  7],
       [ 9, 12, 16]], dtype=int32)
#横加
arr.cumsum(1)
Out[17]: 
array([[ 0,  1,  3],
       [ 3,  7, 12],
       [ 6, 13, 22]], dtype=int32)
#列乘
arr.cumprod(0)
Out[18]: 
array([[ 0,  1,  2],
       [ 0,  4, 10],
       [ 0, 28, 90]], dtype=int32)
#横乘
arr.cumprod(1)
Out[19]: 
array([[  0,   0,   0],
       [  3,  12,  60],
       [  6,  42, 378]], dtype=int32)

基本数组统计方法

注意：argmin, argmax最大和最小元素的索引

 4、用于布尔型数组的方法

布尔值会被强制转换为1（True）和0 （False）。因此，sum经常被用来对布尔型数组中的True值计数

arr = np.random.randn(100)

(arr>0).sum() #正值的数量
Out[21]: 45

另外两个方法any 和 all，它们对布尔型数组非常有用，any用于测试数组中是否存在一个或多个True，而all则检查数组中所有值是否都是True

bools = np.array([False, False, True, False])

bools.any()
Out[23]: True

bools.all()
Out[24]: False

这两个方法也能用于非布尔型数组，所有非0元素将会被当做True

 5、排序

Numpy数组也可能通过 sort 方法就地排序

 

arr = np.random.randn(8)

arr
Out[4]: 
array([ 0.33611356, -0.62674777, -1.30911271, -0.36269327,  0.1123545 ,
        0.32001726,  0.18023484,  0.85115163])

arr.sort()

arr
Out[6]: 
array([-1.30911271, -0.62674777, -0.36269327,  0.1123545 ,  0.18023484,
        0.32001726,  0.33611356,  0.85115163])

多维数组可以在任何一个轴向上进行排序，只需将轴编号传给sort即可

arr = randn(5, 3)

顶级方法np.sort返回的是数组的已排序副本，而就地排序则会修改数组本身，计算数组分位数最简单的办法是对其进行排序，然后选取特定位置的值

 

 6、唯一化以及其他的集合逻辑

numpy提供了一些针对一维ndarray的基本集合运算，最常用的可能要数np.unique了，它用于找出数组中的唯一值并返回已排序的结果

names = np.array([\'Bob\', \'Joe\', \'Will\', \'Bob\', \'Will\', \'Joe\', \'Joe\'])

np.unique(names)
Out[11]: 
array([\'Bob\', \'Joe\', \'Will\'], 
      dtype=\'<U4\')

ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])

np.unique(ints)
Out[13]: array([1, 2, 3, 4])

另一个函数np.in1d用于测试一个数组中的值在另一个数组中的成员资格，返回一个布尔型数组

values = np.array([6, 0, 0, 3, 2, 5, 6])

np.in1d(values, [2, 3, 6])
Out[16]: array([ True, False, False,  True,  True, False,  True], dtype=bool)

集合函数如下：

注意： intersect1d(x, y) 计算x和y的交集；union1d(x, y)计算x和y的并集；in1d(x, y),  setdiff1d(x, y), setxor1d(x, y)

 7、将数组以二进制格式保存到磁盘

np.load和np.save是读写磁盘数组数据的两个主要函数。默认情况一上，数组是以未压缩的原始二进制格式保存在扩展名为.npy的文件中的。

 8、线性代数

numpy 提供一个用于矩阵乘法的dot函数

9、常用的numpy.linalg函数

10、随机数的生成

numpy.random模块对python内置的random进行了补充

normal得到一个标准正态布样本数组