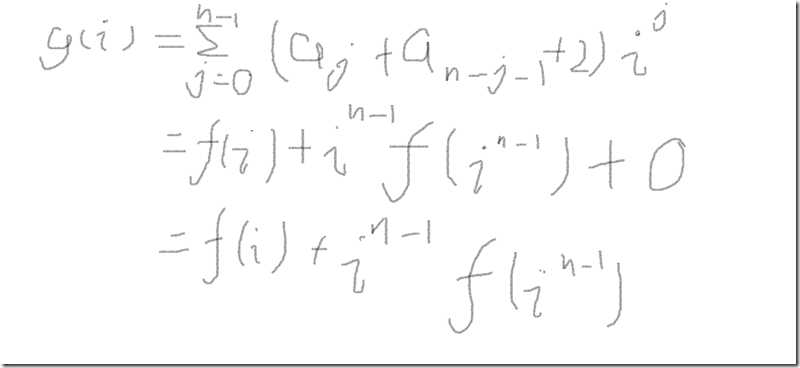XJOI 郎思轲模拟题
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了XJOI 郎思轲模拟题相关的知识,希望对你有一定的参考价值。
今天比赛的是郎思轲出的模拟题,比较偏数学.
全国青少年奥林匹克联赛
CCF-NOIP 2017模拟试题
提高组(复赛)day1
竞赛时间:210分钟
命题:郎思轲
题目一览:
| 题目名称 | 不定长数组 | 台球游戏 | 对称的多项式 |
| 题目类型 | 传统型 | 传统型 | 传统型 |
| 目录 | vector | billiards | poly |
| 可执行文件名 | vector | billiards | poly |
| 输入文件名 | vector.in | billiards.in | poly.in |
| 输出文件名 | vector.out | billiards.out | poly.out |
| 每个测试点时限 | 1.0秒 | 2.0秒 | 2.0秒 |
| 内存限制 | 512MB | 512MB | 512MB |
| 测试点数目 | 20 | 20 | 20 |
| 每个测试点分值 | 5 | 5 | 5 |
提交源程序文件名:
| 对于C++ 语言 | vector.cpp | billiards.cpp | poly.cpp |
| 对于C 语言 | vector.c | billiards.c | poly.c |
| 对于Pascal语言 | vector.pas | billiards.pas | poly.pas |
编译选项:
| 对于C++ 语言 | -O2 -lm | -O2 -lm | -O2 -lm |
| 对于C 语言 | -O2 -lm | -O2 -lm | -O2 -lm |
| 对于Pascal语言 | -O2 | -O2 | -O2 |
注意事项:
1.文件名(程序名和输入输出文件名)必须使用英文小写。
2.除非特殊说明,结果比较方式均为忽略行末空格及文末回车的全文比较。
3.C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
1. 不定长数组
vector
【问题描述】
Description
小A是一个C++初学者,最近他学会了不定长数组vector的使用方法,于是他很兴奋,就把他的好多文件存到了好多vector中。
最终小A得到了n个vector,每个vector都不是空的,每个vector的类型都为字符类型char,一个vector代表小A的一个文件;由于小A只喜欢简洁的英文小写字母,因此他的文件中仅包含英文小写字母。
接下来小A发现他每次只能对一个vector v[i] 进行这一些操作:
l v[i].push_back(ch) 在vector v[i]后添加一个字符ch
l v[i].pop_back() 在vector v[i]后删除一个字符
l v[i][j]=ch 将vector v[i]的第j+1个字符修改为ch
现在小A觉得这么多不同的文件看起来太杂乱了,因此他想对一些文件进行修改,从而使得所有的文件都相同;他想知道他最少要做几次操作能使所有的vector均相同(可以把vector修改为空,vector的长度也没有上限),请你帮他计算这个结果。
在修改文件之前,小A还想知道把任意两个vector修改为相同需要的操作数(每一次操作你可以任选一个vector进行)。设为vector[i]与vector[j]修改为相同需要的操作数,你只需要回答
的值。
注:如果你对C++或者不定长数组不熟悉,你只需对题意有大致理解即可,这并不会影响解题。
【输入格式】
Input
从文件vector.in中读取数据;
输入文件第一行一个正整数n,表示vector的个数;
接下来n行,第i行一个仅包含英文小写字母的字符串,第j个字符表示vector[i]的第j个字符;
最后一行为两个0或1的数k1,k2,含义见输出格式。
由于输入文件可能比较大,建议C++选手不要使用过慢的读入方式。
【输出格式】
Output
输出到文件vector.out中;
输出共k1+k2行;
若k1=1,输出一行,为上文所述的 的值;
接下来,若k2=1,输出一行,即为使所有的vector均相同的最少操作次数。
【输入样例1】
Sample Input #1
3
he
she
him
1 1
【输出样例1】
Sample Output #1
8
5
【输入输出样例1说明】
在这个样例中,你两个询问都需要回答。
对于第一个询问,可以知道=2,操作方案为:
step1:v[1][1]=‘i’,操作后vector[1]表示的串为“hi”
step2:v[i].pop_back(),操作后vector[2]表示的串也为“hi”
可以知道2步是最少的方案。
以此类推可计算出=3,=3,因此答案为2+3+3=8;
对于第二个询问,可以把所有的字符串均改为“hi”;
此时答案为1+3+1=5,可以知道5为最优解。
【输入样例2】
Sample Input #2
10
also
rate
rateg
d
edee
edge
lae
reai
aslie
ead
0 1
【输出样例2】
Sample Output #2
29
【输入输出样例3、输入输出样例4】
见选手文件下的vector3.in/vector3.ans、vector4.in/vector4.ans
其中vector3.in数据范围同第3个测试点,vector4.in数据范围同第16个测试点。
【数据范围与约定】
l 对于100%的数据,n≥2,不存在空字符串。
| 测试点编号 | n | len | maxlen | k1 | k2 |
| 1 | ≤10 | ≤10 | ≤5 |
1 |
1 |
| 2 | |||||
| 3 | =100 | =500 | =5 | ||
| 4 | |||||
| 5 | =300 | =30000 | =100 |
1 |
0 |
| 6 | ≤1000 | ||||
| 7 | ≤5000 | ≤10000 | ≤100 | ||
| 8 | ≤10000 | ||||
| 9 | ≤100000 | ≤1000000 | ≤1000000 | ||
| 10 | |||||
| 11 | =300 | =30000 | =100 |
0 |
1 |
| 12 | ≤1000 | ≤1000 | ≤1000 | ||
| 13 | |||||
| 14 | ≤100000 | ≤1000000 | ≤1000000 | ||
| 15 | |||||
| 16 |
≤100000 |
≤1000000 |
≤1000000 |
1 |
1 |
| 17 | |||||
| 18 | |||||
| 19 | |||||
| 20 |
注:表示所有vector的元素个数之和,maxlen表示所有vector中最大的元素个数。
2. 台球游戏
billiards
【问题描述】
Description
最近小B迷上了台球游戏,这个游戏在一张矩形球桌上进行,基本规则是将球打进球桌边缘上的球洞就会得分;为了让题目更有趣,在本题中我们认为球桌大小、球洞位置和球洞个数是不确定的,但保证球桌的四角均有球洞,在球桌长边上的两个相邻球洞距离都相等,短边上的两个相邻球洞距离也都相等。
我们记球桌长边为n,短边为m,长边上的两个相邻球洞距离为,长边上的两个相邻球洞距离为,下图表示了n=8,m=6,=4,=2时的球桌的形态 (黑点表示球洞):
为了表示方便,我们把所有球洞进行标号:先将矩形下边界的球洞从左上角至右上角分别标号为到,然后同样将下边界的球洞标为到;最后若,将左边界、右边界除角上的球洞从上到下依次标号为到,到,你可以参照上图来帮助理解标号方式。
现在,球桌左上角有一只台球(注意:虽然球桌左上角一定有球洞,但开始时球并不会进入这个洞),这只台球会沿一定角度射出,碰到边缘会反弹(反弹时入射角等于反射角),你可以认为台球的轨迹不会弯曲,但台球碰到边缘k次(开始时在左上角不算在内)后会立即停下,小B想知道,对于给定的n,m, , ,k和刚开始射出的角度,台球最终会进入哪个洞。
【输入格式】
Input
从文件billiards.in中读取数据;
第一行一个整数T表示数据组数;
接下来T行,每行7个正整数n,m, , ,a,b,k,其中n,m, , ,k的含义为题目描述所述,a,b表示台球初始射出的轨迹同的夹角,记该夹角为,则。
【输出格式】
Output
输出到文件billiards.out中;
输出T行,对于每个数据输出台球最终掉进的球洞编号以及球碰到边缘次数(开始时在左上角不算在内);若直到台球停下球还没有进洞,则输出-1。
【输入样例1】
Sample Input #1
3
8 6 4 2 1 1 2
8 6 4 2 1 1 1
9 5 3 5 1 1 20
【输出样例1】
Sample Output #1
D1 1
-1
B1 3
【输入输出样例1说明】
对于第一、二个数据,球桌形态及台球轨迹如下左图
根据上左图可以看出,第一个数据台球反弹1次进入了球洞,而第二个数据台球撞击一次后停了下来而没有进洞;
根据上右图可以看出,第三个数据台球反弹3次后进了球洞。
【输入输出样例2、输入输出样例3】
见选手文件下的billiards2.in/billiards2.ans、billiards3.in/billiards3.ans
其中billiards2.in数据范围同第6个测试点,billiards3.in数据范围同第16个测试点。
【数据范围与约定】
l 对于100%的数据,,,m≤n, 保证a,b互质。
| 测试点编号 | n,m | a,b | k | T | p |
| 1 |
≤10 |
=1 | =1 |
≤10 |
1 |
| 2 | ≤2 | ||||
| 3 | ≤10 | ||||
| 4 | ≤100 | ≤100 | |||
| 5 | ≤1000 | ≤1000 |
≤1000 | ||
| 6 | ≤10000 | ≤10000 |
≤50 |
0 | |
| 7 |
≤ | ≤ | |||
| 8 |
≤100000 | ||||
| 9 | |||||
| 10 |
=1 | ||||
| 11 |
≤ |
1 | |||
| 12 | |||||
| 13 |
≤ | ||||
| 14 | |||||
| 15 | |||||
| 16 |
≤100000 |
0 | |||
| 17 | |||||
| 18 | |||||
| 19 | |||||
| 20 |
注:当时,p=1,否则p=0。
3. 对称的多项式
poly
【问题描述】
Description
小C现在有一个数n和一个系数均在模n+1意义下的次数界为n
的多项式,但小C并不喜欢这个多项式,因为这个多项式
并不是对称的,而小C希望对这个多项式进行变形,成为另一个系数均在模p意义下的对称的多项式;
小C的变形方式如下:
变形得到的多项式 ,如n=4,原多项式f(x)=3+2+x+4,则g(x)=((3+4+2) mod 5)+((2+1+2) mod 5)+((2+1+2) mod 5)x+((3+4+2) mod 5)=4+4。
现在小C给了你原多项式f(x),请你帮他转成对称的多项式g(x)。
小C还发现了一个性质:给出多项式,能求出x取1到n时的多项式在模n+1意义下的值,而给出这些值也能唯一确定一个系数在模域下的次数界为n的多项式,因此他决定给你原多项式x取1到n时n个值,而你只要告诉他答案多项式分别在x取1到n时模n+1意义下的值就可以了。
【输入格式】
Input
从文件poly.in中读取数据;
第一行一个正整数n,,题目描述中已经解释过n的含义;
接下来n个整数,第i个整数表示当x取i时原多项式f(x)在模n+1意义下的值f(i)。
【输出格式】
Output
输出到文件poly.out中;
输出一行,n个整数,第i个整数表示当x取i时答案多项式g(x)在模n+1意义下的值g(i),注意0≤g(i)≤n。
【输入样例1】
Sample Input #1
4
0 3 1 2
【输出样例1】
Sample Output #1
3 1 2 0
【输入输出样例1说明】
该样例对应于题目描述中举的例子。
【输入样例2】
Sample Input #2
6
1 2 1 2 1 2
【输出样例2】
Sample Output #2
0 3 6 6 4 0
【输入输出样例3、输入输出样例4】
见选手文件下的poly3.in/poly3.ans、poly4.in/poly4.ans
其中poly3.in数据范围同第4个测试点,poly4.in数据范围同第11个测试点。
【数据范围与约定】
l 对于100%的数据,0≤ f(i)≤ n。
| 测试点编号 | n | 测试点编号 | n |
| 1 | =6 | 11 | =4000 |
| 2 | =16 | 12 | |
| 3 | =22 | 13 |
=49998 |
| 4 | =100 | 14 | |
| 5 | =232 | 15 | |
| 6 | =250 | 16 | |
| 7 | =996 | 17 | |
| 8 |
=2332 | 18 | =100002 |
| 9 | 19 | =500008 | |
| 10 | 20 |
比赛时只做了前两题
第一题是一个暴力统计,没什么好讲
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=100010,LEN=1000100; vector<char>s[N]; char b[LEN]; int n,maxlen,ch[LEN][26],len[N],k1,k2,tot[LEN],righ[LEN],rig[LEN]; ll calc1(){ ll res=0; for (int i=1; i<=n; i++){ for (int j=0; j<len[i]; j++) res+=n-ch[j][s[i][j]-‘a‘]; res+=tot[len[i]]; } return res>>1; } ll calc2(){ ll res=tot[0],re=0; for (int i=0; i<maxlen; i++){ re+=n-ch[i][righ[i]]; res=min(res,re+tot[i+1]); } return res; } int main(){ //freopen("vector3.in","r",stdin); //freopen("A.out","w",stdout); scanf("%d",&n); for (int i=1; i<=n; i++){ scanf("%s",b); for (len[i]=0; b[len[i]]; len[i]++){ s[i].push_back(b[len[i]]); if (++ch[len[i]][b[len[i]]-‘a‘]>rig[len[i]]){ rig[len[i]]=ch[len[i]][b[len[i]]-‘a‘]; righ[len[i]]=b[len[i]]-‘a‘; } tot[len[i]]++; } maxlen=max(maxlen,len[i]); } for (int i=maxlen-2; i>=0; i--) tot[i]+=tot[i+1]; scanf("%d%d",&k1,&k2); if (k1) printf("%lld\\n",calc1()); if (k2) printf("%lld\\n",calc2()); return 0; }
第二题需要每弹一次把地图展开,因为会爆longlong所以用__int128水过
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll INF=1e18; ll n,m,n0,m0,a,b,k,zq1,zq2,ind1,ind2; char ch1,ch2; int t; long double p=1; void solvep0(){ ll A=a*m,B=n0*b,ceng=B/__gcd(A,B),len=(ll)p*A*ceng/b; zq1=(len%n==0?len/n-1:len/n),ind1=len%n/n0; if (ind1==0&&zq1%2==0) ind1=n/n0; if (ind1&&(zq1&1)) ind1=n/n0-ind1; zq1+=ceng-1; ch1=ceng&1?‘B‘:‘A‘; } void solvep1(){ ll A=b*n,B=m0*a,ceng=B/__gcd(A,B),len=(ll)p*A*ceng/a; zq2=(len%m==0?len/m-1:len/m),ind2=len%m/m0; if (ind2==0&&zq2%2==0) ind2=m/m0; if (ind2&&(zq2&1)) ind2=m/m0-ind2; zq2+=ceng-1; ch2=ceng&1?‘D‘:‘C‘; } int main(){ //freopen("billiards3.in","r",stdin); //freopen("B.out","w",stdout); scanf("%d",&t); while (t--){ scanf("%lld%lld%lld%lld%lld%lld%lld",&n,&m,&n0,&m0,&a,&b,&k); if (m0==m){ solvep0(); if (zq1<k) printf("%c%lld %lld\\n",ch1,ind1,zq1); else puts("-1"); }else{ solvep0(); solvep1(); if (zq1<=zq2&&zq1<k) printf("%c%lld %lld\\n",ch1,ind1,zq1); else if (zq2<zq1&&zq2<k) printf("%c%lld %lld\\n",ch2,ind2-1,zq2); else puts("-1"); } } }
第三题是一个奇妙的变换
#include<bits/stdc++.h> using namespace std; const int N=500009; int n,f[N],p; inline int pow(int x,int y){ int res=1; while (y){ if (y&1) res=1ll*res*x%(n+1); x=1ll*x*x%(n+1); y>>=1; } return res; } int main(){ scanf("%d",&n); for (int i=1; i<=n; i++) scanf("%d",&f[i]); printf("%d ",(f[1]+f[1]+2*n)%(n+1)); for (int i=2; i<=n; i++){ p=pow(i,n-1); printf("%d ",(f[i]+1ll*p*f[p]%(n+1))%(n+1)); } }
以上是关于XJOI 郎思轲模拟题的主要内容,如果未能解决你的问题,请参考以下文章