层层递进——宽度优先搜索（BFS）

Posted 2020-10-05 ~不会飞的章鱼~

 问题引入

我们接着上次“解救小哈”的问题继续探索，不过这次是用宽度优先搜索（BFS）。

注：问题来源可以点击这里 http://www.cnblogs.com/OctoptusLian/p/7429645.html

 

最开始小哼在入口（1,1）处，一步之内可以到达的点有（1,2）和（2,1）。

 

但是小哈并不在这两个点上，那小哼只能通过（1,2）和（2,1）这两点继续往下走。

比如现在小哼走到了（1,2）这个点，之后他又能够到达哪些新的点呢？有（2,2）。再看看通过（2,1）又可以到达哪些点呢？可以到达（2,2）和（3,1）。

此时你会发现（2,2）这个点既可以从（1,2）到达，也可以从（2,1）到达，并且都只使用了两步。

注：为了防止一个点多次被走到，这里需要一个数组来记录一个点是否已经被走到过。

 

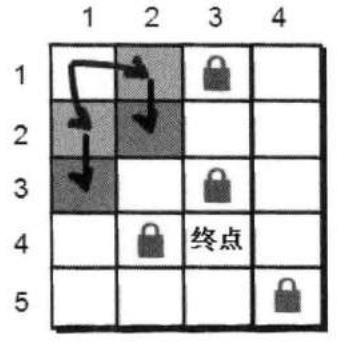
此时小哼2步可以走到的点就全部走到了，有（2,2）和（3,1），可是小哈并不在这两个点上。看来没有别的办法，还得继续往下尝试，看看通过（2,2）和（3,1）这两个点还能到达哪些新的没有走到过的点。

通过（2,2）这个点我们可以到达（2,3）和（3,2），通过（3,1）可以到达（3,2）和（4,1）。

现在三步可以到达的点有（2,3）、（3,2）和（4,1），依旧没有到达小哈的所在点，所以我们需要继续重复刚才的做法，直到找到小哈所在点为止。

 

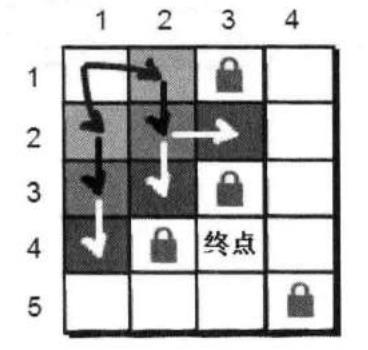
解决步骤

回顾一下刚才的算法，可以用一个队列来模拟这个过程。在这里我们用一个结构体来实现队列

struct note{
    int x;  //横坐标
    int y;  //纵坐标
    int s;  //步数 
};
struct note que[2501];  //因为地图大小不超过50*50，因此队列扩展不会超过2500个
int head,tail;
int a[51][51] = {0};  //用来存储地图 
int book[51][51] = {0};  //数组book的作用是记录哪些点已经在队列中了，防止一个点被重复扩展，并全部初始化为0

/*最开始的时候需要进行队列初始化，即将队列设置为空*/
head = 1;
tail = 1;
//第一步将（1,1）加入队列，并标记（1,1）已经走过。
que[tail].x = 1;
que[tail].y = 1;
que[tail].s = 0;
tail++;
book[1][1] = 1;

 

 

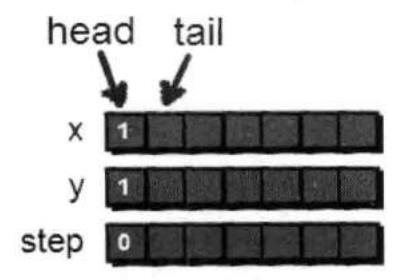
然后从（1,1）开始，先尝试往右走到达了（1,2）。

tx = que[head].x;
ty = que[head].y+1;

 

 

需要判断（1,2）是否越界。

if(tx < 1 || tx > n || ty < 1 || ty > m)
    continue;

 

 

再判断（1,2）是否为障碍物或者已经在路径中。

if(a[tx][ty] == 0 && book[tx][ty] == 0)
{
}

 

 

如果满足上面的条件，则将（1,2）入队，并标记该点已经走过。

book[tx][ty] = 1;  //注意bfs每个点通常情况下只入队一次，和深搜不同，不需要将book数组还原
//插入新的点到队列中
que[tail].x = tx;
que[tail].y = ty;
que[tail].s = que[head].s+1;  //步数是父亲的步数+1
tail++; 

 

 

 

接下来还要继续尝试往其他方向走。

在这里我们规定一个顺序，即按照顺时针的方向来尝试（右→下→左→上）。

我们发现从（1,1）还是可以到达（2,1），因此也需要将（2,1）也加入队列，代码实现与刚才对（1,2）的操作是一样的。

 

对（1,1）扩展完毕后，此时我们将（1,1）出队（因为扩展完毕，已经没用了）。

head++;

 

 

接下来我们需要在刚才新扩展出的（1,2）和（2,1）这两个点上继续向下探索（因为还没有到达小哈所在的位置，所以还需要继续）。

（1,1）出队之后，现在队列的head正好指向了（1,2）这个点，现在我们需要通过这个点继续扩展，通过（1,2）可以到达（2,2），并将（2,2）也加入队列。

 

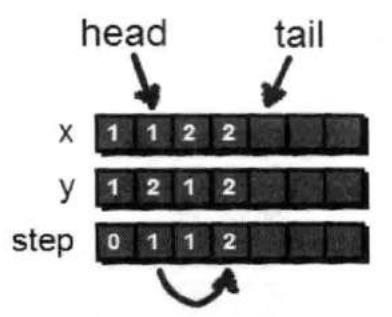
（1,2）这个点已经处理完毕，于是可以将（1,2）出队。（1,2）出队之后，head指向了（2,1）这个点。通过（2,1）可以到达（2,2）和（3,1），但是因为（2,2）已经在队列中，因此我们只需要将（3,1）入队。

 

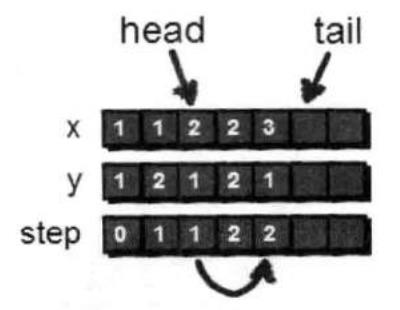
到目前为止我们已经扩展出从起点出发2步以内可以到达的所有点，可是依旧没有到达小哈所在的位置，因此还需要继续扩展，直到找到小哈所在的点才算结束。

为了方便向四个方向扩展，这里需要一个next数组：

int next[4][2] = {  //顺时针方向 
    {0,1};  //向右走 
    {1,0};  //向下走 
    {0,-1};  //向左走 
    {-1,0};  //向上走 
}

 

 

完整代码如下

#include<stdio.h>
struct note{
    int x;  //横坐标
    int y;  //纵坐标
    int f;  //父亲在队列中的编号（本题不需要输出路径，可以不需要f） 
    int s;  //步数 
};
int main()
{
    struct note que[2501];  //因为地图大小不超过50*50，因此队列扩展不会超过2500个
    
    int a[51][51] = {0};  //用来存储地图 
    int book[51][51] = {0};  //数组book的作用是记录哪些点已经在队列中了，防止一个点被重复扩展，并全部初始化为0
    //定义一个用于表示走的方向的数组
    int next[4][2] = {  //顺时针方向 
    {0,1}, //向右走 
    {1,0},  //向下走 
    {0,-1},  //向左走 
    {-1,0},  //向上走 
    };

    int head,tail;
    int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;
    
    scanf("%d %d",&n,&m);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    scanf("%d %d %d %d",&startx,&starty,&p,&q);
    
    //队列初始化
    head = 1;
    tail = 1;
    //往队列插入迷宫入口坐标 
    que[tail].x = startx;
    que[tail].y = starty;
    que[tail].f = 0;
    que[tail].s = 0;
    tail++;
    book[startx][starty] = 1;
    
    flag = 0;  //用来标记是否到达目标点，0表示暂时没有到达， 1表示已到达
    while(head < tail){  //当队列不为空时循环 
        for(k=0;k<=3;k++)  //枚举四个方向 
        {
            //计算下一个点的坐标 
            tx = que[head].x + next[k][0];
            ty = que[head].y + next[k][1];
            if(tx < 1 || tx > n || ty < 1 || ty > m)  //判断是否越界 
                continue;
            if(a[tx][ty] == 0 && book[tx][ty] == 0)  //判断是否是障碍物或者已经在路径中 
                {
                    book[tx][ty] = 1;  //把这个点标记为已经走过。注意bfs每个点通常情况下只入队一次，和深搜不同，不需要将book数组还原
                    //插入新的点到队列中
                    que[tail].x = tx;
                    que[tail].y = ty;
                    que[tail].f = head;  //因为这个点是从head扩展出来的，所以它的父亲是head，本题不需要求路径，因此可省略 
                    que[tail].s = que[head].s+1;  //步数是父亲的步数+1
                    tail++; 
                    
                }
            if(tx == p && ty == q)  //如果到目标点了，停止扩展，任务结束，退出循环 
            {
                flag = 1;  //重要！两句不要写反 
                break;
            }
        }
        if(flag == 1)
            break;
        head++;  //当一个点扩展结束后，才能对后面的点再进行扩展 
    }    
    printf("%d",que[tail-1].s);  //打印队列中末尾最后一个点，也就是目标点的步数 
     //注意tail是指向队列队尾（最后一位）的下一个位置，所以这里需要减1 
    getchar();getchar();
    return 0;         
}

 

 

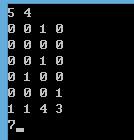
第一行有两个数n m，n表示迷宫的行数，m表示迷宫的列数。

接下来n行m列为迷宫，0表示空地，1表示障碍物。

最后一行四个数，前两个数表示迷宫入口的x和y坐标，后两个为小哈的x和y坐标。

 

写在最后

通过本次学习，我们知道一道问题的解决方法是多种多样的，不光可以用深度优先搜索来解，也可以用宽度优先搜索。

个人感觉宽度优先搜索就像是一次病原体的扩散，目的是要以最短的速度扩散到最广的范围。

注：文章内容源自《啊哈算法》