算法 快速排序

Posted 2020-10-05 细雨蓝枫

快速排序 quick sort

介绍：
　　快速排序（Quicksort）是对冒泡排序的一种改进。在*均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n²)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

原理：

　　通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行，以此达到整个数据变成有序序列，最终完成整个数据排序的目的。 值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

步骤：
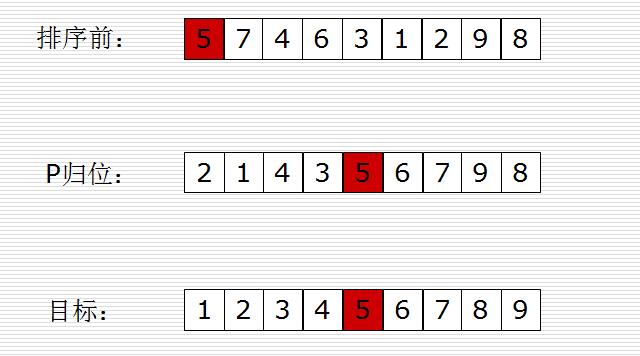
　　1、从数列中挑出一个元素，称为 “基准”（pivot），
　　2、重新排序数列，将基准归位！所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
　　3、递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

　　注：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。要注意的是，排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。 

革新点：先从后扫描(比基准值)小的，再从前扫描(比基准值)大的！

快速排序动画演示：

算法实现：

import random as rd
import time
import sys

sys.setrecursionlimit(100000)

def cal_time(func):
    """
	装饰器打印执行时间
	"""
	def wrapper(*args, **kwargs):
        t1 = time.time()
        x = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time %s secs." % (func.__name__, t2 - t1))
        return x
		
    return wrapper

def partition(data, left, right):
    """
	区内数据排序处理
	快速排序的核心代码。
	其实就是将选取的tmp不断交换，将比它小的换到左边，将比它大的换到右边。
	它自己也在交换中不断变换自己的位置，直到完成所有的交换为止。
	但在函数调用的过程中，pivot_key的值始终不变。
	:param low:左边界索引
	:param high:右边界索引
	:return:分完左右区后tmp所在位置的索引
	"""
	tmp = data[left]
    while left < right:
        while left < right and data[right]>=tmp:
            right-=1
        data[left]=data[right]
        while left < right and data[left]<=tmp:
            left+=1
        data[right]=data[left]
    data[left]=tmp
    return left
	
def _quick_sort(data, left, right):
	"""
	递归调用
	"""
    if left < right:
        mid = partition(data, left, right)
        _quick_sort(data, left, mid - 1)
        _quick_sort(data, mid + 1, right)

@cal_time
def quick_sort(data):
	"""
	调用入口
	"""
    return _quick_sort(data, 0, len(data)-1)
	
li = list(range(100000))
rd.shuffle(li)
quick_sort(li)	

　　

总结：

• 快速排序的时间性能取决于递归的深度。
• 当tmp恰好处于记录关键码的中间值时，大小两区的划分比较均衡，接*一个*衡二叉树，此时的时间复杂度为O(nlog(n))。
• 当原记录集合是一个正序或逆序的情况下，分区的结果就是一棵斜树，其深度为n-1，每一次执行大小分区，都要使用n-i次比较，其最终时间复杂度为O(n^2)。
• 在一般情况下，通过数学归纳法可证明，快速排序的时间复杂度为O(nlog(n))。
• 但是由于关键字的比较和交换是跳跃式的，因此，快速排序是一种不稳定排序。
• 同时由于采用的递归技术，该算法需要一定的辅助空间，其空间复杂度为O(logn)。