Treap

Posted 2020-10-05 lh

先推荐一篇文章和黄学长的代码http://hzwer.com/1712.html    https://wenku.baidu.com/view/c8c11e1e650e52ea55189887.html

Treap，顾名思义，Tree+Heap，它既满足二叉搜索树的性质，又满足堆的性质

对于二叉搜索树，如果我们把数有序加入，那么它的时间效率会退化成O(n)。

我们引入一个随机数（即下文描述的修正值），使得随机数满足堆的性质（小根堆或大根堆，不一定要是完全二叉树），这样就能有效避免退化的情况

Treap可以定义为有以下性质的二叉树：

1.若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值，而且它的根节点的修正值小于等于左子树根节点的修正值；

2.若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值，而且它的根节点的修正值小于等于右子树根节点的修正值；

3.它的左、右子树也分别为Treap。

如何构建treap？

一：旋转

为了维护它的堆性质和二叉搜索树性质，我们引入了一个旋转的概念

左旋：把旋转节点原先父亲的位置用旋转节点代替。把它原先父亲自身和左子树作为它的左子树。把它的左子树作为它原先父亲的右子树

右旋：把旋转节点原先父亲的位置用旋转节点代替。把它原先父亲自身和右子树作为它的右子树。把它的右子树作为它原先父亲的左子树

                                            

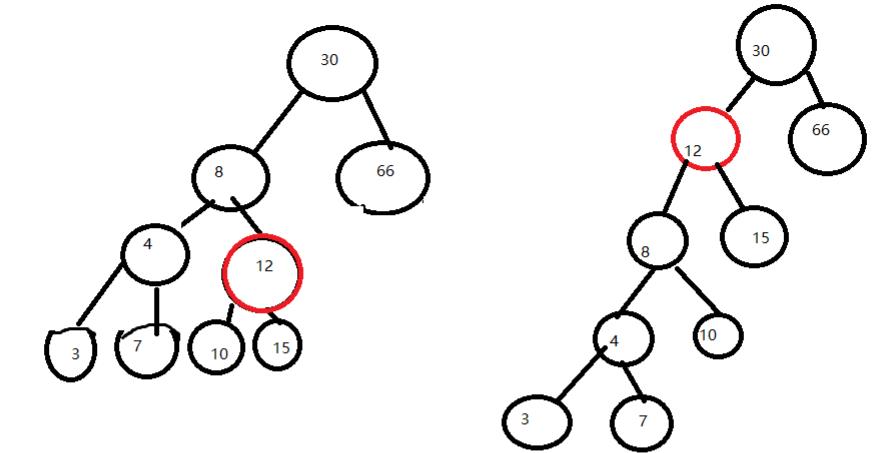
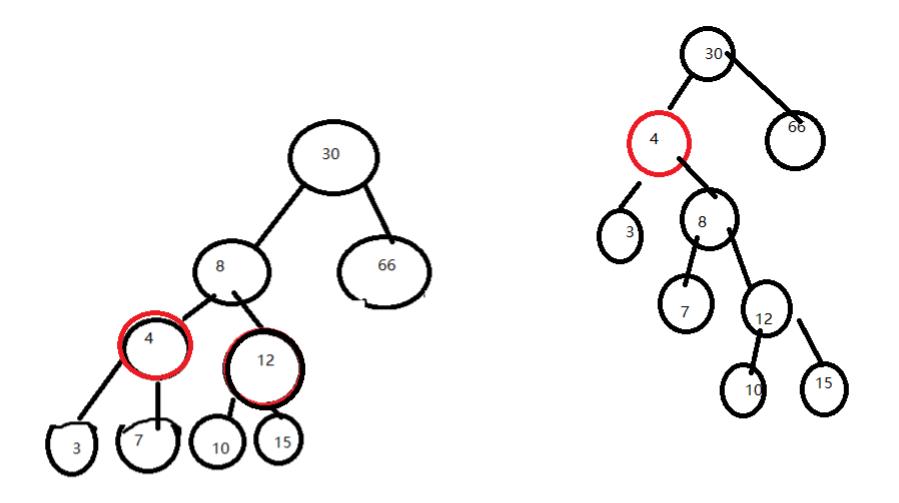
 （左侧图是左旋，右侧图是右旋）

旋转的意义在于：旋转可以使不满足堆序的两个节点通过调整位置，重新满足堆序，而不改变BST性质。

我感觉旋转最麻烦的地方是怎么找到上图中红圈点的父亲的编号(因为没记每个点的父亲，记录的话旋转很麻烦）

通过回溯时传回一个变量来更新它的左（右）孩子（即传回红圈点）

二.查找，遍历方式见二叉搜索树

三.插入

1.从根节点开始插入；

2.如果要插入的值小于当前节点的值，在当前节点的左子树中插入，插入后如果左子节点的修正值小于当前节点的修正值，对当前节点进行右旋；

2.如果要插入的值等于当前节点的值，把当前节点的出现次数+1  （开一个变量记录出现次数）；

3.如果要插入的值大于当前节点的值，在当前节点的右子树中插入，插入后如果右子节点的修正值小于当前节点的修正值，对当前节点进行左旋；

4.如果当前节点为空节点，在此建立新的节点，该节点的值为要插入的值，左右子树为空，插入成功。

旋转可以在建好新节点，回溯的时候进行（具体参见代码）

四.删除

情况一，该节点为叶节点或链节点，则该节点是可以直接删除的节点。若该节点有非空子节点，用非空子节点代替该节点的，否则用空节点代替该节点，然后删除该节点。  

情况二 ，该节点有两个非空子节点。我们的策略是通过旋转，使该节点变为可以直接删除的 节点。如果该节点的左子节点的修正值小于右子节点的修正值，右旋该节点，

使该节点降为右子树的根节点，然后访问右子树的根节点，继续讨论；反之，左旋该节点，使该节点降为左子树的根节点，然后访问左子树的根节点，继续讨论，直到变成可以直接删除的节点。

这样，Treap的基本操作就讲完了。

Treap功能：

一：查最值

查找一个子树的最小值，从子树的根开始访问，如果当前节点左子节点非空，访问当前节点的左子节点；如果当前节点左子节点已经为空，那么当前节点的值就是这个子树的最小值。查最大值同理

二：求前驱后继

每个地方关于前驱后继的定义可能会有所不同（其实就有没有取等）

求一个元素在平衡树(或子树）中的前驱，定义为查找该元素在平衡树中不大于该元素的最大元素。

相似的，求一个元素在平衡树(或子树)中的后继，定义为查找该元素在平衡树中不小于该元素的最小元素。

求前驱： 

1.从根节点开始访问，初始化最优节点为空节点；

2.如果当前节点的值不大于要求前驱的元素的值，更新最优节点为当前节点，访问当前节点的右子节点；

3.如果当前节点的值大于要求前驱的元素的值，访问当前节点的左子节点；

4.如果当前节点是空节点，查找结束，最优节点就是要求的前驱。

求后继同理

三：查询第k大的元素（第k小同理）

如果我们想查找第k小的元素或者询问某个元素在Treap中从小到大的排名时，我们就必须知道每个子树中节点的个数。我们称以一个子树的所有节点的权值之和，为子树的大小。由于插入、删除、旋转等操作，会使每个子树的大小改变，所以我们必须对子树的大小进行动态的维护。

对于旋转，我们要在旋转后对子节点和根节点分别重新计算其子树的大小。

对于插入，新建立的节点的子树大小为1。在寻找插入的位置时，每经过一个节点，都要先使以它为根的子树的大小增加1，再递归进入子树查找。

对于删除，在寻找待删除节点，递归返回时要把所有的经过的节点的子树的大小减少1。要注意的是，删除之前一定要保证待删除节点存在于Treap中。

四：查询k是第几大

1.定义P为当前访问的节点，从根节点开始访问，查找排名第k的元素；

2.若满足P.left.size + 1 <=k <= P.left.size + P.weight，则当前节点包含的元素就是排名第k的元素；  

3.若满足k < P.left.size + 1，则在左子树中查找排名第k的元素；

4.若满足k > P.left.size + P.weight，则在右子树中查找排名第k-(P.left.size + P.weight)的元素。

 模板题【bzoj3224】Tyvj 1728 普通平衡树

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：
1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

Input

第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号(1<=opt<=6)

Output

对于操作3,4,5,6每行输出一个数，表示对应答案

Sample Input

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

Sample Output

106465
84185
492737

Hint

1.n的数据范围：n<=100000

2.每个数的数据范围：[-2e9,2e9]

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
using namespace std;
int lson[1000001],rson[1000001],size[1000001],cs[1000001],heap[1000001],val[1000001],cnt=0,ans,root=0;
//左儿子，右儿子，子树大小，出现次数，随机值，该点值 
void up(int x){size[x]=size[lson[x]]+size[rson[x]]+cs[x];}         //我当时打的时候忘记加上自己出现的次数
int lturn(int x){int t=rson[x];rson[x]=lson[t];lson[t]=x;up(x);up(t);return t;}//返回值是深度最低的点的值 
int rturn(int x){int t=lson[x];lson[x]=rson[t];rson[t]=x;up(x);up(t);return t;}//即最上面的值 
int add(int x,int v)//插入一个权值为v的点 ,返回值是该点原父亲的左（右）孩子值 
{
    if(!x){x=++cnt;lson[x]=0;rson[x]=0;size[x]=1;cs[x]=1;heap[x]=rand();val[x]=v;return x;}
    size[x]++;
    if(val[x]==v){cs[x]++;return x;}
    if(val[x]>v){lson[x]=add(lson[x],v);if(heap[lson[x]]<heap[x])return rturn(x);return x;}//递归旋转完了后加入的点变成了x的子树，由于是找左子树，所以右旋
    if(val[x]<v){rson[x]=add(rson[x],v);if(heap[rson[x]]<heap[x])return lturn(x);return x;}
}
int del(int x,int v)//返回值同上 
{
    if(x==0)return x;//没找到 
    if(val[x]==v)//找到 
    {
        if(cs[x]>1){cs[x]--;size[x]--;return x;}
        if(!(lson[x]*rson[x]))return lson[x]+rson[x];//如果左右子树有不为空，删该点       这个括号不能省略（我就这里调了半天）
        int t;
        if(heap[lson[x]]<heap[rson[x]]){t=rturn(x);size[t]--;rson[t]=del(x,v);return t;}//右旋往t的右子树（x)找，更新t右子树
                   //注意要更新t节点的子树大小，因为x变成t的子节点，而x要被删去，所以要把t的子树大小减一
        else {t=lturn(x);size[t]--;lson[t]=del(x,v);return t;}//选左右子树随机值小的旋转至根 
    }
    if(val[x]>v){size[x]--;lson[x]=del(lson[x],v);return x;}//往左找 
    if(val[x]<v){size[x]--;rson[x]=del(rson[x],v);return x;}
}
int get_rank(int x,int v)//查询v是第几大 
{
    if(val[x]==v)return size[lson[x]]+1;
    if(val[x]>v){return get_rank(lson[x],v);} 
    if(val[x]<v){return size[lson[x]]+cs[x]+get_rank(rson[x],v);}
} 
int get_val(int x,int v)//查询第几大的数 
{
    if(v<=size[lson[x]])return get_val(lson[x],v);
    if(v>size[lson[x]]+cs[x])return get_val(rson[x],v-size[lson[x]]-cs[x]);
    return val[x];
}
void get_qq(int x,int v)//找前驱 
{
    if(x==0)return;
    if(val[x]<v){ans=val[x];get_qq(rson[x],v);}
    else get_qq(lson[x],v);
}
void get_hj(int x,int v)//找后继 
{
    if(x==0)return;
    if(val[x]>v){ans=val[x];get_hj(lson[x],v);}
    else get_hj(rson[x],v);
}
int main()
{
    srand((int)time(0));int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int o,x;scanf("%d%d",&o,&x);
        if(o==1){root=add(root,x);}
        if(o==2){root=del(root,x);}
        if(o==3){printf("%d\\n",get_rank(root,x));}
        if(o==4){printf("%d\\n",get_val(root,x));}
        if(o==5){get_qq(root,x);printf("%d\\n",ans);}
        if(o==6){get_hj(root,x);printf("%d\\n",ans);}
    }
    return 0;
 } 

 话说bzoj用srand会RE。。。。。