XJOI 修缮计划(最小生成树,LCA)

Posted 2020-10-05

题面非常简单,给你一张图

一条路径的权是指路径上最长边的权值

询问两个点之间所有路径中权值最小的

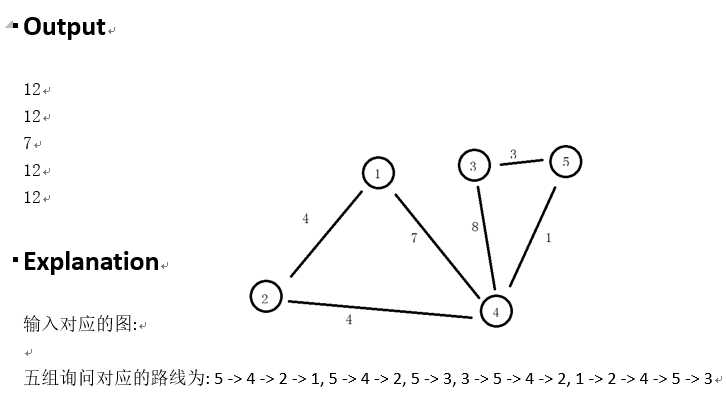
然后我傻乎乎地打了一个暴力SPFA

#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N=10010,M=200010;
int dis[N][N],b[M],c[M],ne[M],fi[N],cc[N],k,x,y,in[N],n,m,z,q;
inline void add(const int &x,const int &y,const int &z){
    b[++k]=y; c[k]=z; ne[k]=fi[x]; fi[x]=k; 
}
inline int max(const int &x,const int &y){
    return x>y?x:y;
}
void SPFA(int s){
    queue<int>q;
    q.push(s);
    dis[s][s]=0;
    while (!q.empty()){
        x=q.front(); q.pop(); in[x]=0;
        for (int j=fi[x]; j; j=ne[j])
        if (max(dis[s][x],c[j])<dis[s][b[j]]){
            dis[s][b[j]]=max(dis[s][x],c[j]);
            if (!in[b[j]]){
                q.push(b[j]);
                in[b[j]]=1;
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i=1; i<=n; i++) scanf("%d",&cc[i]);
    for (int i=1; i<=m; i++){
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z+cc[x]+cc[y]); add(y,x,z+cc[x]+cc[y]);
    }
    memset(dis,0x3f3f3f,sizeof(dis));
    for (int i=1; i<=n; i++) SPFA(i);
    scanf("%d",&q);
    while (q--){
        scanf("%d%d",&x,&y);
        printf("%d\\n",dis[x][y]);
    }
}

考试结束前10分钟才意识到正解,为时已晚.

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#include<cstdlib>
using namespace std;
const int N=10010,M=200010,INF=0x3f3f3f;
struct edge{
    int x,y,z;
}e[M];
int b[M],c[M],ne[M],fi[N],cc[N],fa[N],k,x,y,n,m,z,q,f[N][21],maxf[N][21],deep[N];
inline void add(const int &x,const int &y,const int &z){
    b[++k]=y; c[k]=z; ne[k]=fi[x]; fi[x]=k;
}
bool cmp(edge x,edge y){
    return x.z<y.z;
}
inline int find(int x){
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
void dfs(int x){
    for (int j=fi[x]; j; j=ne[j])
    if (b[j]!=f[x][0]){
        f[b[j]][0]=x;
        maxf[b[j]][0]=c[j];
        deep[b[j]]=deep[x]+1;
        dfs(b[j]);
    }
}
int getlca(int x,int y){
    int res=0;
    if (deep[x]>deep[y]) x^=y^=x^=y;
    for (int j=20; j>=0; j--)
    if (deep[f[y][j]]>=deep[x]){
        res=max(res,maxf[y][j]);
        y=f[y][j];
    }
    if (x==y) return res;
    for (int j=20; j>=0; j--)
    if (f[x][j]!=f[y][j]){
        res=max(max(res,maxf[x][j]),maxf[y][j]);
        x=f[x][j];
        y=f[y][j];
    }
    res=max(res,max(maxf[x][0],maxf[y][0]));
    return res;
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i=1; i<=n; i++) scanf("%d",&cc[i]);
    for (int i=1; i<=m; i++){
        scanf("%d%d%d",&x,&y,&z);
        e[i].x=x;
        e[i].y=y;
        e[i].z=z+cc[x]+cc[y];
    }
    sort(e+1,e+m+1,cmp);
    for (int i=1; i<=n; i++) fa[i]=i;
    for (int i=1; i<=m; i++){
        x=find(e[i].x); y=find(e[i].y);
        if (x!=y){
            fa[x]=y;
            add(e[i].x,e[i].y,e[i].z);
            add(e[i].y,e[i].x,e[i].z);
        }
    }
    dfs(1);
    for (int j=1; j<=20; j++)
    for (int i=1; i<=n; i++){
        f[i][j]=f[f[i][j-1]][j-1];
        maxf[i][j]=max(maxf[i][j-1],maxf[f[i][j-1]][j-1]);
    }
    scanf("%d",&q);
    while (q--){
        scanf("%d%d",&x,&y);
        printf("%d\\n",getlca(x,y));
    }
}

惨啊