算法入门经典第六章 例题6-15 给任务排序

Posted 2020-10-05 Tina

 

假设有n个变量，还有m个二元组（u，v），分别表示变量u小于v。那么，所有变量从小到大排列起来应该是什么样子呢？例如，有4个变量a,b,c,d,若已知a<b,c<b,d<c,则这4个变量的排序可能是a<d<c<b。尽管还有其他可能（如d<a<c<b），你只需找出其中一个即可。

Sample Input

5 4

1 2

2 3

1 3

1 5

0 0

Sample Output

1 4 2 5 3

 

题意：假设有n个变量，还有m个二元组(u,v)，分别表示变量u小于v。那么，所有变量从小到大排列起来应该是什么样子的呢？

把每个变量看成一个点，“小于”关系看成有向边，则得到了一个有向图。这样，我们的任务实际上是把一个图的所有结点排序，使得每一条有向边(u,v)对应的u都排在v的前面。

用dfs完成拓扑排序，在访问完一个结点之后吧它加到当前拓扑序的首部。

 

#include<stdio.h> 
#include<stdlib.h> 
#include<string.h> 
#include<math.h> 
#define max 100+5 
int c[max],topo[max],t,n,G[max][max]; 
//如G[1,2] 从1指向2的有向线段 
int dfs(int u) 
{ 
int v; 
c[u] = -1; //访问标志，-1为正在访问，0是未访问，1是已经访问
for(v = 1; v <= n; v++) //看的是与你比较的v 有无再次访问到 
if(G[u][v]) 
{ 
if(c[v] < 0) return 0; // 如果再次访问到一个在c中被标记为-1的结点就说明存在一个有向环
else if(!c[v] && !dfs(v)) return 0; //v没被访问过 用dfs递归 如果返回0表示失败 


} 
c[u] = 1; 
topo[--t] = u; 
return 1; 
} 
int toposort() 
{ 
int i; 
t = n; 
memset(c,0,sizeof(c)); 
for(i = 1; i <= n; i++) 
if(!c[i] && !dfs(i)) return 0; 
return 1; 
} 
int main() 
{ 
int m,i; 
while(scanf("%d%d",&n,&m),n || m) 
{ 
int u,v; 
memset(G,0,sizeof(G)); 
for(i = 0 ; i < m ; i++) 
{ 
scanf("%d%d",&u,&v); 
G[u][v] = 1; 
} 
if(toposort()) 
{ 
for(i = 0; i < n-1; i++) 
printf("%d ",topo[i]); 
printf("%d\\n",topo[i]); 
} 
} 
return 0; 
}

 

【分析】

题目中n个变量看成图中n个结点，图中的边即是二元关系，m个二元组就代表了这m条边表示的二元关系，（u,v）表示v大于u，从u向v连一条有向边，如果这m个二元
组不矛盾，那么这个图便是一个DAG否则就存在一个有向环，解便不存在了，举个例子a<b,b<c,可以推出a<c，但是现在出现了c连到了a意思是a>c，与之前的递推相
悖，所以如果图中存在有向环，则不存在拓扑序，反之一个DAG图就存在拓扑序，拓扑序可以用DFS求。从图中的某个结点开始，用一个c数组标记，-1表示这个结点正
在访问，那么如果再次访问到一个在c中被标记为-1的结点就说明存在一个有向环，0表示这个结点还未被访问，它的子孙有没有被访问不知道，因为有可能从它的子孙
开始DFS，1表示这个结点以及它的子孙已经被访问过，每次DFS在访问完一个结点后把它加到当前拓扑序首部，因为只能保证向后已经访问完，我们不知道开始DFS的
结点是否有父结点，所以如果前面还有结点肯定都比现在访问到的这些结点要小必须放在它们前面。

【拓展】

有向无环图（Directed Acyclic Graph, DAG）是有向图的一种，字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系，管理任务之间的调度。拓扑排序是对DAG的顶点进行排序，使得对每一条有向边(u, v)，均有u（在排序记录中）比v先出现。亦可理解为对某点v而言，只有当v的所有源点均出现了，v才能出现。

下图给出有向无环图的拓扑排序：

 

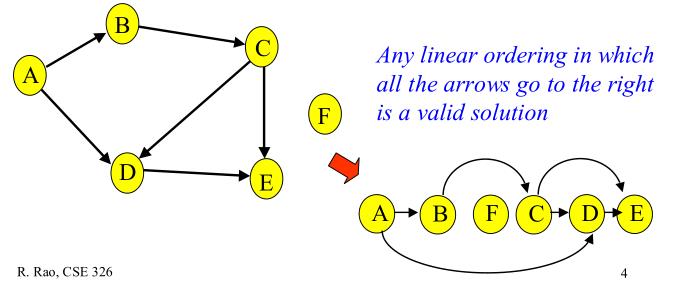
DFS

在DFS中，依次打印所遍历到的顶点；而在拓扑排序时，顶点必须比其邻接点先出现。在下图中，顶点5比顶点0先出现，顶点4比顶点1先出现。

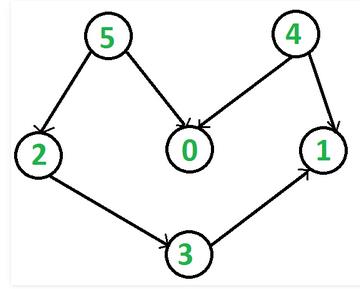
在DFS实现拓扑排序时，用栈来保存拓扑排序的顶点序列；并且保证在某顶点入栈前，其所有邻接点已入栈