python 下的数据结构与算法---6：6大排序算法

Posted 2020-06-29 billiepander

一：冒泡排序（Bubble Sort）

　　原理：假设有n个数，第一轮时：从第一个元素开始，与相邻的元素比较，如果前面的元素小就交换，直到第n-1个元素时，这样的结果是将最大的元素放到了最后，同理，第二轮还是从第一个元素开始比较，直到第n-2个元素，这样能够把剩下的n-1个数中的最大的数放到第n-1的位置，一直这样进行n-1轮就能够完成排序。 

 1 def Bublesort(seq):
 2     i = 0
 3     j = 0
 4     while i < len(seq):
 5         while j < len(seq)-i-1:
 6             if seq[j] > seq[j+1]:
 7                 seq[j],seq[j+1] = seq[j+1],seq[j]
 8             else:
 9                 j+=1
10         j=0
11         i+=1
12 
13 a=[3,4,6,2,1]
14 Bublesort(a)
15 print(a)

冒泡排序

　　由代码可知，其时间复杂度为O(n²).

 

二：选择排序（Selection Sort）

　　原理：选择排序的思路非常简单，每次都遍历找出上次剩下的元素中的最大数，然后和剩下数中随后一个元素交换位置，一个进行n-1次

 1 #coding:utf-8
 2 #Attention:max标志需取为seq[0]，我刚开始取了0，这会导致最后一次比较时出问题
 3 def SelectionSort(seq):
 4     i,j,maxel = 0,0,seq[0]
 5     while i < len(seq):
 6         while j < len(seq)-i:
 7             if seq[j] > maxel:
 8                 maxel = j
 9             j+=1
10         seq[maxel],seq[len(seq)-i-1] = seq[len(seq)-i-1],seq[maxel]
11         j,maxel=0,seq[0]
12         i+=1
13 
14 a=[3,4,6,2,1]
15 SelectionSort(a)
16 print(a)

选择排序

　　可以看出的是，其时间复杂度依然是O(n²),看起来和冒泡排序一样，但由于每轮其交换位置的次数少，故实际上其比冒泡排序好。

 

三：插入排序（Insertion Sort）

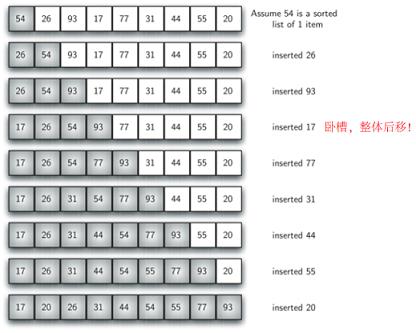
　　原理：如下图所示，将第一个元素作为标准，每次将下一个元素放到前面正确的位置中去。

　　技巧：从已排好序元素最后一个开始遍历比较，因为插入移动只会移动其后面的元素。

　　

 1 def insertion_sort(a_list):
 2     for index in range(1, len(a_list)):
 3         current_value = a_list[index]
 4         position = index
 5         while position > 0 and a_list[position - 1] > current_value:        #从目前元素开始向前，若>目前值就后移一位
 6             a_list[position] = a_list[position - 1]
 7             position = position - 1
 8         a_list[position] = current_value
 9 
10 a = [54, 26, 93, 17, 77, 31, 44, 55, 20]
11 insertion_sort(a)
12 print(a)

插入排序

　　依旧可以看出的是，其时间复杂度为O(n²)，但是他的不同之处在于其始终保持了一个部分有序的序列

 

四：希尔排序（Shell Sort）

　　希尔排序这章书里面的配图不好，导致我理解错误直到运行程序出错才发现错误，后来看了些其他资料弄明白了。其实希尔排序就是跳跃式插入排序，我们试想一下，如果一个元素集是9，8，7，6，5，4，3，2，1，那么每次插入排序都要全部后移了，这样效率极低，如果能够不按顺序的进行插入排序就好多了，虽然每次并没有完全排好序，但是能够让他们离真实的位置更近，这就是其优势所在了。

　　实现原理：每次取一个gap，第一次取集合元素个数整除2的结果，然后对从首元素开始每gap距离的元素组合成一个组并对其进行插入排序，假设集合[54, 26, 93, 17, 77, 31, 44, 55, 20]，那么第一次gap为9//2=4，那么就能够有这些组：[54,77,20],[26,31],[93,44],[17,55],注意，并不是对其真的分组，只是将其看作一组后进行插入排序，那么结果是：[20, 26, 44, 17, 54, 31, 93, 55, 77],到此，第一次完成。第二次把gap改为上次gap//2的结果，也就是2，所以对上次的结果分组为[20,44,54,93,77],[26,17,31,55],对其进行插入排序后的结果是[20, 17, 44, 26, 54, 31, 77, 55, 93]，到此第二次完成。第三次gap为1，注意，当gap为1时就表明是最后一轮了，最上此结果[20, 17, 44, 26, 54, 31, 77, 55, 93]全部进行插入排序就能够得到结果了。【仔细看看就能够发现其每次排序后真的是数字离其真实位置更近了】。

　　注意：有个控制循环的条件就是每次分组的组数其实就是gap的值，容易看出是两层控制，外层控制进入的哪组分组，内层控制具体每组的插入排序

 1 def shell_sort(a_list):
 2     sublist_count = len(a_list) // 2
 3     while sublist_count > 0:
 4         for start_position in range(sublist_count):
 5             gap_insertion_sort(a_list, start_position, sublist_count)
 6         print("After increments of size", sublist_count, "The list is",a_list)
 7         sublist_count = sublist_count // 2
 8 
 9 def gap_insertion_sort(a_list,start, gap):
10     for i in range(start + gap, len(a_list), gap):
11         current_value = a_list[i]
12         position = i
13         while position >= gap and a_list[position - gap] > current_value:
14             a_list[position] = a_list[position - gap]
15             position = position - gap
16         a_list[position] = current_value
17 
18 a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
19 shell_sort(a_list)
20 print(a_list)

希尔排序

　　

 五:归并排序（Merge Sort）

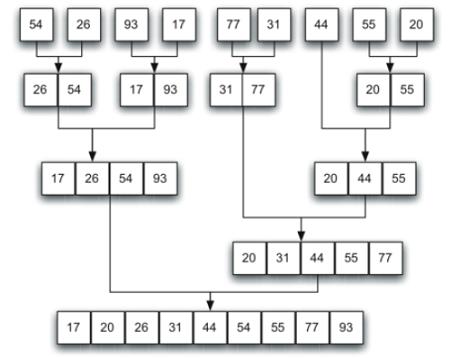
　　原理图：由图可以看出，其也是用了递归原理，base就是只剩一个元素时返回其本身

　　

 1 def partition(seq, start, mid, stop):
 2     lst = []
 3     i = start
 4     j = mid
 5     while i < mid and j < stop:
 6         if seq[i] < seq[j]:
 7             lst.append(seq[i])
 8             i+=1
 9         else:
10             lst.append(seq[j])
11             j+=1
12     while i < mid:
13         lst.append(seq[i])
14         i+=1
15     while j < stop:
16         lst.append(seq[j])
17         j+=1
18     for i in range(len(lst)):
19         seq[start+i]=lst[i]
20 
21 def mergeSortRecursively(seq, start, stop):
22     if start >= stop-1:
23         return
24     mid = (start + stop) // 2
25     mergeSortRecursively(seq, start, mid)
26     mergeSortRecursively(seq, mid, stop)
27     partition(seq, start, mid, stop)
28 
29 a=[3,4,6,8,2,1,5,9]
30 mergeSortRecursively(a, 0, len(a))
31 print(a)

归并排序

　　来分析下其时间复杂度吧，由于每次都将list二分，这是logn，而每次排列是n，由于这两小步组成一步，故时间复杂度为O(nlogn)

 

六：快速排序（Quick Sort）

　　原理：如下，第一次以第一个元素为标志，将后面小的放他左边，大的放他右边，而后将其放到中间。第二次分别在其两边重复这样的过程，最后直到每组只有一个数据。

　　

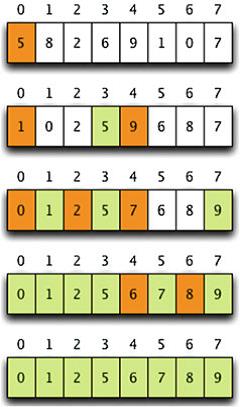
　　有个需要注意的是最坏情况下为以排好序的集合，那么后面的数都标志大或者小，操作太多或者无效，最理想的是标志能够是平均值左右，故最好对数据进行随机化处理。

　　还有，看完代码后注意比较，可以是快速排序与归并排序是某种程度相反的，归并到了最后两个元素才开始排序，从部分有序积累到全部有序，而二分是反的，从第一次二分就是整个数列的二分，，最后二分到只有两个元素时，此时完成了全部有序。

 1 import random
 2 def partition(seq, start, stop):
 3     pivotIndex = start
 4     pivot = seq[pivotIndex]
 5     i = start+1
 6     j = stop-1 
 7     while i <= j:
 8         while pivot > seq[i]:
 9             i+=1
10         while pivot < seq[j]:
11             j-=1
12         if i < j:
13             seq[j],seq[i] = seq[i],seq[j]
14             i+=1
15             j-=1
16     seq[pivotIndex],seq[j] = seq[j],pivot
17     return j
18 
19 def quicksortRecursively(seq, start, stop):
20     if start >= stop-1:
21         return
22     pivotIndex = partition(seq, start, stop)
23     quicksortRecursively(seq, start, pivotIndex)
24     quicksortRecursively(seq, pivotIndex+1, stop)
25 
26 def quicksort(seq):
27 # randomize the sequence first
28     for i in range(len(seq)):
29         j = random.randint(0,len(seq)-1)
30         seq[i],seq[j] = seq[j],seq[i]
31 
32     quicksortRecursively(seq, 0, len(seq))
33 
34 a=[3,4,6,8,2,1,5,9]
35 quicksort(a)
36 print(a)

快速排序

　　同理可以分析出其时间复杂度为O(nlogn)