追踪电子表格中的单元格
Posted Not-Bad
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了追踪电子表格中的单元格相关的知识，希望对你有一定的参考价值。
| Spreadsheet Tracking |
Data in spreadsheets are stored in cells, which are organized in rows (r) and columns (c). Some operations on spreadsheets can be applied to single cells (r,c), while others can be applied to entire rows or columns. Typical cell operations include inserting and deleting rows or columns and exchanging cell contents.
Some spreadsheets allow users to mark collections of rows or columns for deletion, so the entire collection can be deleted at once. Some (unusual) spreadsheets allow users to mark collections of rows or columns for insertions too. Issuing an insertion command results in new rows or columns being inserted before each of the marked rows or columns. Suppose, for example, the user marks rows 1 and 5 of the spreadsheet on the left for deletion. The spreadsheet then shrinks to the one on the right.
 |
 |
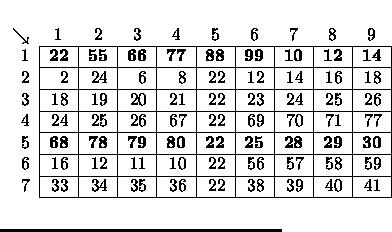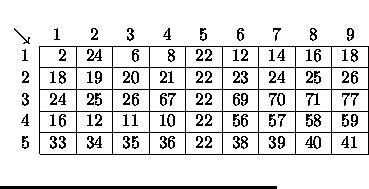If the user subsequently marks columns 3, 6, 7, and 9 for deletion, the spreadsheet shrinks to this.
 |
1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 24 | 8 | 22 | 16 |
| 2 | 18 | 19 | 21 | 22 | 25 |
| 3 | 24 | 25 | 67 | 22 | 71 |
| 4 | 16 | 12 | 10 | 22 | 58 |
| 5 | 33 | 34 | 36 | 22 | 40 |
If the user marks rows 2, 3 and 5 for insertion, the spreadsheet grows to the one on the left. If the user then marks column 3 for insertion, the spreadsheet grows to the one in the middle. Finally, if the user exchanges the contents of cell (1,2) and cell (6,5), the spreadsheet looks like the one on the right.
 |
 |
 |
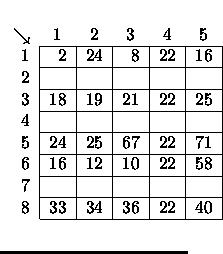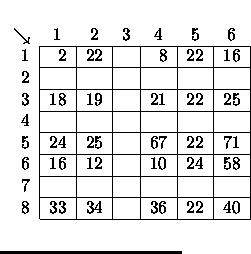You must write tracking software that determines the final location of data in spreadsheets that result from row, column, and exchange operations similar to the ones illustrated here.
Input
The input consists of a sequence of spreadsheets, operations on those spreadsheets, and queries about them. Each spreadsheet definition begins with a pair of integers specifying its initial number of rows ( r) and columns ( c), followed by an integer specifying the number (n) of spreadsheet operations. Row and column labeling begins with 1. The maximum number of rows or columns of each spreadsheet is limited to 50. The following n lines specify the desired operations.
An operation to exchange the contents of cell (r1, c1) with the contents of cell (r2, c2) is given by:
EXr1c1r2c2
The four insert and delete commands--DC (delete columns), DR (delete rows), IC (insert columns), and IR (insert rows) are given by:
< command> Ax1x2
xA
where <command> is one of the four commands; A is a positive integer less than 10, and 
are the labels of the columns or rows to be deleted or inserted before. For each insert and delete command, the order of the rows or columns in the command has no significance. Within a single delete or insert command, labels will be unique.
The operations are followed by an integer which is the number of queries for the spreadsheet. Each query consists of positive integers rand c, representing the row and column number of a cell in the original spreadsheet. For each query, your program must determine the current location of the data that was originally in cell (r, c). The end of input is indicated by a row consisting of a pair of zeros for the spreadsheet dimensions.
Output
For each spreadsheet, your program must output its sequence number (starting at 1). For each query, your program must output the original cell location followed by the final location of the data or the word GONE if the contents of the original cell location were destroyed as a result of the operations. Separate output from different spreadsheets with a blank line.
The data file will not contain a sequence of commands that will cause the spreadsheet to exceed the maximum size.
Sample Input
7 9 5 DR 2 1 5 DC 4 3 6 7 9 IC 1 3 IR 2 2 4 EX 1 2 6 5 4 4 8 5 5 7 8 6 5 0 0
Sample Output
Spreadsheet #1 Cell data in (4,8) moved to (4,6) Cell data in (5,5) GONE Cell data in (7,8) moved to (7,6) Cell data in (6,5) moved to (1,2)
模拟删除，交换，插入行或列的操作后，查询原始表格中数据在现在表格中对应的位置。
以下代码玩的是数组，各种数组各种存储信息！
首先模拟操作，算出最后的表格，然后每次查询直接找到即可
#include<iostream> #include<cstdio> #include<string.h> using namespace std; #define maxd 100 #define BIG 10000 int r,c,n,d[maxd][maxd],d2[maxd][maxd],ans[maxd][maxd],cols[maxd]; //r行c列的表格，n个操作指令，d存储表格中的标识数据，改变d void copy(char type,int p,int q) //将新插入的或不删除的那组数copy到新表格中 { //p为要改变的表d中按顺序排列的数组，q为d2表中不删除的数组 if(type==‘R‘){ for(int i=1;i<=c;i++)d[p][i]=d2[q][i]; } else{ for(int i=1;i<=r;i++)d[i][p]=d2[i][q]; } } void del(char type) { memcpy(d2,d,sizeof(d)); int cnt=type==‘R‘?r:c,cnt2=0; //如果是删除行即type==‘R‘,就给cnt赋值为行数，否则为列数 for(int i=1;i<=cnt;i++){ if(!cols[i])copy(type,++cnt2,i); //将不删除的数copy到新表格中 } if(type==‘R‘)r=cnt2; //删除后行列变少 else c=cnt2; } void ins(char type) { memcpy(d2,d,sizeof(d)); //d2用来储存原始数据来改变d int cnt=type==‘R‘?r:c,cnt2=0; for(int i=1;i<=cnt;i++){ if(cols[i])copy(type,++cnt2,0); //新插入数组的数组赋值为d[i][0]或d[0][j] copy(type,++cnt2,i); } if(type==‘R‘)r=cnt2; else c=cnt2; } int main() { int r1,c1,r2,c2,q,kase=0; char cmd[10]; memset(d,0,sizeof(d)); while(scanf("%d%d%d",&r,&c,&n)==3&&r){ int r0=r,c0=c; for(int i=1;i<=r;i++) //把d[i][0]和d[0][j]留为新插入行和列的赋值 for(int j=1;j<=c;j++)d[i][j]=i*BIG+j; //给各个位置的元素赋一个特定的值，如 第一行第二列的值为10002 while(n--){ scanf("%s",cmd); if(cmd[0]==‘E‘){ //交换 scanf("%d%d%d%d",&r1,&c1,&r2,&c2); int t=d[r1][c1]; //交换两值即可 d[r1][c1]=d[r2][c2]; d[r2][c2]=t; } else{ int a,x; scanf("%d",&a); memset(cols,0,sizeof(cols)); for(int i=0;i<a;i++){ scanf("%d",&x); cols[x]=1; //将要删除或者插入的(多个)第a行或第a列的数据赋值为1 } if(cmd[0]==‘D‘)del(cmd[1]); //删除 else ins(cmd[1]); //插入 } } memset(ans,0,sizeof(ans)); //用来存储变化 for(int i=1;i<=r;i++) for(int j=1;j<=c;j++){ ans[d[i][j]/BIG][d[i][j]%BIG]=i*BIG+j; //d与ans反着存储着，如d[1][1]=20001,则ans[2][1]=10001,原本2行1列的元素现在在1行1列 printf("d[%d][%d] %d\n",i,j,d[i][j]); printf("ans[%d][%d] %d\n",d[i][j]/BIG,d[i][j]%BIG,i*BIG+j); } if(kase>0)printf("\n"); printf("Spreadsheet #%d\n",++kase); scanf("%d",&q); while(q--){ scanf("%d%d",&r1,&c1); printf("Cell data in (%d,%d) ",r1,c1); if(ans[r1][c1]==0)printf("GONE\n"); else printf("moved to (%d,%d)\n",ans[r1][c1]/BIG,ans[r1][c1]%BIG); } } //system("pause"); return 0; }
另一种思路是将所有的操作保存，然后对于每个查询重新执行每个操作，但不需要计算整个表格的变化，而只需要关注所查询的单元格的位置变化。
这种方法对于题目给的规模，即好写，效率又高。
明显好理解！！！
#include<iostream> #include<cstdio> #include<string.h> using namespace std; #define maxd 10000 struct Command{ char c[5]; int r1,c1,r2,c2; int a,x[20]; }cmd[maxd]; int r,c,n; int simulate(int* r0,int* c0) { for(int i=0;i<n;i++){ //n次变换 if(cmd[i].c[0]==‘E‘){ if(cmd[i].r1==*r0&&cmd[i].c1==*c0){ *r0=cmd[i].r2; *c0=cmd[i].c2; } else if(cmd[i].r2==*r0&&cmd[i].c2==*c0){ *r0=cmd[i].r1; *c0=cmd[i].c1; } } else{ int dr=0,dc=0; for(int j=0;j<cmd[i].a;j++){ int x=cmd[i].x[j]; //x[j]为变化的行数或列数 if(cmd[i].c[0]==‘I‘){ if(cmd[i].c[1]==‘R‘&&x<=*r0)dr++; if(cmd[i].c[1]==‘C‘&&x<=*c0)dc++; } else{ if(cmd[i].c[1]==‘R‘&&x==*r0)return 0; //删除掉了 if(cmd[i].c[1]==‘C‘&&x==*c0)return 0; if(cmd[i].c[1]==‘R‘&&x<*r0)dr--; if(cmd[i].c[1]==‘C‘&&x<*c0)dc--; } } *r0+=dr; *c0+=dc; } } return 1; } int main() { int r0,c0,q,kase=0; while(scanf("%d%d%d",&r,&c,&n)==3&&r){ for(int i=0;i<n;i++){ scanf("%s",cmd[i].c); if(cmd[i].c[0]==‘E‘){ scanf("%d%d%d%d",&cmd[i].r1,&cmd[i].c1,&cmd[i].r2,&cmd[i].c2); } else{ scanf("%d",&cmd[i].a); for(int j=0;j<cmd[i].a;j++)scanf("%d",&cmd[i].x[j]); } } if(kase>0)printf("\n"); printf("Spreadsheet #%d\n",++kase); scanf("%d",&q); while(q--){ scanf("%d%d",&r0,&c0); printf("Cell data in(%d,%d) ",r0,c0); if(!simulate(&r0,&c0))printf("GONE\n"); else printf("moved to (%d,%d)\n",r0,c0); } } // system("pause"); return 0; }
以上是关于追踪电子表格中的单元格的主要内容，如果未能解决你的问题，请参考以下文章
Open XML SDK 2.0 - 如何更新电子表格中的单元格？