CCF系列之最大的矩形(201312-3)

Posted 2020-06-29 一只猫的旅行

试题名称： 最大的矩形

时间限制： 1.0s 

内存限制： 256.0MB 

问题描述：　

问题描述

　　在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是h_i。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。



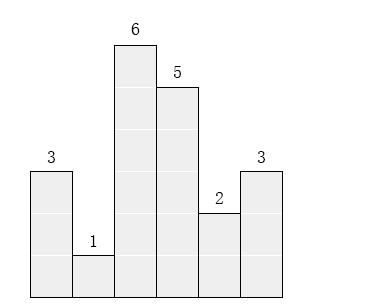
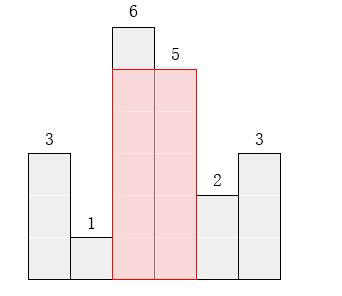
　　请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。

输入格式

　　第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h₁, h₂, … , h_n，相邻的数之间由空格分隔。(1 ≤ h_i ≤ 10000)。h_i是第i个矩形的高度。

输出格式

　　输出一行，包含一个整数，即给定直方图内的最大矩形的面积。

样例输入

6
3 1 6 5 2 3

样例输出

10

解题思路:　

代码如下（java）：

 1 package ccf_text2013_12;
 2 
 3 import java.util.Scanner;
 4 /**
 5  * 最大的矩形
 6  * @author Hello stranger
 7  *
 8  */
 9 public class BiggestRectangle {
10     
11     public static void main(String[] args) {
12         
13         new BiggestRectangle().run();
14         
15     }
16 
17     private void run() {
18         
19         Scanner fin = new Scanner(System.in);
20         
21         int N = fin.nextInt();
22         
23         int[] height = new int[N];
24         
25         for(int i = 0; i < N; i++){
26                         
27             height[i] = fin.nextInt();
28             
29         }
30         
31         //long start = System.nanoTime(); //获取当前系统毫秒值
32         
33         int result = 0;
34         
35         
36         for(int i = 0; i < N; ++i){
37             
38             int width = 1;
39             
40             for(int j = i - 1; j >= 0; --j){
41                 
42                 if(height[j] >= height[i]){
43                     
44                     ++width;
45                     
46                 }else{
47                     
48                     break;
49                 }
50             }
51             
52             for(int j = i + 1; j < N; ++j){
53                 
54                 if(height[j] >= height[i]){
55                     
56                     ++width;
57                     
58                 }else{
59                     
60                     break;
61                 }
62             }
63             
64             int area = width * height[i];
65             
66             result = Math.max(result, area);
67         }
68         
69         System.out.println(result);
70         
71         //long end = System.nanoTime();
72         
73         //System.out.println((end - start)/1.0e9 +"s");
74     }
75     
76 }

 

 

另一个失败代码（java）

 1 package ccf_text2013_12;
 2 
 3 import java.util.Scanner;
 4 /**
 5  * 最大的矩形2（时间不符合）
 6  * @author Hello stranger
 7  *
 8  */
 9 public class BiggestRectangle2 {
10     
11     public static void main(String[] args) {
12         
13         new BiggestRectangle2().run();
14         
15     }
16 
17     private void run() {
18         
19         Scanner fin = new Scanner(System.in);
20         
21         int N = fin.nextInt();
22         
23         int[] height = new int[N];
24         
25         for(int i = 0; i < N; i++){
26                         
27             height[i] = fin.nextInt();
28             
29         }
30         
31         
32         int result = 0;
33         
34         int maxArea = 0;
35         
36         for(int i = 0; i < N; ++i){
37             
38             int high = height[i];
39             
40             for(int j = i + 1; j < N; j++){
41                 
42                 int width = j - i;
43                 
44                 if(high > height[j]){
45                     
46                     high =  height[j];
47                     
48                     width++;
49                     
50                     result = high * width;
51                     
52                 }
53                 if(maxArea < result){
54                     
55                     maxArea = result;
56                 }
57             }
58             
59         }
60         
61         System.out.println(maxArea);
62         
63     }
64     
65 }