堆之二叉堆

Posted 2020-10-04 乘风有时

堆的定义

堆通常是一个可以被看做一棵树，它满足下列性质：

• 堆中任意节点的值总是不大于(不小于)其子节点的值；
• 堆总是一棵完全树。

将任意节点不大于其子节点的堆叫做最小堆或小根堆，而将任意节点不小于其子节点的堆叫做最大堆或大根堆。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。

二叉堆

堆有两种性质：结构性和堆序性

结构性：堆是一颗完全二叉树。若设完全二叉树的高度是h，则它的节点数是2^h到2^(h+1) - 1；则节点数为N的完全二叉树的高度O(logn)。

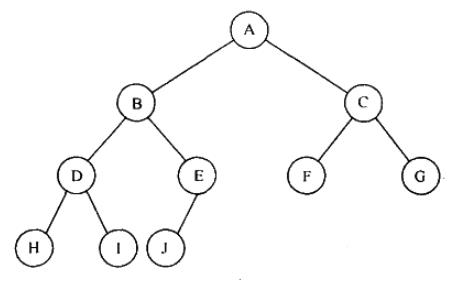
完全二叉树中父子节点位置关系：

• 索引为i的左孩子的索引是 (2*i);
• 索引为i的左孩子的索引是 (2*i+1);
• 索引为i的父结点的索引是 floor(i/2);

则堆也可以使用数组来表示

堆序性：堆一般分为最大堆和最小堆；最大堆的树根为最大的元素，最小堆的树根为最小的元素；这样就能立刻得到树的最大值或最小值。

最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

插入

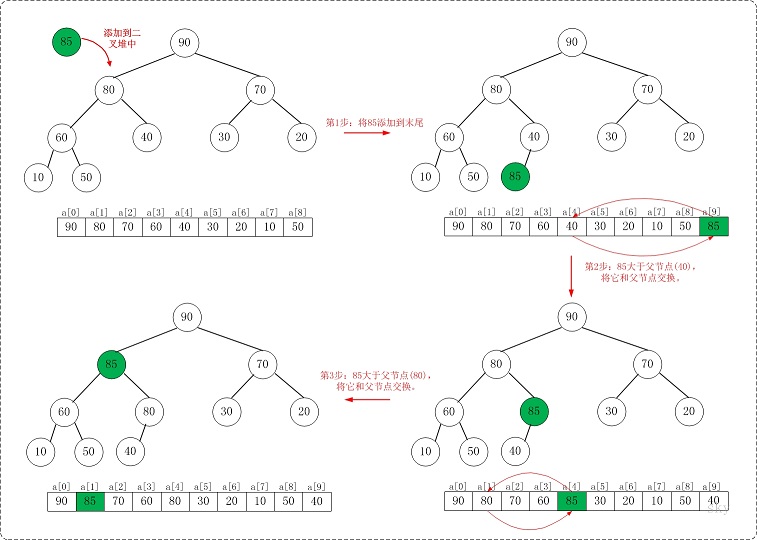
首先，将新元素插入到堆的末尾，这样可能破坏了堆的特性；因此接下来需要调整堆。

（最大堆）调整的方法：自底向上，比较新插入的元素和它的父节点的值，如果新插入的值较大，将新插入的值和父节点交换；然后递归比较父节点的父节点的值，直到新插入的节点到达树根或者新插入的节点的值小于父节点的值。

最大堆[90,80,70,60,40,30,20,10,50]中插入85，过程如下：

简单的实现如下：

void insertMaxHeap(vector<int> &heap, int val){
    heap.push_back(val);
    int p = heap.size() - 1;
    while (p){
        int i = (p - 1) / 2;//父节点的位置
        if (heap[i] < val){//大于父节点交换
            swap(heap[i], heap[p]);
            p = i;
        }
        else break;
    }
}

调整堆的过程称作上滤，它的复杂度O(logn)

删除

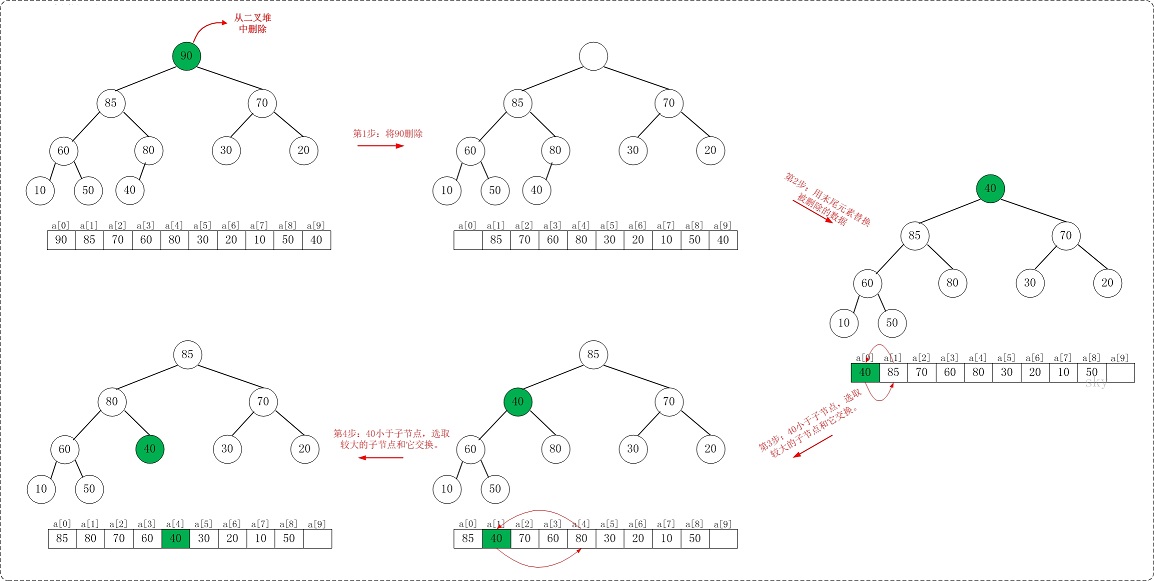
首先说明删除最大元素（最大堆）的过程：

首先将最后的元素和树根元素交换，自顶向下，比较树根和左右孩子的值，选择较大的和树根交换，然后递归找到交换后的节点的孩子，比较它和左右孩子的值找到较大的接着交换，直到到达叶节点。

例如：从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90

实现如下：

void deleteMaxHeap(vector<int> &heap){
    swap(heap[0], heap[heap.size() - 1]);//和最后一个元素交换
    heap.pop_back();//删除最大值
    int p = 0;
    while (p < heap.size()){
        int i = p * 2 + 1;//左孩子的位置
        if (i >= heap.size())break;//无孩子
        else if (i + 1 == heap.size()){//无右孩子
            if (heap[i] > heap[p]){
                swap(heap[p], heap[i]);
                p = i;
            }
            else break;
        }
        if (heap[i] >= heap[i + 1] && heap[i] > heap[p]){//和左孩子交换
            swap(heap[p], heap[i]);
            p = i;
        }
        else if (heap[i] < heap[i + 1] && heap[i + 1] > heap[p]){//和右孩子交换
            swap(heap[p], heap[i + 1]);
            p = i + 1;
        }
        else break;
    }
}

如果是删除任意的节点，可以提高该节点的值，使它变成最大，然后调整堆，使它位于树根，然后就跟删除最大值一样了。

应用

二叉堆用于实现优先队列。

使用优先队列的问题很多：

The Skyline Problem

Top K Frequent Elements

Find K Pairs with Smallest Sums

Kth Smallest Element in a Sorted Matrix