一些排序算法的C++实现

Posted 2020-06-29

一、先定义一个类，方便以后开挖掘机！刚接触面向对象不久，顺便拿来练练手，就当是用东风21-D打蚊子了。

傻乎乎的类：（据我暂时所知，C++里好像没有能获取数组长度的函数“I‘m angry!”。所以手动写个setLength()及getLength()。）

class Arrays{
private:
    int length;  //用来记录数组的长度
    double timeConsume; //记录排序时间，比较算法优越性
    int *array;
    int heap_size; //堆排序中要用到
public:
    void setLength(int theLength)
    {
        length = theLength;
    }
    int getLength()
    {
        return length;
    }
    void setHeap_size(int heap_size)
    {
        this->heap_size = heap_size;
    }
    int getHeap_size()
    {
        return heap_size;
    }
    void setTimeConsume(double time)
    {
        timeConsume = time;
    }
    double getTimeConsume()
    {
        return timeConsume;
    }
    void setArrayEmpty()
    {
        array = new int[length];
    }
    void setArray()
    {
        array = new int[length];
        for (int i = 0; i < length; ++i)
        {
            array[i] = rand()%100000000;
        }
    }
    void setArrayByInput()
    {
        array = new int[length];
        for (int i = 0; i < length; ++i)
        {
            printf("Input one by one.");
            cin >> array[i];
        }
}

二、插入排序

先来个简单点的插入排序，嘿嘿，比较好欺负。

中心思想：对一个数组 A[n]，假设 A[j]为待插入的数组元素，在 for 循环(循环变量为 j)的每次迭代的开始，包含元素 A[1…j-1]的子数组构成了左侧已经排序好的元素，剩余的字数组 A[j+1…n]对应于未被排序的元素，为找到 A[j]对应的位置，对 A[1…j-1]从右向左进行比较(循环变量为 i)，并将 A[i]不断向右移，直到找到元素 A[i]<=A[j],然后将 A[j]置于 A[i+1]处。

Arrays* Insertion_sort(Arrays* testArray)
{
    int key, j;
    for (int i = 1; i < testArray->getLength(); ++i)
    {
        key = testArray->getArray()[i];
        j = i - 1;
        while ((j >= 0) && (testArray->getArray()[j] > key))
        {
            testArray->getArray()[j + 1] = testArray->getArray()[j];
            j--;
        }
        testArray->getArray()[j + 1] = key;
    }
    return testArray;
}

三、归并排序

这个要用到分治法的思想（话说我第一眼看到这个名字还以为是分冶法！看来毕业后当不成程序员要去大炼钢铁了！咱们工人有力量！）

归并算法的核心就是将已排序序列的合并。归并排序分为三个主要步骤：

(a)分解：分解待排序的 n 个元素的序列程各具 n/2 个元素的两个子序列

(b)解决：使用归并排序递归的跑徐两个子序列

(c)合并：合并两个已排序的子序列。

void Merge(Arrays* testArray, int begin, int middle, int end)
{
    int n1 = middle - begin + 1;
    int n2 = end - middle;
    int* L = new int[n1 + 1];
    int* R = new int[n2 + 1];
    for (int i = 0; i < n1; ++i)
    {
        L[i] = testArray->getArray()[begin + i];
    }
    for (int i = 0; i < n2; ++i)
    {
        R[i] = testArray->getArray()[middle + i + 1];
    }
    L[n1] = 9999999;   //999999不是666666反过来，只是设定一个比较大的数而已，可看做无穷
    R[n2] = 9999999;   //同上
    int i = 0, j = 0;
    for (int k = begin; k <= end; ++k)
    {
        if (L[i] <= R[j])
        {
            testArray->getArray()[k] = L[i];
            i++;
        }
        else
        {
            testArray->getArray()[k] = R[j];
            j++;
        }
    }
}
Arrays* Merge_sort(Arrays* testArray, int begin, int end)
{
    if (begin < end)
    {
        int flag = (begin + end) / 2;
        Merge_sort(testArray, begin, flag);
        Merge_sort(testArray, flag + 1, end);
        Merge(testArray, begin, flag, end);
    }
    return testArray;
}

四、堆排序

狂拽酷炫吊炸天！又一个分治法的典范！膜。要懂一些二叉树的思想。

堆是一个数组，可以被看成一个近似的完全二叉树，树上的每一个节点对应数组中的一个元素。堆排序算法主要过程：先将数组 A[1…n]建成最大堆，此时最大元素在根节点 A[1]中，将其与 A[heap-size]进行互换，另 heap-size=heap-size-1,此时对 A[1….heap-size]维护其最大堆的性质。直至 heap-size 将至 2 为止。

int Parent(int i)  //此处i为下标+1，因为数组是从零开始计数，在这里我们先假设是从一开始计数，这样比较方便得到父节点，左右孩子节点的下标
{
    return i / 2; //返回值也为下标+1，返回父节点下标
}
int Left(int i)
{
    return 2 * i; //返回左孩子节点下标
}
int Right(int i) 
{
    return 2 * i + 1;  //右孩子节点下标
}
void Max_Heapify(Arrays* testArray, int i) //此处i为下标
{
    int l = Left(i + 1) - 1;  //l为数组下标
    int r = Right(i + 1) - 1;  //r为数组下标
    int largest;
    if ((l < testArray->getHeap_size()) && (testArray->getArray()[l] > testArray->getArray()[r]))
        {
            largest = l; //largest为数组下标
        }
    else
    {
        largest = i;
    }
    if ((r < testArray->getHeap_size()) && (testArray->getArray()[r] > testArray->getArray()[largest]))
    {
        largest = r; //largest为数组下标
    }
    if (largest != i)
    {
        int temp = testArray->getArray()[i];
        testArray->getArray()[i] = testArray->getArray()[largest];
        testArray->getArray()[largest] = temp;
        Max_Heapify(testArray, largest);
    }
}
void Build_Max_Heap(Arrays* testArray)
{
    testArray->setHeap_size(testArray->getLength());
    for (int i = testArray->getLength() / 2 - 1; i >= 0; i--)
    {
        Max_Heapify(testArray,i);
    }
}
void Heapsort(Arrays* testArray)
{
    Build_Max_Heap(testArray);
    int temp;
    for (int i = testArray->getLength() - 1; i >= 1; i--)
    {
        temp = testArray->getArray()[0];
        testArray->getArray()[0] = testArray->getArray()[i];
        testArray->getArray()[i] = temp;
        testArray->setHeap_size(testArray->getHeap_size()-1);
        Max_Heapify(testArray, 0);
    }
}

五、随机快速化排序

快速排序的随机化版本，其实就是每次获取主元之前随机生成一个主元罢了，听起来好厉害的样子，不废话，上代码！

随机快速排序：快速排序：数组 A[p....r]被划分为两个字数组 A[p....q-1]和 A[q+1....r]使得 A[p...q-1]中每一个元素都小于 A[q]，A[q+1....r]中每一个元素都大于 A[q]，通过递归调用快速排序，对 A[p...q-1]和 A[q+1...r]进行排序。因字数组都是原址排序的，故无需进行合并操作。而对于随机快速排序，将 A[r]与从 A[p...r]中随机选出的一个元素交换。

int Partition(Arrays* testArray, int p, int r) //p,r均为下标
{
    int x = testArray->getArray()[r];
    int i = p - 1;
    int temp;
    for (int j = p; j < r; ++j)
    {
        if (testArray->getArray()[j] <= x)
        {
            i++;
            temp = testArray->getArray()[i];
            testArray->getArray()[i] = testArray->getArray()[j];
            testArray->getArray()[j] = temp;
        }
    }
    temp = testArray->getArray()[i + 1];
    testArray->getArray()[i+1] = testArray->getArray()[r];
    testArray->getArray()[r] = temp;
    return i + 1;
}
int Randomized_partition(Arrays* testArray, int p, int r)//p,r均为下标
{
    int i = rand() % (r - p + 1) + p;
    int temp = testArray->getArray()[r];
    testArray->getArray()[r] = testArray->getArray()[i];
    testArray->getArray()[i] = temp;
    return Partition(testArray, p, r);
}
void Randomized_quicksort(Arrays* testArray, int p, int r)
{
    if (p < r)
    {
        int q = Randomized_partition(testArray, p, r);
        Randomized_quicksort(testArray, p, q - 1);
        Randomized_quicksort(testArray, q + 1, r);
    }
}

 

 

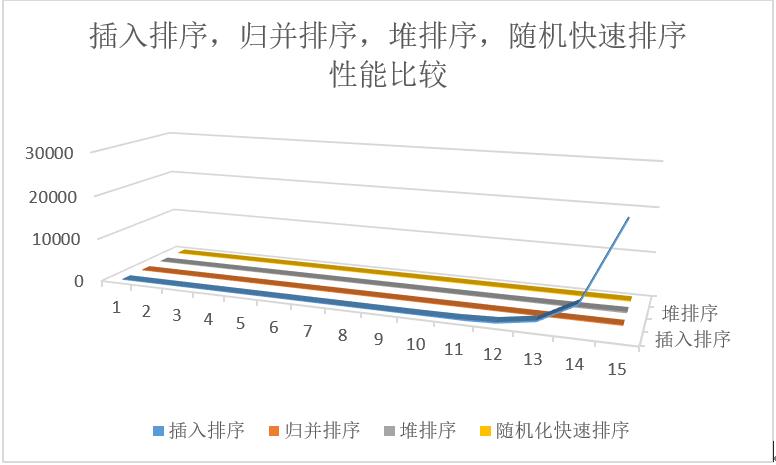
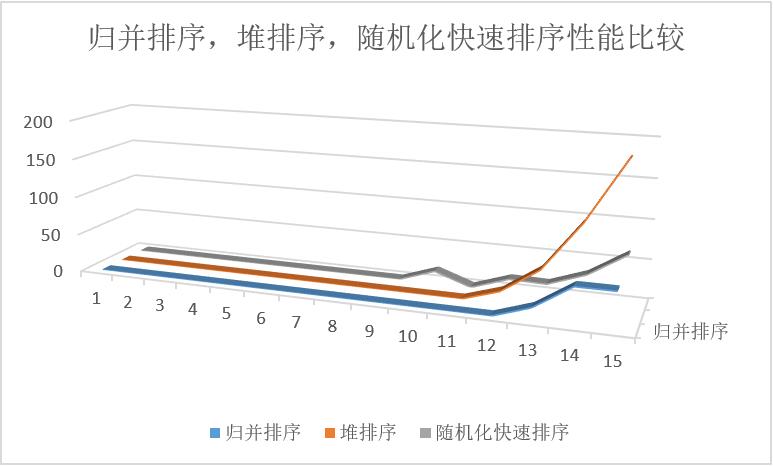
注：纵坐标为时间（毫秒），横坐标为log₂（数据量）。

　未完待续。。。。。

思想来源于《算法导论》这本厚and黑的书，我只是实现了他的伪代码而已。

如果时间充足以后把主函数的部分也贴上去，顺便做一个时间复杂度的比较，通过实际操作来表现大量数据实际排序的优劣对比。