Demystify 稳定匹配理论和圈圈图

Posted 2020-10-04

你知道这个图的意义吗？

 

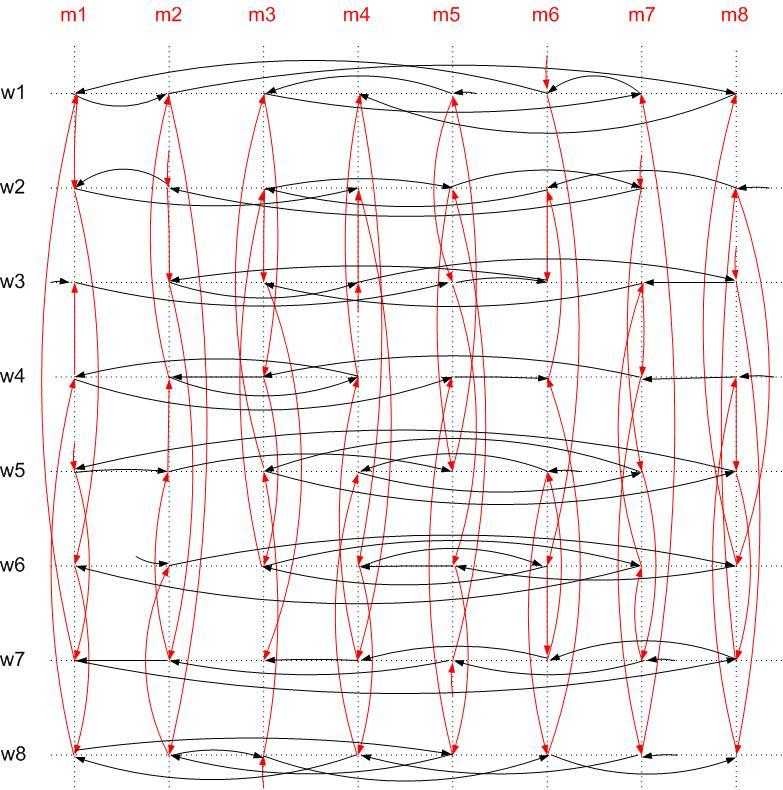
实验经济学里有个人物Al Roth，2012年获得诺贝尔经济奖，获奖领域是稳定匹配理论及其应用。

稳定匹配啥意思？考虑一个虚拟的雇佣市场问题，N个企业和N个工人的一对一匹配问题，假设每个企业对每个工人都有一个打分，分数越高代表某企业在可能的情况下会优先选择那个工人。同样，每个工人也给每个企业打分。现在如何给这些工人和企业做一个一对一的匹配？这是一个双向选择问题，一个公平的匹配应该是稳定匹配，具有如下特性：稳定匹配中的双方，尽管对方未必是最中意的那个，但他（它）又无法和任何另一企业（工人）看对眼，要么他（它）更喜欢其当前匹配的企业（工人），要么另一方更喜欢它的当前匹配的对象。

Al Roth的主要得奖工作是稳定匹配理论的基础，以及实际应用。

稳定匹配问题有个特点，就是，一个匹配对是否稳定，并不仅仅是这两者间的事，而是依赖于其所处的环境。这是典型的局部影响全局，而全局又反过来影响局部的问题。举个现实生活中的例子，一对夫妻M1和F1，在一个地方生活，本来和睦和睦，突然，邻居搬来另一对M2和F2，然后，M1和F2对上眼了，这些原来和睦的婚姻就出裂痕了。

在Roth之后，稳定匹配理论又有许多发展。其方向之一是求解最佳匹配。尽管稳定匹配相对一个随意的匹配方案较为公平，但仍然不是最佳方案。获得最佳方案的办法之一是，在所有的稳定匹配中选优，步骤是，对一个匹配中的所有工人和企业求和，这个和是他（它）的当前匹配的对方在他（它）的优先序列中的名次的和，这个和称为不满意度和。最佳方案之一就是不满意度和最小的那个匹配方案，最佳方案之二是对所有的工人或企业分别计算和，然后计算这两个和的差，选择该差值最小的那个方案为最优方案。。。。

一个课题是，给出一个算法，能够计算上述最佳方案，并且，计算度不高于O（N3)。前面那个图，就是我在研究出此算法的过程中引入的一个工具图。