POJ1084 Square Destroyer

Posted 2020-06-29 Bombe

1. 题目描述
由$n \times n, n \in [1, 5]$的正方形由$2 \times n \times (n+1)$根木棍组成，可能已经有些木棍被破坏，求至少还需破坏多少木根，可以使得不存在任何正方形？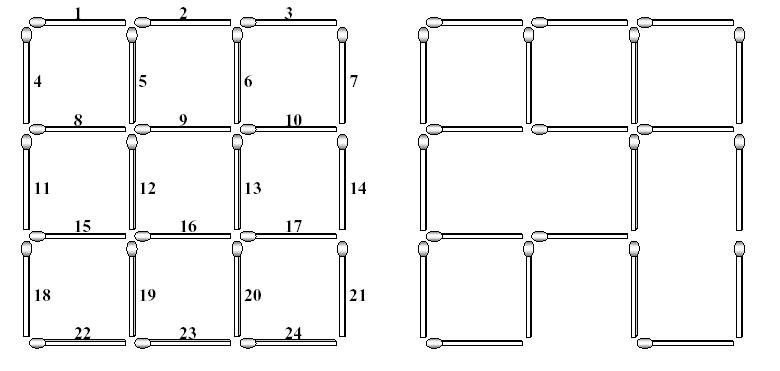

2. 基本思路
这是一道非常有趣的题目，可以使用IDA*解也可以用DLX解。可以试试5 0这组数据比较两者的性能差异。
(1) IDA*
使用IDA*处理，是因为最后的解的范围一定不是很大，因为数据很小。至多也就60根木棍。
首先可以预处理分别对正方形和木棍进行编号，进而预处理破坏每根木棍可以影响的正方形。
由于木棍和正方形都不超过60个，因此可以采用longlong进行状态压缩，一定要装压，否则就哭吧。
每次选择当前仍然存在的最小正方形，然后枚举它的每条边进行深搜。

(2) DLX
使用DLX解这道题很容易理解， 而且解5 0这组数据也很快。
首先仍然可以使用上述的预处理方法。从而可以得到当前木棍中仍然存在的正方形。
如果，当前不存在正方形则直接输出0。否则以正方形的个数初始化DLX。
接下来，枚举每条边，搜索它可以影响到的正方形，建立一个可行方案。
直接套用DLX可解，注意DLX加入H函数可以加速，而且效果还是挺明显的。

3. 代码
(1)IDA*

  1 /* 1084 */
  2 #include <iostream>
  3 #include <sstream>
  4 #include <string>
  5 #include <map>
  6 #include <queue>
  7 #include <set>
  8 #include <stack>
  9 #include <vector>
 10 #include <deque>
 11 #include <bitset>
 12 #include <algorithm>
 13 #include <cstdio>
 14 #include <cmath>
 15 #include <ctime>
 16 #include <cstring>
 17 #include <climits>
 18 #include <cctype>
 19 #include <cassert>
 20 #include <functional>
 21 #include <iterator>
 22 #include <iomanip>
 23 using namespace std;
 24 //#pragma comment(linker,"/STACK:102400000,1024000")
 25 
 26 #define sti                set<int>
 27 #define stpii            set<pair<int, int> >
 28 #define mpii            map<int,int>
 29 #define vi                vector<int>
 30 #define pii                pair<int,int>
 31 #define vpii            vector<pair<int,int> >
 32 #define rep(i, a, n)     for (int i=a;i<n;++i)
 33 #define per(i, a, n)     for (int i=n-1;i>=a;--i)
 34 #define clr                clear
 35 #define pb                 push_back
 36 #define mp                 make_pair
 37 #define fir                first
 38 #define sec                second
 39 #define all(x)             (x).begin(),(x).end()
 40 #define SZ(x)             ((int)(x).size())
 41 #define lson            l, mid, rt<<1
 42 #define rson            mid+1, r, rt<<1|1
 43 #define INF                0x3f3f3f3f
 44 #define mset(a, val)    memset(a, (val), sizeof(a))
 45 
 46 #define LL long long
 47 
 48 typedef struct {
 49     vector<LL> sq;
 50     int sz;
 51 } sqInfo_t;
 52 
 53 
 54 const int maxm = 65;
 55 int rowId[6][6];
 56 int colId[6][6];
 57 int n, tot;
 58 LL st;
 59 sqInfo_t sqInfo[6];
 60 
 61 void init_sq(int n) {
 62     int cnt = 0;
 63     sqInfo_t& info = sqInfo[n];
 64     vector<LL>& sq = info.sq;
 65     int& sz = info.sz;
 66     
 67     rep(i, 0, n) {
 68         rep(j, 0, n)
 69             rowId[i][j] = cnt++;
 70         rep(j, 0, n+1)
 71             colId[i][j] = cnt++;
 72     }
 73     rep(j, 0, n)
 74         rowId[n][j] = cnt++;
 75 
 76     cnt = 0;
 77     rep(i, 0, n) {
 78         rep(j, 0, n) {
 79             rep(k, 1, n+1) {
 80                 if (i+k>n || j+k>n)
 81                     break;
 82 
 83                 LL val = 0;
 84 
 85                 // Top
 86                 rep(l, 0, k) {
 87                     val |= (1LL << rowId[i][j+l]);
 88                 }
 89 
 90                 // Left
 91                 rep(l, 0, k) {
 92                     val |= (1LL << colId[i+l][j]);
 93                 }
 94 
 95                 // Down
 96                 rep(l, 0, k) {
 97                     val |= (1LL << rowId[i+k][j+l]);
 98                 }
 99 
100                 // Right
101                 rep(l, 0, k) {
102                     val |= (1LL << colId[i+l][j+k]);
103                 }
104                 
105                 sq.pb(val);
106                 ++sz;
107             }
108         }
109     }
110 }
111 
112 void init() {
113     rep(i, 1, 6)
114         init_sq(i);
115 }
116 
117 
118 bool dfs(int m, LL cst) {
119     const int& sz = sqInfo[n].sz;
120     const vector<LL>& sq = sqInfo[n].sq;
121     int h = 0;
122     LL st = -1, tmp = cst;
123     
124     rep(i, 0, sz) {
125         if ((tmp & sq[i]) == sq[i]) {
126             ++h;
127             tmp ^= sq[i];
128             if (st < 0)
129                 st = sq[i];
130         }
131     }
132     
133     if(h == 0)
134         return true;
135     
136     if (m < h)
137         return false;
138     
139     rep(i, 0, tot) {
140         if (st & (1LL << i)) {
141             if ( dfs(m-1, cst^(1LL<<i)) )    return true;
142         }
143     }
144     return false;
145 }
146 
147 void solve() {
148     int ans = -1;
149 
150     for (int i=0; i<=tot; ++i) {
151         if (dfs(i, st)) {
152             ans = i;
153             break;
154         }
155     }
156 
157     printf("%d\n", ans);
158 }
159 
160 int main() {
161     ios::sync_with_stdio(false);
162     #ifndef ONLINE_JUDGE
163         freopen("data.in", "r", stdin);
164         freopen("data.out", "w", stdout);
165     #endif
166 
167     int t;
168 
169     init();
170     scanf("%d", &t);
171     while (t--) {
172         scanf("%d", &n);
173         tot = n*(n+1)*2;
174         int k, x;
175         st = (1LL << tot) - 1;
176 
177         scanf("%d", &k);
178         while (k--) {
179             scanf("%d", &x);
180             --x;
181             st ^= (1LL << x);
182         }
183         solve();
184     }
185 
186     #ifndef ONLINE_JUDGE
187         printf("time = %d.\n", (int)clock());
188     #endif
189 
190     return 0;
191 }

(2)Dancing Links

  1 /* 1084 */
  2 #include <iostream>
  3 #include <sstream>
  4 #include <string>
  5 #include <map>
  6 #include <queue>
  7 #include <set>
  8 #include <stack>
  9 #include <vector>
 10 #include <deque>
 11 #include <bitset>
 12 #include <algorithm>
 13 #include <cstdio>
 14 #include <cmath>
 15 #include <ctime>
 16 #include <cstring>
 17 #include <climits>
 18 #include <cctype>
 19 #include <cassert>
 20 #include <functional>
 21 #include <iterator>
 22 #include <iomanip>
 23 using namespace std;
 24 //#pragma comment(linker,"/STACK:102400000,1024000")
 25 
 26 #define sti                set<int>
 27 #define stpii            set<pair<int, int> >
 28 #define mpii            map<int,int>
 29 #define vi                vector<int>
 30 #define pii                pair<int,int>
 31 #define vpii            vector<pair<int,int> >
 32 #define rep(i, a, n)     for (int i=a;i<n;++i)
 33 #define per(i, a, n)     for (int i=n-1;i>=a;--i)
 34 #define clr                clear
 35 #define pb                 push_back
 36 #define mp                 make_pair
 37 #define fir                first
 38 #define sec                second
 39 #define all(x)             (x).begin(),(x).end()
 40 #define SZ(x)             ((int)(x).size())
 41 #define lson            l, mid, rt<<1
 42 #define rson            mid+1, r, rt<<1|1
 43 #define INF                0x3f3f3f3f
 44 #define mset(a, val)    memset(a, (val), sizeof(a))
 45 
 46 #define LL __int64
 47 
 48 typedef struct {
 49     static const int maxr = 65;
 50     static const int maxc = 65;
 51     static const int maxn = maxr * maxc;
 52 
 53     int n, sz;
 54     int S[maxc];
 55     bool visit[maxc];
 56 
 57     int col[maxn];
 58     int L[maxn], R[maxn], U[maxn], D[maxn];
 59 
 60     int ansd;
 61 
 62     void init(int _n) {
 63         n = _n;
 64 
 65         rep(i, 0, n+1) {
 66             L[i] = i - 1;
 67             R[i] = i + 1;
 68             U[i] = i;
 69             D[i] = i;
 70             col[i] = i;
 71         }
 72 
 73         L[0] = n;
 74         R[n] = 0;
 75 
 76         sz = n + 1;
 77         memset(S, 0, sizeof(S));
 78         ansd = INF;
 79     }
 80 
 81     void addRow(const vi& columns) {
 82         int first = sz;
 83         int size = SZ(columns);
 84 
 85         rep(i, 0, size) {
 86             const int& c = columns[i];
 87 
 88             L[sz] = sz - 1;
 89             R[sz] = sz + 1;
 90 
 91             D[sz] = c;
 92             U[sz] = U[c];
 93             D[U[c]] = sz;
 94             U[c] = sz;
 95 
 96             col[sz] = c;
 97 
 98             ++S[c];
 99             ++sz;
100         }
101 
102         L[first] = sz - 1;
103         R[sz-1] = first;
104     }
105 
106     void remove_col(int c) {
107         for (int i=D[c]; i!=c; i=D[i]) {
108             L[R[i]] = L[i];
109             R[L[i]] = R[i];
110             --S[col[i]];
111         }
112     }
113 
114     void restore_col(int c) {
115         for (int i=D[c]; i!=c; i=D[i]) {
116             L[R[i]] = i;
117             R[L[i]] = i;
118             ++S[col[i]];
119         }
120     }
121 
122     int H() {
123         int ret = 0;
124 
125         memset(visit, false, sizeof(visit));
126         for (int i=R[0]; i; i=R[i]) {
127             if (visit[col[i]])
128                 continue;
129 
130             ++ret;
131             visit[col[i]] = true;
132             for (int j=D[i]; j!=i; j=D[j]) {
133                 for (int k=R[j]; k!=j; k=R[k]) {
134                     visit[col[k]] = true;
135                 }
136             }
137         }
138 
139         return ret;
140     }
141 
142     void dfs(int d) {
143         int delta = H();
144 
145         if (d+delta >= ansd)
146             return ;
147 
148         if (R[0] == 0) {
149             ansd = d;
150             return ;
151         }
152 
153         int c = R[0];
154         for (int i=R[0]; i; i=R[i]) {
155             if (S[i] < S[c])
156                 c = i;
157         }
158 
159         for (int i=D[c]; i!=c; i=D[i]) {
160             remove_col(i);
161             for (int j=R[i]; j!=i; j=R[j]) {
162                 remove_col(j);
163             }
164             dfs(d + 1);
165             for (int j=L[i]; j!=i; j=L[j]) {
166                 restore_col(j);
167             }
168             restore_col(i);
169         }
170     }
171 
172 } DLX;
173 
174 typedef struct {
175     vector<LL> sq;
176     int sz;
177 } sqInfo_t;
178 
179 DLX solver;
180 const int maxm = 65;
181 bool mark[maxm];
182 int valid[maxm];
183 int rowId[6][6];
184 int colId[6][6];
185 int n, tot;
186 LL st;
187 sqInfo_t sqInfo[6];
188 
189 void init_sq(int n) {
190     int cnt = 0;
191     sqInfo_t& info = sqInfo[n];
192     vector<LL>& sq = info.sq;
193     int& sz = info.sz;
194 
195     rep(i, 0, n) {
196         rep(j, 0, n)
197             rowId[i][j] = cnt++;
198         rep(j, 0, n+1)
199             colId[i][j] = cnt++;
200     }
201     rep(j, 0, n)
202         rowId[n][j] = cnt++;
203 
204     cnt = 0;
205     rep(i, 0, n) {
206         rep(j, 0, n) {
207             rep(k, 1, n+1) {
208                 if (i+k>n || j+k>n)
209                     break;
210 
211                 LL val = 0;
212 
213                 // Top
214                 rep(l, 0, k) {
215                     val |= (1LL << rowId[i][j+l]);
216                 }
217 
218                 // Left
219                 rep(l, 0, k) {
220                     val |= (1LL << colId[i+l][j]);
221                 }
222 
223                 // Down
224                 rep(l, 0, k) {
225                     val |= (1LL << rowId[i+k][j+l]);
226                 }
227 
228                 // Right
229                 rep(l, 0, k) {
230                     val |= (1LL << colId[i+l][j+k]);
231                 }
232 
233                 sq.pb(val);
234                 ++sz;
235             }
236         }
237     }
238 }
239 
240 void init() {
241     rep(i, 1, 6)
242         init_sq(i);
243 }
244 
245 void solve() {
246     const vector<LL>& sq = sqInfo[n].sq;
247     const int& sz = sqInfo[n].sz;
248     int m = 0;
249 
250     rep(i, 0, sz) {
251         if ((st & sq[i]) == sq[i]) {
252             valid[m++] = i;
253         }
254     }
255 
256     if (m == 0) {
257         puts("0");
258         return ;
259     }
260 
261     solver.init(m);
262 
263     rep(i, 0, tot) {
264         if (mark[i]) {
265             vi vc;
266 
267             rep(j, 0, m) {
268                 if (sq[valid[j]] & (1LL << i))
269                     vc.pb(j+1);
270             }
271 
272             if (SZ(vc) > 0) {
273                 solver.addRow(vc);
274             }
275         }
276     }
277 
278     solver.dfs(0);
279     int ans = solver.ansd;
280 
281     printf("%d\n", ans);
282 }
283 
284 int main() {
285     ios::sync_with_stdio(false);
286     #ifndef ONLINE_JUDGE
287         freopen("data.in", "r", stdin);
288         freopen("data.out", "w", stdout);
289     #endif
290 
291     int t;
292 
293     init();
294     scanf("%d", &t);
295     while (t--) {
296         scanf("%d", &n);
297         memset(mark, true, sizeof(mark));
298         tot = n*(n+1)*2;
299         int k, x;
300         st = (1LL << tot) - 1;
301 
302         scanf("%d", &k);
303         while (k--) {
304             scanf("%d", &x);
305             mark[--x] = false;
306             st ^= (1LL << x);
307         }
308         solve();
309     }
310 
311     #ifndef ONLINE_JUDGE
312         printf("time = %d.\n", (int)clock());
313     #endif
314 
315     return 0;
316 }

4. 数据生成器

 1 import sys
 2 import string
 3 from random import randint, shuffle
 4 
 5     
 6 def GenData(fileName):
 7     with open(fileName, "w") as fout:
 8         t = 20
 9         fout.write("%d\n" % (t))
10         for tt in xrange(t):
11             n = randint(1, 5)
12             tot = n * (n + 1)
13             taken = randint(1, tot)
14             L = range(1, tot+1)
15             shuffle(L)
16             fout.write("%d %d\n" % (n, taken))
17             fout.write(" ".join(map(str, L[:taken])) + "\n")
18             
19             
20 def MovData(srcFileName, desFileName):
21     with open(srcFileName, "r") as fin:
22         lines = fin.readlines()
23     with open(desFileName, "w") as fout:
24         fout.write("".join(lines))
25 
26         
27 def CompData():
28     print "comp"
29     srcFileName = "F:\Qt_prj\hdoj\data.out"
30     desFileName = "F:\workspace\cpp_hdoj\data.out"
31     srcLines = []
32     desLines = []
33     with open(srcFileName, "r") as fin:
34         srcLines = fin.readlines()
35     with open(desFileName, "r") as fin:
36         desLines = fin.readlines()
37     n = min(len(srcLines), len(desLines))-1
38     for i i