P1133 教主的花园

Posted 2020-10-04 范仁义

P1133 教主的花园

题目描述

教主有着一个环形的花园，他想在花园周围均匀地种上n棵树，但是教主花园的土壤很特别，每个位置适合种的树都不一样，一些树可能会因为不适合这个位置的土壤而损失观赏价值。

教主最喜欢3种树，这3种树的高度分别为10，20，30。教主希望这一圈树种得有层次感，所以任何一个位置的树要比它相邻的两棵树的高度都高或者都低，并且在此条件下，教主想要你设计出一套方案，使得观赏价值之和最高。

输入输出格式

输入格式：

 

输入文件garden.in的第1行为一个正整数n，表示需要种的树的棵树。

接下来n行，每行3个不超过10000的正整数ai，bi，ci，按顺时针顺序表示了第i个位置种高度为10，20，30的树能获得的观赏价值。

第i个位置的树与第i+1个位置的树相邻，特别地，第1个位置的树与第n个位置的树相邻。

 

输出格式：

 

输出文件garden.out仅包括一个正整数，为最大的观赏价值和。

 

输入输出样例

输入样例#1：

4 
1 3 2 
3 1 2 
3 1 2 
3 1 2

输出样例#1：

11

说明

【样例说明】

第1～n个位置分别种上高度为20，10，30，10的树，价值最高。

【数据规模与约定】

对于20%的数据，有n≤10；

对于40%的数据，有n≤100；

对于60%的数据，有n≤1000；

对于100%的数据，有4≤n≤100000，并保证n一定为偶数。

 

 

分析：

把F[i][j][k]定义为第i个节点高度为j，k=0表示前面比他小； k=1表示前面比他大； 

但是这样我们第一位要靠第n位来更新； 
那我们直接不更新第一位； 

从第二位来，然后跑完后把n位和1位结合一下就好了；

这是一个环，从哪个位置进去都是一样。因为我们1号节点需要n来更新，所以我们就直接从2号节点开始。

 

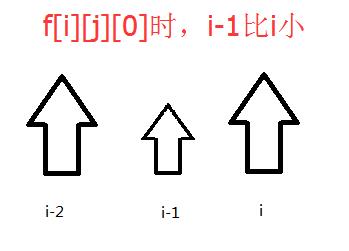
故f[i][j][0]=max(f[i][j][0],f[i-1][k][1]+a[i][j]);

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int f[100005][4][2],a[100005][4];
 4 int ans,n;
 5 int main()
 6 {
 7     //读入数据 
 8     scanf("%d",&n);
 9     for(int i=1;i<=n;i++)
10         for(int j=1;j<=3;j++)
11             scanf("%d",&a[i][j]);
12     //从2开始更新，先不管第一个 
13     for(int i=2;i<=n;i++)
14         for(int j=1;j<=3;j++){//三种树 ，j表示第i棵树的长度 
15             for(int k=1;k<=3;k++)//三种树, k表示它前面那棵树的长度 
16                 //前面的树（第i-1棵）比较短的情况，那么第i-2棵树要比i-1棵树高，f[i-1][k][1] ，1表示前面的树比它高 
17                 if(j>k)f[i][j][0]=max(f[i][j][0],f[i-1][k][1]+a[i][j]);else
18                 if(j<k)f[i][j][1]=max(f[i][j][1],f[i-1][k][0]+a[i][j]);
19             }
20     // 更新第一颗树       
21     for(int j=1;j<=3;j++)
22         for(int k=1;k<=3;k++)
23             if(j>k)ans=max(ans,a[1][j]+f[n][k][1]);else
24             if(j<k)ans=max(ans,a[1][j]+f[n][k][0]);
25     printf("%d",ans);
26 }