多项式艺术：浅谈FFT和NTT算法（未完待续）

Posted 2020-10-04

　　什么是多项式？

　　百度百科说：“由若干个单项式相加组成的代数式叫做多项式。多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数。”

　　也就是说，形如的式子，就叫做多项式。这样的式子，也能写作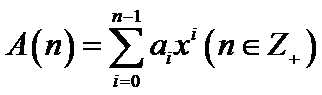。很显然，多项式加上（或是减上）多项式也是多项式，复杂度是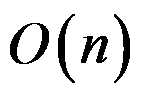的。但是，如果多项式想要乘上一个多项式，那么也可以，最简单的方法却是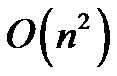的。

　　不过，FFT算法会告诉你，就够了。

多项式乘法

　　我们说的，多项式想要乘上一个多项式，那就是多项式乘法，人称“卷积”。我们方才所看到的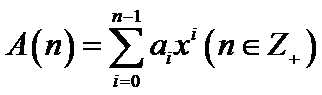，被称为多项式的“系数表示法”（一个多项式是由其次数与系数确定的）。对于一个n项的多项式，如果把每个系数都看成一个未知数，那么该多项式就也能看做一个n元一次方程。事实告诉我们，如果有n个n元一次方程（而且这n个方程不存在等比放缩），那么就能唯一确定这n个系数（高斯消元就是这么干的）。

　　于是，“点值表示法”横空出世。对于一个n项的多项式，可以由n个确定的x_i与其取值y_i=A(x_i)唯一确定，而这样的表示是一个“点-值”对的序列{(x₀,y₀),(x₁,y₁),....,(x_n-1,y_n-1)}。每一个多项式可以有多种（其实是无穷种）点值表示法，但只有一种系数表示法。而无论是点值表示法还是系数表示法，n确定了，那么这个多项式就唯一确定了。

　　多项式乘法，就是有两个多项式A和B，现在要算出C=A*B。我们平时用惯了系数表示法，却不习惯点值表示法。但是偏偏，点值表示法用来算乘法就很简单。因为，算出的这样的一个多项式C，对于任意的x，一定满足C(x)=A(x)*B(x)。也就是说：

　　假设A的点值表达式为{(x₀,y₀),(x₁,y₁),....,(x_n-1,y_n-1)}

　　而B的点值表达式为{(x₀,y‘₀),(x₁,y‘₁),....,(x_n-1,y‘_n-1)}

　　那么C的点值表达式为{(x₀,y₀y‘₀),(x₁,y₁y‘₁),....,(x_n-1,y_n-1y‘_n-1)}

FFT的策略

　　FFT在此崭露了头角。现在，我们读入了两个多项式A和B（如果A有n次而B有m次则C有n+m-1次），我们可以算出A与B的点值表示法，然后算出C的点值表示法，然后回带算出C的各项系数。这样三步，分别称作：求值、点值乘法、插值（在该插系数的地方插入正确的值）。

　　点值乘法是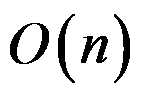的，而FFT要在的时间内求出A、B的点值表示法，要在的时间内回带算出C的各项系数。

　　FFT证明，可以做到这一要求。如果无法满足，那么要求出A的点值表示法就难免是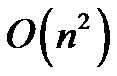的，因为有n个x，每一个x又有n项系数要去乘。看上去，似乎是不可能的。确实，如果随便求出一种点值表示法确实不优，但是x我们可以选择。

　　FFT选择了复数单位根。

复数与单位根

　　在历史上，复数的引入是与求三次方程x³=px+q根的解析公式相联系的。

　　十六世纪的最初三十年间，意大利数学家塔尔塔利亚曾经证明了该方程的根总可以表示为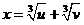，其中u和v是方程组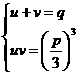的解。

　　例如，若求三次方程x³=9x+28的根，可对该方程作出上述方程组，并求得两组解：u=27，

v=1和u=1，v=27。然后，便可解得x=4。

　　但是，存在一些三次方程，使上述那个关于u、v的方程组无实数解，但那个三次方程却显然有实数解。例如，方程x³=15x+4就是一个悲剧的例子。　

　　意大利数学家邦别里在1572年首先解释了这个当时不清楚的现象，实质上，他的解释根据是以引进复数的概念和复数的运算法则为基础的。但是十九世纪之前，许多数学家对复数本身的存在仍持怀疑的态度。直到十九世纪，高斯发表了著作，对复数作了直观的几何描述（把复数作为平面上的点或者向量）。

　　构成复数集的方法之一，是把新的数即方程x²+1=0的根并入实数集而将实数集扩充。而由条件i²=-1确定的记号i称为虚数单位。通常，复数a+bi用一个字母z表示：z=a+bi。a称为z的实部（Re z），b称为z的虚部（Im z）。

　　为了直观的理解虚数，我们可以使用平面直角坐标系，正如理解实数可以使用数轴一样。数轴上的每一个点x都与一个实数x一一对应，而坐标系中的每一个点(x,y)都与一个虚数x+yi对应。