机器学习之正则化

Posted 2020-10-04 steed

前言

           以下内容是个人学习之后的感悟，转载请注明出处~

 

 

 

过拟合

         过拟合是一种现象。当我们提高在训练数据上的表现时，在测试数据上反而下降，这就被称为过拟合，或过配。过拟合发生

的本质原因，是由于监督学习问题的不适定：在高中数学我们知道，从n个（线性无关）方程可以解n个变量，解n+1个变量就会解

不出。在监督学习中，当样本数远远少于特征数时，会发生过拟合现象。

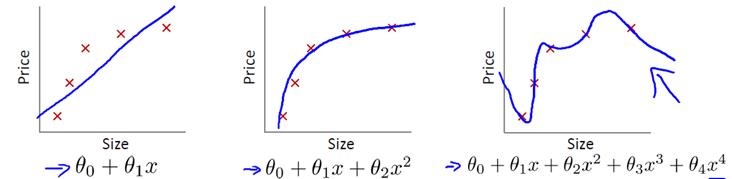
         为了更直观地了解过拟合，请观察下面的图片。可以看到，左边是欠拟合，中间是正好拟合，右边是过拟合。经过对比，可以

看出过拟合能够符合所有的训练样本，但是结构弯弯曲曲，无法准确地测试数据。

                  

            针对过拟合现象一般有两个处理方法：

           1、尽量减少特征量，将一些冗余的、信息量少的特征量舍弃。

           2、使用正则化

 

L2正则化

1、原理

       使用正则化，其实只需要在代价函数后面加一个惩罚项即可。

       Why? 为什么加一个惩罚项就可以了？

        是的，看下面的例子。我们可以看到，二次多项式已经可以实现正确的拟合，采用四次多项式，就会产生过拟合。此时，我们

在代价函数的后面加上1000*（θ₃²，θ₄²）项，当代价函数最小化的时候，θ₃≈0，θ₄≈0，即假设函数变换到了二次多项式，避免了

过拟合。

                       

          如果我们像惩罚 θ₃ 和 θ₄ 这样惩罚其它参数，那么我们往往可以得到一个相对较为简单的假设函数。实际上，这些参数的值

越小，通常对应于越光滑的函数，也就是更加简单的函数。因此 就不易发生过拟合的问题。按照惯例，我们没有去惩罚 θ₀，因此

θ₀ 的值是大的。

 

2、线性回归正则化

•  梯度下降法：

                                因为 始终为正，因此 一般来说其值比1小一点点。

                                   

•   正规方程法：

                               

 

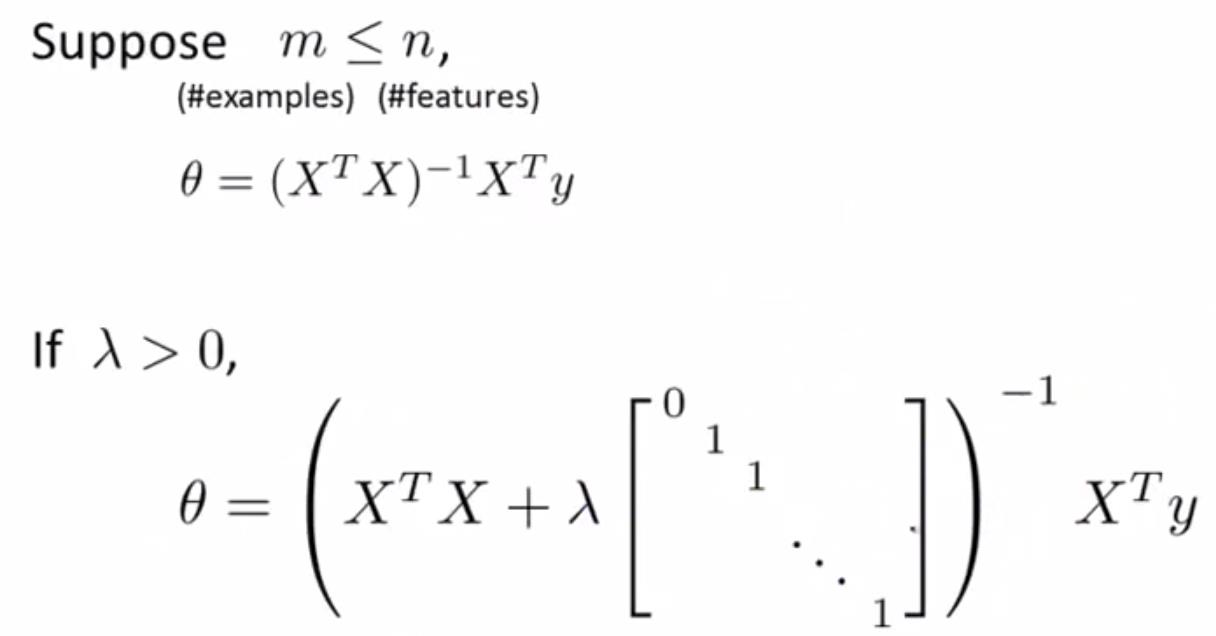
3、逻辑回归正则化

                              

注1：λ的选取起到很关键的作用，之后在机器学习之模型选择与改进的模型优化模块中会讲到如何实现为λ取值。

注2：正则化不仅能够解决过拟现象，还能解决正规方程中奇异矩阵的问题。

注3：一般使用L2正则化，只是计算量较大。

 

Dropout随机失活正则化

　　Dropout随机失活正则化，顾名思义，就是把一些神经单元随机失活，下一次有可能又会被重新激活。

                             

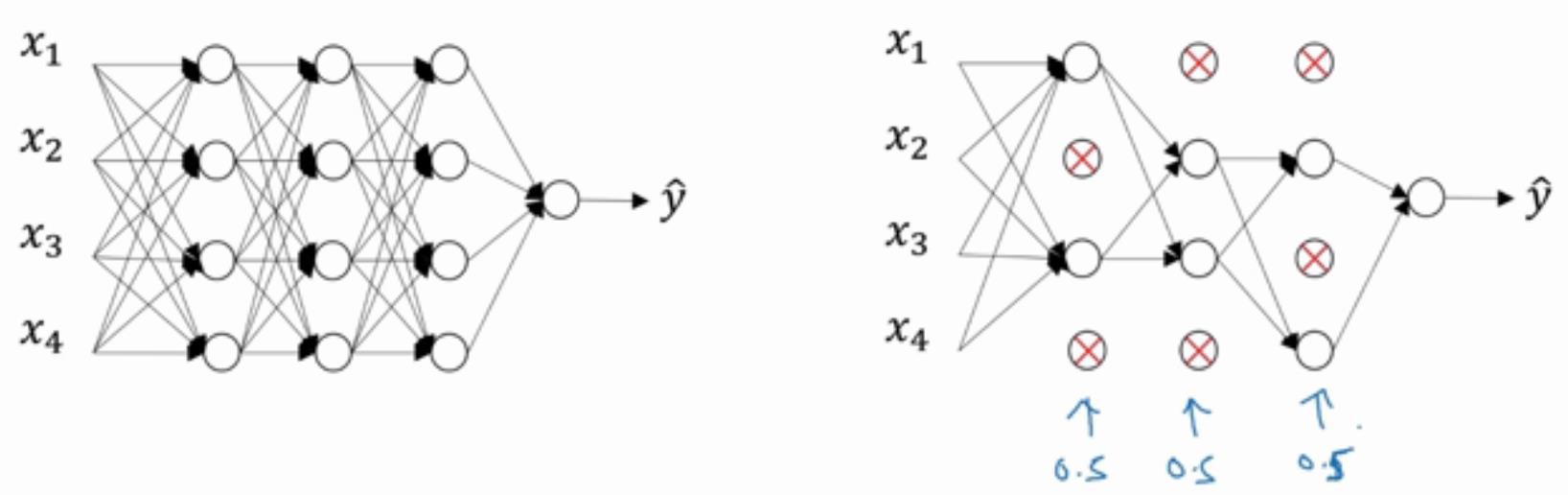
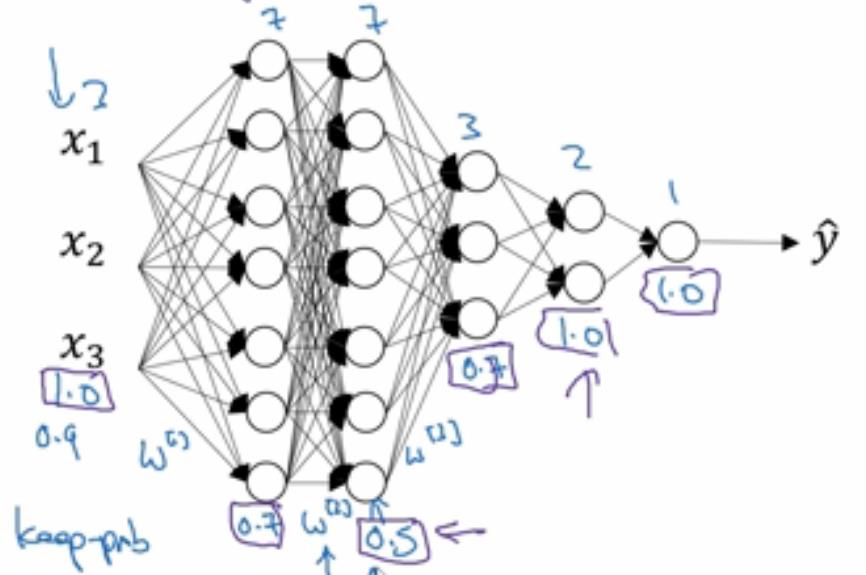
 　　其与L2正则化有所不同，L2正则化对不同权重的衰减是不同的，它取决于倍增的激活函数的大小。而Dropout随机失活正则

化，是对每层神经网络取一随机失活概率（其取值可根据该层神经单元的数目，如下图）。可以看得出，随机失活正则化在神经网

络这一方面可能用的较多。

                                                               

 

 

Data augmentation数据扩增

　　数据扩增，可以通过改变数据的方法来扩增数据，其达到的效果与正则化相似。

                                      

 

 

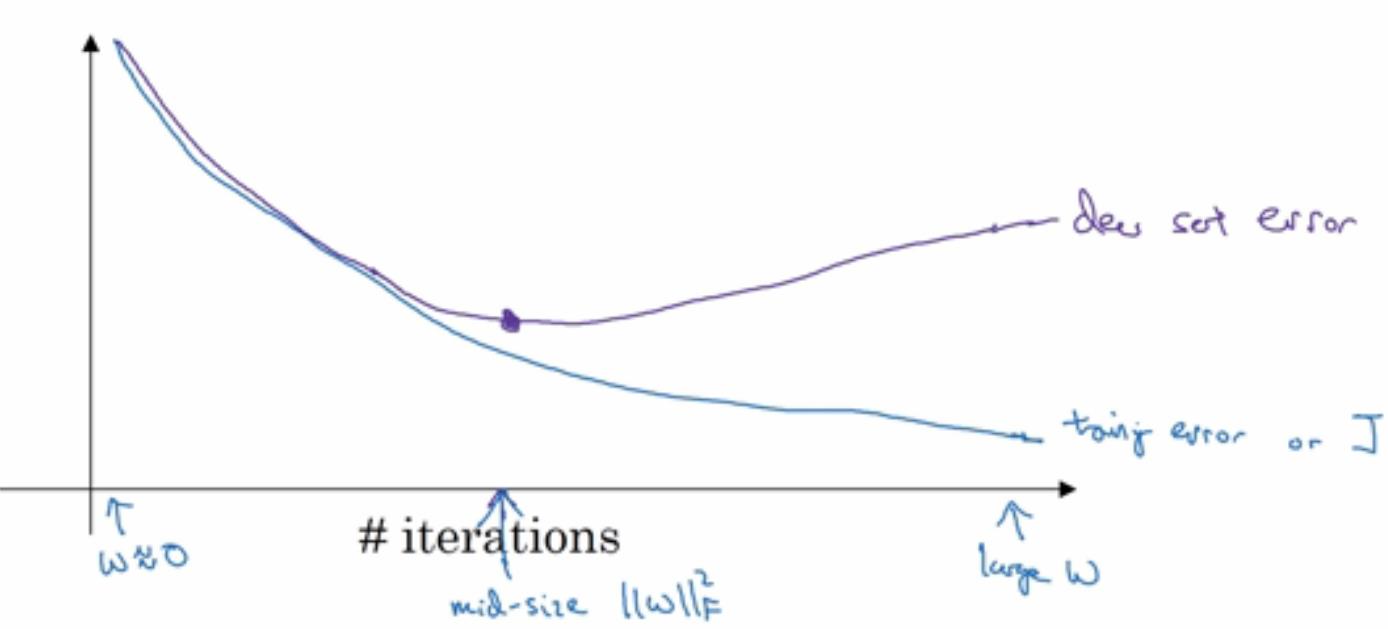
Early stopping

　　从下图可以看出，当迭代不断进行时，训练误差以及校验误差的趋势。当迭代到一定值时，校验误差是较小的，此时停止迭代，

就可达到正则化相似的效果。

                                             

 

 

 

 

以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~