使用索贝尔(Sobel)进行梯度运算时的数学意义和代码实现研究

Posted 2020-10-04 GreenOpen专注图像处理

对于做图像处理的工程师来说，Sobel非常熟悉且常用。但是当我们需要使用Sobel进行梯度运算，且希望得到“数学结果”（作为下一步运算的基础）而不是“图片效果”的时候，就必须深入了解Sobel的知识原理和OpenCV实现的细节（当然我们是OpenCV支持则）。这里对具体内容进行研究。

对于做图像处理的工程师来说，Sobel非常熟悉且常用。但是当我们需要使用Sobel进行梯度运算，且希望得到“数学结果”（作为下一步运算的基础）而不是“图片效果”的时候，就必须深入了解Sobel的知识原理和OpenCV实现的细节（当然我们是OpenCV支持则）。这里对具体内容进行研究。

一、基本原理

一般来说，用来表示微分的最常用的算子是索贝尔(Sobel)算子，它可以实现任意阶导数和混合偏导数(例如: ∂²/∂x∂y)。

在x方向上用Sobel算子进行近似一阶求导的结果

Sobel算子效果，y方向近似一阶导数

OpenCV中给出了函数使用的定义

void cv::Sobel(
  cv::InputArray  src,                 // 源图像
  cv::OutputArray dst,                 // 目标图像
  int             ddepth,              // 像素深度 (如CV_8U)
  int             xorder,              // x方向对应的倒数顺序
  int             yorder,              // y方向对应的倒数顺序
  cv::Size        ksize      = 3,      // 核大小
  double          scale      = 1,      // 阈值
  double          delta      = 0,      // 偏移
  int             borderType = cv::BORDER_DEFAULT  // 边框外推方法
);

1、其中src和dst是源图像和目标图像，可以通过指明参数ddepth来确定目标图像的深度或类型（如CV_32F）。举个例子，如果src是一幅8位图像，那么dst需要至少CV_16S的深度保证不出现溢出；

2、xorder和yorder是求导顺序，其取值范围为0、1和2。0表示在这个方向上不进行求导，那2代表什么？

3、ksize是一个奇数，表示了调用的滤波器的宽和高，目前最大支持到31；

4、阈值和偏移将在把结果存入dst前调用，这有助于你将求导结果可视化.borderType参数的功能与其他卷积操作完全一样。

上面有一个遗留问题，就是xorder(yorder)取2的时候代表什么？为此翻阅OpenCV源码

step1

 

 

step 2

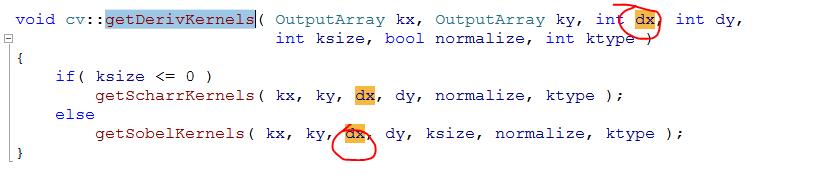
step3

 

static void getSobelKernels( OutputArray _kx, OutputArray _ky,
                             int dx, int dy, int _ksize, bool normalize, int ktype )
{
    int i, j, ksizeX = _ksize, ksizeY = _ksize;
    if( ksizeX == 1 && dx > 0 )
        ksizeX = 3;
    if( ksizeY == 1 && dy > 0 )
        ksizeY = 3;
    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    _kx.create(ksizeX, 1, ktype, -1, true);
    _ky.create(ksizeY, 1, ktype, -1, true);
    Mat kx = _kx.getMat();
    Mat ky = _ky.getMat();
    if( _ksize % 2 == 0 || _ksize > 31 )
        CV_Error( CV_StsOutOfRange, "The kernel size must be odd and not larger than 31" );
    std::vector<int> kerI(std::max(ksizeX, ksizeY) + 1);
    CV_Assert( dx >= 0 && dy >= 0 && dx+dy > 0 );
    for( int k = 0; k < 2; k++ )
    {
        Mat* kernel = k == 0 ? &kx : &ky;
        int order = k == 0 ? dx : dy;
        int ksize = k == 0 ? ksizeX : ksizeY;
        CV_Assert( ksize > order );
        if( ksize == 1 )
            kerI[0] = 1;
        else if( ksize == 3 )
        {
            if( order == 0 )
                kerI[0] = 1, kerI[1] = 2, kerI[2] = 1;
            else if( order == 1 )
                kerI[0] = -1, kerI[1] = 0, kerI[2] = 1;
            else
                kerI[0] = 1, kerI[1] = -2, kerI[2] = 1;
        }
        else
        {
            int oldval, newval;
            kerI[0] = 1;
            for( i = 0; i < ksize; i++ )
                kerI[i+1] = 0;
            for( i = 0; i < ksize - order - 1; i++ )
            {
                oldval = kerI[0];
                for( j = 1; j <= ksize; j++ )
                {
                    newval = kerI[j]+kerI[j-1];
                    kerI[j-1] = oldval;
                    oldval = newval;
                }
            }
            for( i = 0; i < order; i++ )
            {
                oldval = -kerI[0];
                for( j = 1; j <= ksize; j++ )
                {
                    newval = kerI[j-1] - kerI[j];
                    kerI[j-1] = oldval;
                    oldval = newval;
                }
            }
        }
        Mat temp(kernel->rows, kernel->cols, CV_32S, &kerI[0]);
        double scale = !normalize ? 1. : 1./(1 << (ksize-order-1Canny边缘检测算法

Sobel边缘检测算法（转载）

使用cv2.Sobel()cv2.Scharr()cv2.Laplacian()寻找图像的梯度边缘

图像分析：边缘检测中的梯度算子

《OpenCV:Sobel算子理论与OpenCV代码实现》

opencv用sobel算子进行处理后的图像，怎么提取梯度信息？