Geomystery(几何迷城)的游戏引擎设计与实现
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Geomystery(几何迷城)的游戏引擎设计与实现相关的知识,希望对你有一定的参考价值。
在这里介绍Geomystery(几何迷城)的游戏引擎设计与实现。
业务逻辑:
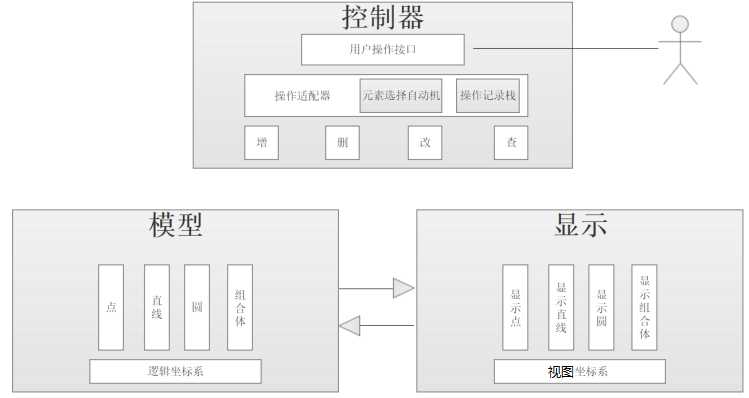
引擎采用模块化的MVC(Model模型,View视图,Controller控制)设计方式,这样有助于运用多种设计模式,便于日后的修改与维护。
引擎采用模块化的MVC(Model模型,View视图,Controller控制)设计方式,这样有助于运用多种设计模式,便于日后的修改与维护。
M模型坐标系中的模型是被操作的对象,模型坐标系是被“显示坐标系”显示的单位。
V视图(显示坐标系)是模型在用户屏幕的一个投影,这也和显卡、显示器的工作原理有关。
C控制器操作某个逻辑坐标系模型A,或者每次操作后由控制器直接通知视图(显示坐标系)刷新模型A的投影a,或者由“监听器”(监听者模式)发现模型A被“更新(改变)”,之后通知视图(显示坐标系)刷新a。
显卡和显示器:
WIN2D封装了DirectX,在屏幕上一个区域(DC)显示一些静态内容,或者每隔一段时间(一般是1/60s,即60fps)在屏幕上的一个区域刷新显示一些内容。所以每次刷新,只需要遍历V视图(显示坐标系),把其中的内容呈现给用户,这样用户画线时的动态过程就可以被看到,同时用户改变程序窗口大小(刷新显示区DC)的操作也不会清空屏幕。
“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。”庐山只有一座,而在同一时刻,不同的人看庐山,能看到不同的庐山。所以对于一个“逻辑的”坐标系M,可能对应多个“显示的”坐标系V1V2V3V4,每个显示坐标系Vn都有自己的“操纵杆”Cn与控制器相连,他们都可以通过自己的操纵杆Cx操作自己看到的(其实是同一个)逻辑坐标系。于是,如果多个用户同时操作,就可能有冲突,需要使用操作系统学到的同步互斥方法,由于这次生产实习时间有限,所以这里简化一下,只有一个控制器,有一个主“屏幕”(视图显示坐标系),其他屏幕都是副屏幕,只能观察,没有操作功能。一个娃娃机有前后左右四块玻璃观察窗,但是只有一套操纵杆。
| M | 逻辑坐标系,系统坐标系 |
| V | 显示坐标系,视图坐标系,用户坐标系,用户屏幕 |
| C | 用户控制器,操纵杆 |

逻辑坐标系中的元素:
0,几何元素Geometry。几何元素有一个坐标系内唯一的编号(id),记录了自己的投影(们),记录了自己受谁影响rely,记录了自己影响谁influence。
几何元素分为点Point和点集合PointSet。
1,点就是一个逻辑点,关键属性是逻辑坐标XY。
2,点集是一个接口(interface),因为这款游戏是尺规作图,所以点集只分线(Line)和圆(Circle)
(为什么是Circle而不是Ellipse,因为圆规只能画圆,这里涉及到圆的定义方式,所以只提供圆工具,椭圆工具可以后续添加)
点集接口有一个交点List<Point2> IPointSet.Intersection(IPointSet another)函数需要后续实现
3,线分为线段射线直线,所以我们需要一个LineType来记录线的线型

1 public enum LineType 2 { 3 // 4 // 摘要: 5 // 直线 6 Straight = 0, 7 // 8 // 摘要: 9 // 射线 10 Ray = 1, 11 // 12 // 摘要: 13 // 线段 14 Line = 2 15 }
但是两点的定义方式并不够,(p1是第一个点,p2是第二个点),如果用户是过线(含延长线)和一点做的垂线,这个逻辑也需要体现,
所以我们需要一个LineRely来记录线的构造(生成)方式

1 public enum LineRely 2 { 3 // 4 // 摘要: 5 // 常规方式,p1,p2两点确定一条直线 6 Normal = 0, 7 // 8 // 摘要: 9 // 垂线,依赖列表的一条线加上线上或者线外点p1,过p1作依赖点的垂线 10 Perpendicular = 1, 11 // 12 // 摘要: 13 // 垂直平分线,p1,p2两点连线的中垂线 14 PerpendicularBisector = 2, 15 // 16 // 摘要: 17 // 垂直平分线,p1,p2两点连线的中垂线 18 AngleBisector = 3, 19 }
与构造方式LineRely配套的需要一些属性(字段),比如垂线构造(三个点,一点一线),中垂线构造(两个点,一个线段),角平分线构造(三个点,两条射线)等方式
4,圆的构造就容易很多
两个点,一个是圆心,另一个是圆上的一点
(为什么不用半径,因为用户依靠鼠标的点击生成圆周上的点,而且这个点是圆的重要的控制点,所以后续半径需要计算生成)
视图坐标系中的元素:
一条逻辑线在一个坐标系中有几个像?是一个吗?不是。
在这个引擎中,视图坐标系中的元素是可以直接显示的,如果你画的线是一个线段(或者是一条射线),一条逻辑线就会有两个视图线,一条实线,一条虚线,先画虚线(延长线),在画实线。
视图坐标系中的元素都是几何体吗?不是。(注释和标签,待实现)
视图坐标系中可以放置OutputText

1 /// <summary> 2 /// 屏幕上的提示文本,或者是屏幕上元素的“名字标签” 3 /// </summary> 4 public class OutputText : ICanOutput 5 { 6 /// <summary> 7 /// 文本内容 8 /// </summary> 9 public string text { get; set; } 10 11 /// <summary> 12 /// 在屏幕上的窗体(canva)中,这个文本“写”在哪里 13 /// </summary> 14 public Vector2 viewPoint { get; set; } 15 16 /// <summary> 17 /// 文字颜色 18 /// </summary> 19 public Color fontColor { get; set; } 20 21 /// <summary> 22 /// 文字格式 23 /// </summary> 24 public CanvasTextFormat format { get; set; } 25 26 /// <summary> 27 /// 这个文字是否是某个几何体的标签(名字) 28 /// </summary> 29 public Models.Geometry.Geometry rely { get; set; } 30 }
文本没有”原像”(借用数学中函数的概念),但是有依赖,比如这个文本是一个点的标签,依赖保证了文本的坐标始终围绕在这个点一定范围周边,不能被拖动太远
两个方向的映射:逻辑到显示,显示到逻辑。
M逻辑坐标系是一张无限大的白纸
V视图坐标系是白纸上的一个矩形框,V中有两个关键的属性,向量vector,单位长度unitlength,
v是这样一个向量,由逻辑坐标系指向视图(现实)坐标系的“中心”
ul是逻辑坐标系的1单位长度相当于多少 DIP(DIP代表“器件独立像素”。这是可以与物理像素相同,大于或小于的虚拟化单元。)
映射有两种方式,
“左上角投影”:视图(现实)坐标系的“中心”在“屏幕”左上角,不关心屏幕的长宽

1 // <summary> 2 /// 逻辑坐标系到屏幕显示坐标系的转换(左上角模式) 3 /// </summary> 4 /// <param name="p2"></param> 5 /// <returns>v2</returns> 6 public Vector2 ToVector2Upper_Left_Corner(Point2 p2) 7 { 8 float x = p2.X - vector.X; 9 float y = p2.Y - vector.Y; 10 x = x / unitLength; 11 y = -y / unitLength; 12 Vector2 v2 = new Vector2(x,y); 13 return v2; 14 } 15 /// <summary> 16 /// 屏幕显示坐标系到逻辑坐标的转换(左上角模式) 17 /// </summary> 18 /// <param name="v2"></param> 19 /// <returns>Point2 p2</returns> 20 public Point2 ToPoint2Upper_Left_Corner(Vector2 v2) 21 { 22 Point2 p2 = new Point2() { X = (v2.X*unitLength+vector.X), Y = -(v2.Y*unitLength+vector.Y) }; 23 return p2; 24 }
“中心投影”:视图(现实)坐标系的“中心”在“屏幕”中心,需要知道屏幕的长和宽,然后减半

1 /// <summary> 2 /// 逻辑坐标系到屏幕显示坐标系的转换(中心模式) 3 /// </summary> 4 /// <param name="p2"></param> 5 /// <returns>屏幕上的点</returns> 6 public Vector2 ToVector2(Point2 p2) 7 { 8 Vector2 vop = new Vector2() { X = p2.X - vector.X, Y = vector.Y - p2.Y }; 9 //if (WindowHeight <= 0 || WindowWidth <= 0) throw new Exception("中心构造方式需要了解canvas画布的actual宽和高"); 10 Vector2 half = new Vector2() { X = WindowWidth / 2, Y = WindowHeight / 2 }; 11 Vector2 result = half + vop * unitLength; 12 return result; 13 } 14 /// <summary> 15 /// 屏幕显示坐标系到逻辑坐标的转换(中心模式) 16 /// </summary> 17 /// <param name="v2"></param> 18 /// <returns>逻辑坐标系中的点</returns> 19 public Point2 ToPoint2(Vector2 v2) 20 { 21 if (WindowHeight <= 0 || WindowWidth <= 0) throw new Exception("中心构造方式需要了解canvas画布的actual宽和高"); 22 Vector2 half = new Vector2() { X = WindowWidth / 2, Y = WindowHeight / 2 }; 23 Vector2 vop = (v2 - half) / unitLength; 24 Point2 p2 = new Point2() { X = (vop.X + vector.X), Y = -vop.Y + vector.Y }; 25 return p2; 26 }
四种操作,“增删改查”:用户可能对一个几何体有定义(创建),移动,变形,删除等操作,这些操作都会被记录在操作栈中,这样用户可以撤销重做。查询操作主要包含在代码逻辑中,也是必不可少的。
“繁琐”的“绑定”:对于一个引擎的每一个“零件”,都应该记录丰富的信息,这种丰富可能是繁琐多余的,但是会给操作带来方便。
逻辑坐标系知道有多少用户在看自己(逻辑坐标系绑定显示坐标系(们)),显示坐标系知道自己看的是谁(显示坐标系绑定逻辑坐标系),逻辑坐标系知道自己里面有多少逻辑几何元素,每个逻辑几何元素知道自己在哪个逻辑坐标系中,视图坐标系知道自己里面有多少视图几何元素或其他,每个视图几何元素知道自己位于哪个视图坐标系中,每个逻辑几何元素知道自己有多少个视图几何元素,每个视图几何元素知道自己是哪个逻辑几何元素的“投影像”。
以上是关于Geomystery(几何迷城)的游戏引擎设计与实现的主要内容,如果未能解决你的问题,请参考以下文章
