51nod 1463 找朋友（线段树+离线处理）

Posted 2020-10-04 谦谦君子，陌上其华

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1463

题意：

 

思路：

好题！

先对所有查询进行离线处理，按照右区间排序，因为k一共最多只有10个，所有在该区间内的B数组，每次枚举K值，通过这样的方式来得到另外一个B值。但是这样得到的B值它在B数组中的位置必须在当前数的左边。如下图：（j为当前数在B数组中的位置，pos为计算得到的另一个B值在数组中的位置）

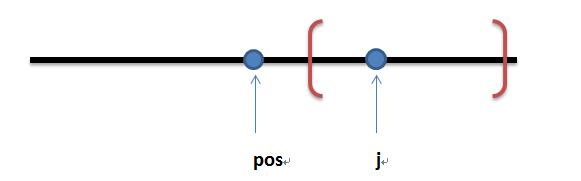
这两个数的和记录在pos中，这里pos的位置必须在j的左边，假设第q个查询区间如上图所示（请在脑中将pos和j互换一下），那么此时j就没包含在该区间内，这样一来，查询得到的值就会有错。因为我们是按照右区间排序的，所以右区间会不断扩大，只要左边被覆盖的，那么右边的数肯定是在该区间内的。

用线段树维护即可。具体请参见代码。

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<cstring>
  4 #include<cstdio>
  5 #include<vector>
  6 #include<stack>
  7 #include<queue>
  8 #include<cmath>
  9 #include<map>
 10 #include<set>
 11 using namespace std;
 12 typedef long long ll;
 13 const int INF = 0x3f3f3f3f;
 14 const int maxn=1e5+5;
 15 
 16 int n,q,m;
 17 int A[maxn],B[maxn],K[15],B_pos[maxn],ans[maxn];
 18 
 19 struct node
 20 {
 21     int l,r,id;
 22     bool operator<(const node& rhs) const
 23     {
 24         return r<rhs.r;
 25     }
 26 }Q[maxn];
 27 
 28 int MAX[maxn<<2];
 29 int val[maxn<<2];
 30 
 31 void build(int l, int r, int o)
 32 {
 33     val[o]=0;
 34     if(l==r)  return;
 35     int mid=(l+r)>>1;
 36     build(l,mid,o<<1);
 37     build(mid+1,r,o<<1|1);
 38 }
 39 
 40 void update(int l, int r, int pos, int x, int o)
 41 {
 42     val[o]=max(val[o],x);
 43     if(l==pos && r==pos)  return;
 44     int mid=(l+r)>>1;
 45     if(pos<=mid)  update(l,mid,pos,x,o<<1);
 46     else   update(mid+1,r,pos,x,o<<1|1);
 47 }
 48 
 49 int query(int ql, int qr, int l, int r, int o)
 50 {
 51     if(ql<=l && qr>=r)  return val[o];
 52     int mid=(l+r)>>1;
 53     int res=0;
 54     if(ql<=mid)  res=max(res,query(ql,qr,l,mid,o<<1));
 55     if(qr>mid)   res=max(res,query(ql,qr,mid+1,r,o<<1|1));
 56     return res;
 57 }
 58 
 59 int main()
 60 {
 61    //freopen("in.txt","r",stdin);
 62     scanf("%d%d%d",&n,&q,&m);
 63     for(int i=1;i<=n;i++)  scanf("%d",&A[i]);
 64     for(int i=1;i<=n;i++)  {scanf("%d",&B[i]);B_pos[B[i]]=i;}
 65     for(int i=1;i<=m;i++)  scanf("%d",&K[i]);
 66     for(int i=1;i<=q;i++)
 67     {
 68         scanf("%d%d",&Q[i].l,&Q[i].r);
 69         Q[i].id=i;
 70     }
 71     sort(Q+1,Q+q+1);
 72     build(1,n,1);
 73     int s=1;
 74     memset(MAX,0,sizeof(MAX));
 75     for(int i=1;i<=q;i++)
 76     {
 77         int r=Q[i].r;
 78         for(int j=s;j<=r;j++)
 79         {
 80             for(int k=1;k<=m;k++)
 81             {
 82                 int tmp_B=B[j]+K[k];
 83                 int pos=B_pos[tmp_B];  //得到tmp_B在B数组中的位置
 84                 if(tmp_B<=n && pos<j && A[pos]+A[j]>MAX[pos])
 85                 {
 86                     MAX[pos]=A[pos]+A[j];  //此时pos位置的最大值是由pos和[1,j)之间的一个数相加而成
 87                     update(1,n,pos,MAX[pos],1); //更新线段树
 88                 }
 89                 tmp_B=B[j]-K[k];
 90                 pos=B_pos[tmp_B];
 91                 if(tmp_B>=1 && pos<j && A[pos]+A[j]>MAX[pos])
 92                 {
 93                     MAX[pos]=A[pos]+A[j];
 94                     update(1,n,pos,MAX[pos],1);
 95                 }
 96             }
 97         }
 98         ans[Q[i].id]=query(Q[i].l,Q[i].r,1,n,1); //查询该区间内的最大值
 99         s=r;
100     }
101     for(int i=1;i<=q;i++)  printf("%d\\n",ans[i]);
102     return 0;
103 }

 

再给一个树状数组的吧，按照左区间从大到小排序。

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<vector>
 6 #include<stack>
 7 #include<queue>
 8 #include<cmath>
 9 #include<map>
10 #include<set>
11 using namespace std;
12 typedef long long ll;
13 const int INF = 0x3f3f3f3f;
14 const int maxn=1e5+5;
15 
16 int n,q,m;
17 int A[maxn],B[maxn],K[15],B_pos[maxn],ans[maxn],c[maxn];
18 
19 struct node
20 {
21     int l,r,id;
22     bool operator<(const node& rhs) const
23     {
24         return l>rhs.l;
25     }
26 }Q[maxn];
27 
28 int lowbit(int x)
29 {
30     return x&(-x);
31 }
32 
33 int find_max(int x)
34 {
35     int res=0;
36     while(x>0)
37     {
38         res=max(res,c[x]);
39         x-=lowbit(x);
40     }
41     return res;
42 }
43 
44 void update(int x, int val)
45 {
46     while(x<=n)
47     {
48         c[x]=max(c[x],val);
49         x+=lowbit(x);
50     }
51 }
52 
53 int main()
54 {
55     //freopen("in.txt","r",stdin);
56     scanf("%d%d%d",&n,&q,&m);
57     for(int i=1;i<=n;i++)  scanf("%d",&A[i]);
58     for(int i=1;i<=n;i++)  {scanf("%d",&B[i]);B_pos[B[i]]=i;}
59     for(int i=1;i<=m;i++)  scanf("%d",&K[i]);
60     for(int i=1;i<=q;i++)
61     {
62         scanf("%d%d",&Q[i].l,&Q[i].r);
63         Q[i].id=i;
64     }
65     sort(Q+1,Q+q+1);
66     memset(c,0,sizeof(c));
67     int s=n+1;
68     for(int i=1;i<=q;i++)
69     {
70         for(int j=s-1;j>=Q[i].l;j--)
71         {
72             for(int k=1;k<=m;k++)
73             {
74                 int tmp_B=B[j]+K[k];
75                 int pos=B_pos[tmp_B];
76                 if(tmp_B<=n && pos>j)
77                 {
78                     update(pos,A[pos]+A[j]);
79                 }
80                 tmp_B=B[j]-K[k];
81                 pos=B_pos[tmp_B];
82                 if(tmp_B>=1 && pos>j)
83                 {
84                     update(pos,A[pos]+A[j]);
85                 }
86             }
87         }
88         s=Q[i].l;
89         ans[Q[i].id]=find_max(Q[i].r);
90     }
91 
92     for(int i=1;i<=q;i++)  printf("%d\\n",ans[i]);
93     return 0;
94 }