《opencv实战》 之 局部极值提取
Posted 寂寞的小乞丐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《opencv实战》 之 局部极值提取相关的知识,希望对你有一定的参考价值。
局部极值提取算法
这是http://www.imagepy.org/的作者原创,我只是对其理解之后改进和说明,欢迎大家使用这个小软件!
有需要C++的朋友,可有留邮箱,经测试和改进的版本!
算法原理:(按照程序思路来,当然其中很多可以改进的地方)
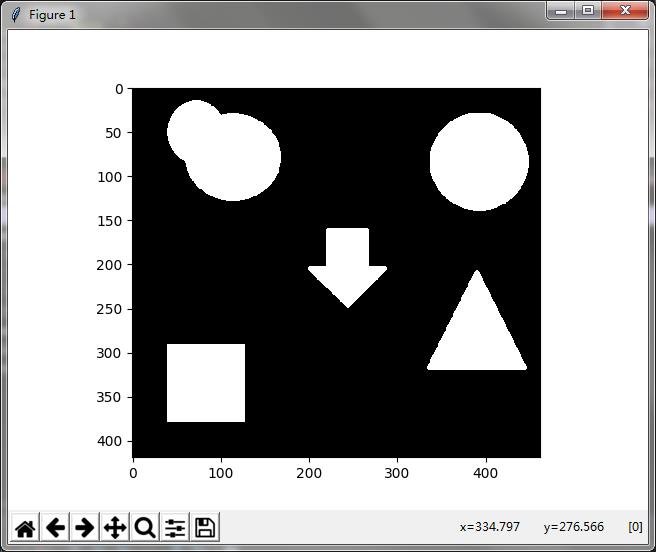
第一步:
先进行距离变换(这类问题都是要通过几何操作进行,距离变换就是几何距离)
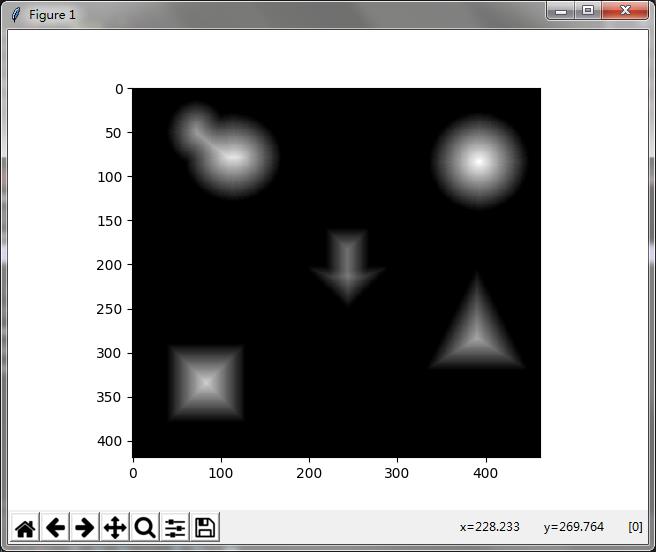
第二步:
先找全局可能最大值,然后对图像进行标记
全局可能最大值是基础,3X3核在图像上滑动去找全局可能最大值。标记是为了掩膜操作更方便,你看opencv很多函数都有掩膜,PS上面也有那个白色的膜。
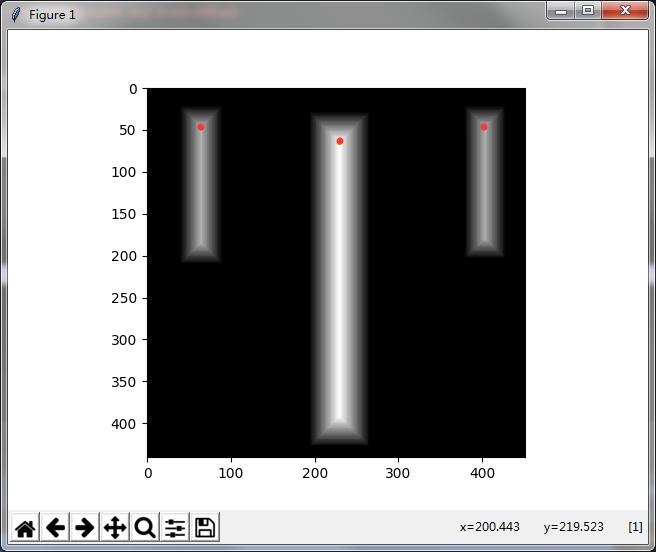
图片结果是:背景和最大值标记3,前景标记1,图像边界标记0(为了防止越界)
貌似下面的图片显示有问题,matploylib的显示有时候确实有问题,Debug的时候就和显示不一样,没关系这一步比较简单。
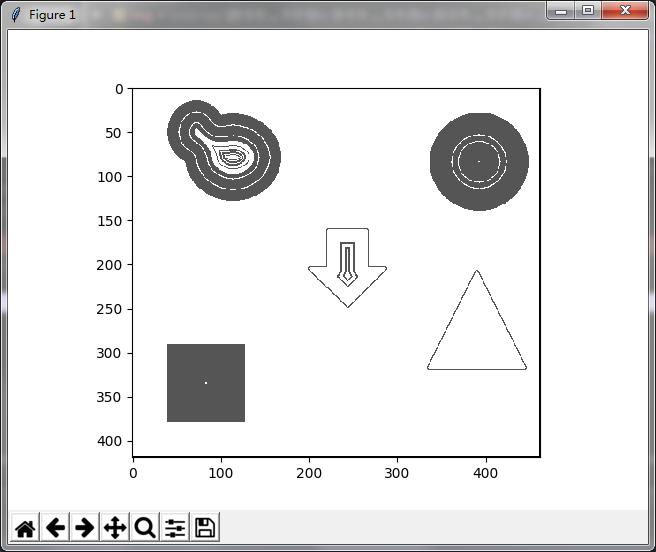
第三步:
对全局可能最大值进行排除,这一步是程序核心!这里以求最大值为例,最小值相反。
-
-
-
-
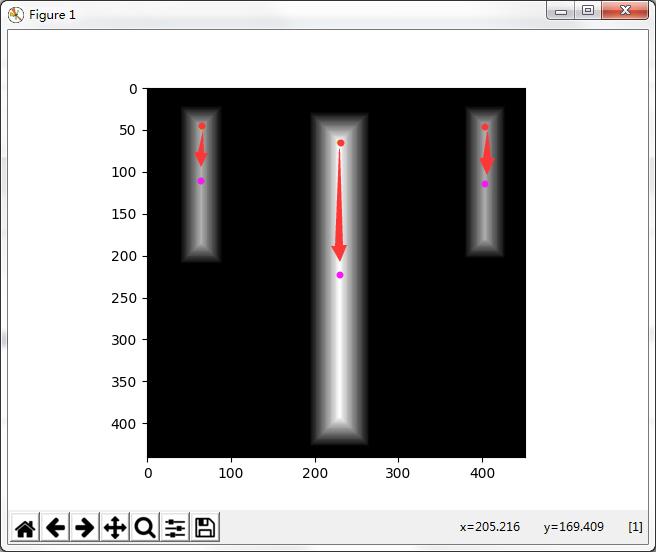
- 首先对找到的最大值进行排序--从大到小
- 按照从大到小的顺序去寻找每个最大值的领地
- 领地按照“目标范围”和“目标深度”两个原则,具体表现形式为:“不重合”、“不包括”、“领主大于等于领地”
-
-
-
下面以图说明两个大原则:
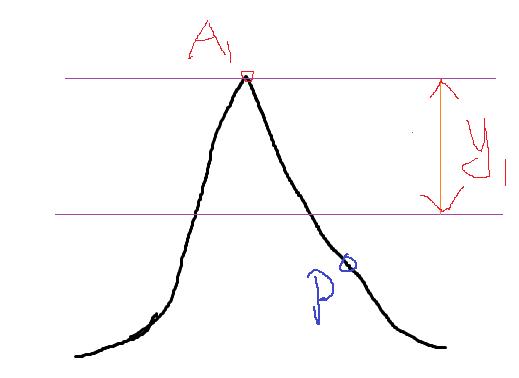
目标范围:
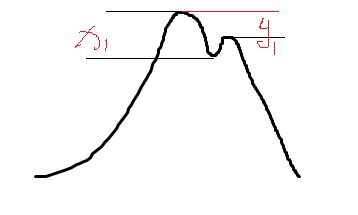
下图A1这个最大最他所占领的范围由用户输入,假设半径为y,则 x1 = x2 = y ,x1和x2的范围就是A1的范围,P点虽然很低,但是不属于A1的范围,所以不去占领。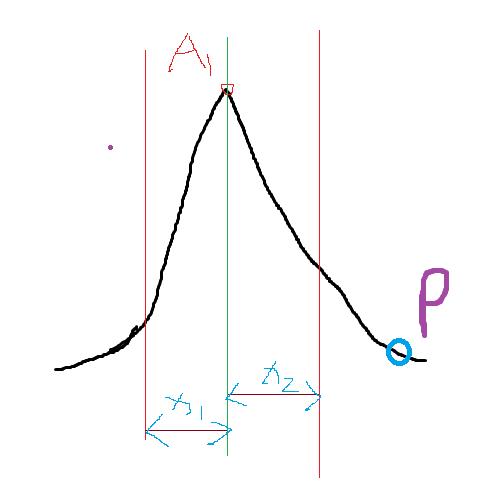
目标深度:
下图A1的深度也又用户输入,假设输入为y,则 y1 = y,高度确定之后,那么P点虽然也在山脊上,但是不会被A1所占领。
下面以图为例进一步说明三个具体形式:
注释:三个具体形式是建立在两个原则之上的,所以理解上面是结局算法的基础。
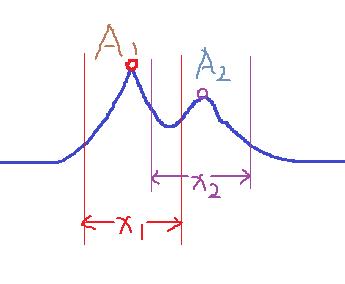
不重合形式:
下图A1和A2有领土纠纷,但是A1峰值高所以先进行领地划分,当A2进行领地划分的时候一旦接触A1的领地就立马被消灭,最后只剩A1的存在。
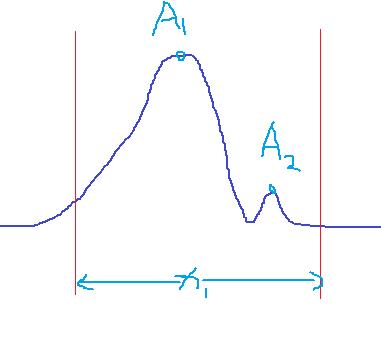
不包括形式:
下图A1先进行领土划分,过程中直接把A2消灭了,不存在A2的领土划分
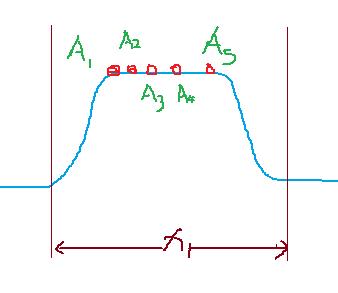
领主大于等于领地形式,也可以叫同等峰值先来先得形式:
由于A1先进行领土划分,所以后面的都被消灭了,读到这里你会发现这个程序的BUG,后面再详细谈论这一点
目标深度原则:
要确定和你预定的深度是不是符合,比如你想要山峰之间的深度都是在10cm以上,那么有些不符合的就得去除,去除原则肯定矮的GG
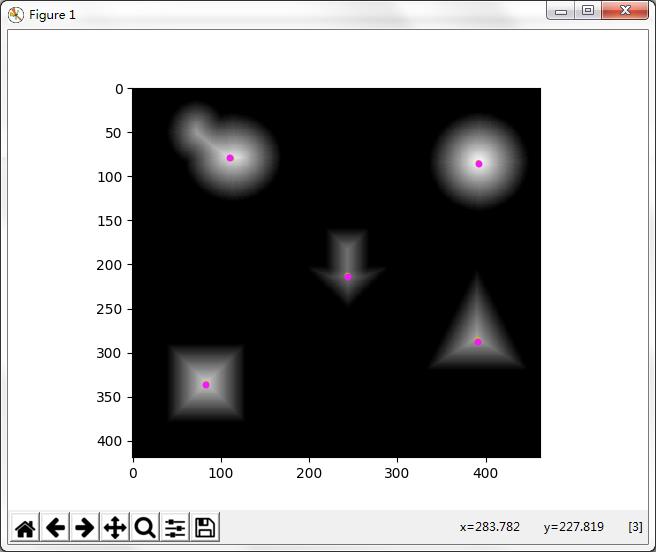
注释:大佬的程序没有几何距离,还有部分Bug,部分经过修正了。
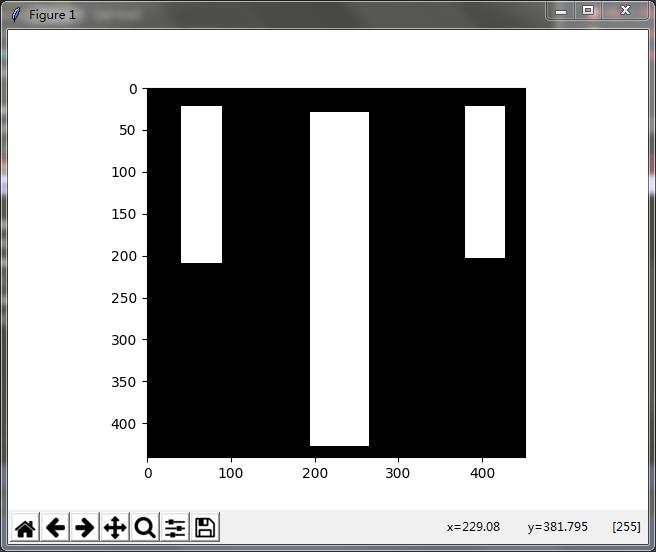
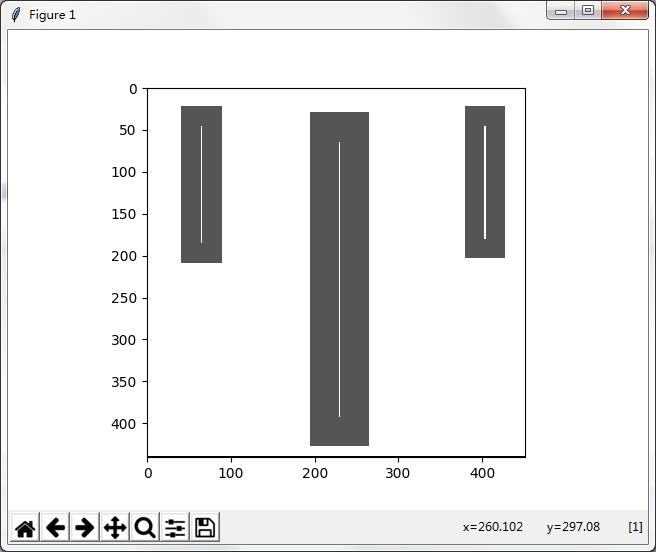
程序有待改进:
这部分可以通过处理---“同样的峰值且山脉相连”的一类极值点,对其平均、覆盖范围最多等操作取一个中间的值!
由于python用的不熟练,而且现在时间太晚了脑子转不动,以后用C++写的时候再改进这一点。
2017.10.17更新:

1.对上面第二步:可能最大值进行补充
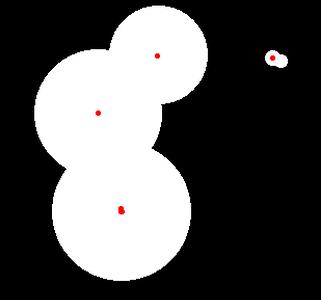
请看下面这个图,中间位置肯定不是最大值区域,而且通过上面的第三步过滤也是没办法过滤的,具体看上面原理就知道了,所以需要在第二步进行过滤!
本程序利用如下方法:
A.每一层的最大值都大于外面一层,sum[0]>=sum[1] && sum[1]>sum[2] && sum[2]>sum[3],这里使用到9X9的内核
B.记录每一层最大值出现的位置X0和X1,然后最大值的距离(abs(x0.x - x1.x) <= 2 && abs(x0.y - x1.y) <= 2)小于等于2,这里不严谨,因为每层最大值不止一个。
C.记录最大值出现的数量n_count >= 3
1 float sum[4] = { 0 };//存储最大值进行对比、在这里说不清楚看博客2017.10.17更新 2 sum[0] = img[3][j]; 3 Point x0 = Point(0, 0); 4 Point x1 = Point(0, 0); 5 uchar n_count = 0; 6 for (int m = 2; m < 5; m++) 7 { 8 for (int n = -1; n < 2; n++) 9 { 10 if (m == 3 && n == 0) continue; 11 sum[1] = sum[1] < img[m][j + n] ? img[m][j + n] : sum[1]; 12 x0 = sum[0] == img[m][j + n] ? Point(m, n) : x0; 13 n_count = sum[0] == img[m][j + n] ? n_count+1 : n_count; 14 //flag = img[3][j + 0] < img[m][j + n] ? true : flag;//如果目标像素小于周围任何一个像素就说明这个一定不是最大值 15 } 16 } 17 for (int m = 1; m < 6; m++) 18 { 19 for (int n = -2; n < 3; n++) 20 { 21 if (2 <= m && m <= 4 && -1 <= n && n <= 1) continue; 22 sum[2] = sum[2] < img[m][j + n] ? img[m][j + n] : sum[2]; 23 x1 = sum[0] == img[m][j + n] ? Point(m, n) : x1; 24 n_count = sum[0] == img[m][j + n] ? n_count+1 : n_count; 25 //flag = img[3][j + 0] < img[m][j + n] ? true : flag;//如果目标像素小于周围任何一个像素就说明这个一定不是最大值 26 } 27 } 28 for (int m = 0; m < 7; m++) 29 { 30 for (int n = -3; n < 4; n++) 31 { 32 sum[3] = sum[3] < img[m][j + n] && !(1 <= m && m <= 5 && -2 <=n && n <= 2) ? img[m][j + n] : sum[3]; 33 //flag = img[3][j+0] < img[m][j + n] ? true : flag;//如果目标像素小于周围任何一个像素就说明这个一定不是最大值 34 } 35 } 36 x1 = (x1.x == 0 && x1.y == 0) || n_count >= 3 ? x0 : x1;//判断是否存在5X5的最大值(和目标点相同) 37 int tmp = sum[0] >= sum[1] && sum[1] >= sum[2] && sum[2] >= sum[3] && (abs(x0.x - x1.x) <= 2 && abs(x0.y - x1.y) <= 2) 38 ? 0 : FillBlock(src, mask_tmp, Point(j, i));//tmp没意义,就是为了调用后面的函数而已 39 }


2.对第三步进行补充
A.搜索过程遇到边界,那就把这个最大值点去除if (img[i][fill_point[count].x + j] == 2 || msk[i][fill_point[count].x + j] == 0) max_point[k].data = 1;
3.效果图
注释:满足一个条件就判定为最大值!
1 Find_Max(img, mask,0, 5000);
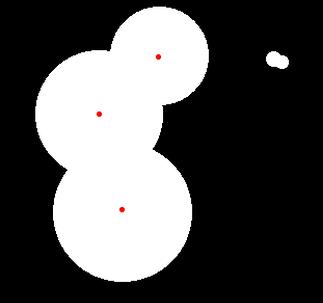
1 Find_Max(img, mask,5000, 0); 
1 Find_Max(img, mask,5000, 5000);

1 Find_Max(img, mask,10, 20);

1 Find_Max(img, mask,10, 50);
1 import scipy.ndimage as ndimg 2 import numpy as np 3 from numba import jit 4 import cv2 5 6 def neighbors(shape): 7 dim = len(shape) 8 block = np.ones([3] * dim) 9 block[tuple([1] * dim)] = 0 10 idx = np.where(block > 0) 11 idx = np.array(idx, dtype=np.uint8).T 12 idx = np.array(idx - [1] * dim) 13 acc = np.cumprod((1,) + shape[::-1][:-1]) 14 return np.dot(idx, acc[::-1]) 15 16 17 @jit # trans index to r, c... 18 19 def idx2rc(idx, acc): 20 rst = np.zeros((len(idx), len(acc)), dtype=np.int16) 21 for i in range(len(idx)): 22 for j in range(len(acc)): 23 rst[i, j] = idx[i] // acc[j] 24 idx[i] -= rst[i, j] * acc[j] 25 return rst 26 27 28 #@jit # fill a node (may be two or more points) 29 30 def fill(img, msk, p, nbs, buf): 31 msk[p] = 3 32 buf[0] = p 33 back = img[p] 34 cur = 0 35 s = 1 36 while cur < s: 37 p = buf[cur] 38 for dp in nbs: 39 cp = p + dp 40 if img[cp] == back and msk[cp] == 1: 41 msk[cp] = 3 42 buf[s] = cp 43 s += 1 44 if s == len(buf): 45 buf[:s - cur] = buf[cur:] 46 s -= cur 47 cur = 0 48 cur += 1 49 #msk[p] = 3 50 51 52 #@jit # my mark 53 54 def mark(img, msk, buf, mode): # mark the array use (0, 1, 2) 55 omark = msk 56 nbs = neighbors(img.shape) 57 idx = np.zeros(1024 * 128, dtype=np.int64) 58 img = img.ravel() # 降维 59 msk = msk.ravel() # 降维 60 s = 0 61 for p in range(len(img)): 62 if msk[p] != 1: continue 63 flag = False 64 for dp in nbs: 65 if mode and img[p + dp] > img[p]: 66 flag = True 67 break 68 elif not mode and img[p + dp] < img[p]: 69 flag = True 70 break 71 72 if flag : continue 73 else : fill(img, msk, p, nbs, buf) 74 idx[s] = p 75 s += 1 76 if s == len(idx): break 77 plt.imshow(omark, cmap=\'gray\') 78 return idx[:s].copy() 79 80 81 82 def filter(img, msk, idx, bur, tor, mode): 83 omark = msk 84 nbs = neighbors(img.shape) 85 acc = np.cumprod((1,) + img.shape[::-1][:-1])[::-1] 86 img = img.ravel() 87 msk = msk.ravel() 88 89 arg = np.argsort(img[idx])[::-1 if mode else 1] 90 91 for i in arg: 92 if msk[idx[i]] != 3: 93 idx[i] = 0 94 continue 95 cur = 0 96 s = 1 97 bur[0] = idx[i] 98 while cur < s: 99 p = bur[cur] 100 if msk[p] == 2: 101 idx[i] = 0 102 break 103 104 for dp in nbs: 105 cp = p + dp 106 if msk[cp] == 0 or cp == idx[i] or msk[cp] == 4: continue 107 if mode and img[cp] < img[idx[i]] - tor: continue 108 if not mode and img[cp] > img[idx[i]] + tor: continue 109 bur[s] = cp 110 s += 1 111 if s == 1024 * 128: 112 cut = cur // 2 113 msk[bur[:cut]] = 2 114 bur[:s - cut] = bur[cut:] 115 cur -= cut 116 s -= cut 117 118 if msk[cp] != 2: msk[cp] = 4 119 cur += 1 120 msk[bur[:s]] = 2 121 #plt.imshow(omark, cmap=\'gray\') 122 123 return idx2rc(idx[idx > 0], acc) 124 125 126 def find_maximum(img, tor, mode=True): 127 msk = np.zeros_like(img, dtype=np.uint8) 128 msk[tuple([slice(1, -1)] * img.ndim)] = 1 129 buf = np.zeros(1024 * 128, dtype=np.int64) 130 omark = msk 131 idx = mark(img, msk, buf, mode) 132 plt.imshow(msk, cmap=\'gray\') 133 idx = filter(img, msk, idx, buf, tor, mode) 134 return idx 135 136 137 if __name__ == \'__main__\': 138 from scipy.misc import imread 139 from scipy.ndimage import gaussian_filter 140 from time import time 141 import matplotlib.pyplot as plt 142 143 img = cv2.imread(\'123.png\') 144 img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) 145 ret2, img = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU) 146 img[:] = ndimg.distance_transform_edt(img) 147 plt.imshow(img, cmap=\'gray\') 148 pts = find_maximum(img, 20, True) 149 start = time() 150 pts = find_maximum(img, 10, True) 151 print(time() - start) 152 plt.imshow(img, cmap=\'gray\') 153 plt.plot(pts[:, 1], pts[:, 0], \'y.\') 154 plt.show()
C++版本
老版本、不稳定,可以看思路

1 //---fill black value 2 int FillBlock(Mat src, Mat &mask, Point center) 3 { 4 uchar back = src.at<uchar>(center.y, center.x); 5 vector<Point> fill_point; 6 int count = 0, count_mount = 1; 7 fill_point.push_back(center); 8 while (count < count_mount) 9 { 10 vector<uchar*> img; 11 vector<uchar*> msk; 12 for (int i = -1; i < 2; i++) 13 { 14 img.push_back(src.ptr<uchar>(fill_point[count].y + i)); 15 msk.push_back(mask.ptr<uchar>(fill_point[count].y + i)); 16 } 17 for (size_t i = 0; i < 3; i++) 18 { 19 for (int j = -1; j < 2; j++) 20 { 21 if (img[i][fill_point[count].x + j] == back && !(j == 0 && i == 1) && msk[i][fill_point[count].x + j] == 255) 22 { 23 fill_point.push_back(Point(fill_point[count].x + j, fill_point[count].y + i - 1)); 24 msk[i][fill_point[count].x + j] = 1; 25 } 26 } 27 } 28 msk[1][fill_point[count].x] = 1; 29 count_mount = fill_point.size() - 1; 30 fill_point.erase(fill_point.begin()); 31 } 32 return 0; 33 } 34 //---cal mask 35 //---@_src 36 //---@mask 37 void MaskImage(InputArray _src, Mat &mask) 38 { 39 Mat src = _src.getMat(),mask_tmp = Mat::zeros(src.size(), CV_8UC1); 40 mask_tmp.setTo(255); 41 Mat rows = Mat::zeros(Size(src.cols, 1), CV_8UC1), cols = Mat::zeros(Size(1, src.rows), CV_8UC1); 42 Mat src_rows_beg = mask_tmp.row(0); 43 Mat src_rows_end = mask_tmp.row(src.rows - 1); 44 Mat src_cols_beg = mask_tmp.col(0); 45 Mat src_cols_end = mask_tmp.col(src.cols - 1); 46 rows.copyTo(src_rows_beg); rows.copyTo(src_rows_end); 47 cols.copyTo(src_cols_beg); cols.copyTo(src_cols_end); 48 for (size_t i = 1; i < src.rows-1; i++) 49 { 50 uchar *img0 = src.ptr<uchar>(i - 1); 51 uchar *img = src.ptr<uchar>(i); 52 uchar *img1 = src.ptr<uchar>(i + 1); 53 uchar *msk = mask_tmp.ptr<uchar>(i); 54 for (size_t j = 1; j < src.cols-1; j++) 55 { 56 bool flag = false; 57 //msk[j] = img[j] == 0 ? 0 : msk[j]; 58 if (msk[j] != 255) continue; 59 flag = (img[j] < img[j - 1] || img[j] < img[j + 1] 60 || img[j] < img0[j] || img[j] < img0[j - 1] 61 || img[j] < img0[j + 1] || img[j] < img1[j] 62 || img[j] < img1[j - 1] || img[j] < img1[j + 1]) 63 ? true : false; 64 int tmp = flag == true ? FillBlock(src, mask_tmp, Point(j, i)) : 0; 65 } 66 } 67 mask = mask_tmp.clone(); 68 } 69 //---filter parts max value 70 //---@ 71 //---@ 72 //---@gap 73 //---@radius 74 75 vector<Point> Find_Max(InputArray _src, Mat&mask,int gap,int radius) 76 { 77 Mat src = _src.getMat(); 78 79 typedef struct MyStruct 80 { 81 Point position; 82 float data; 83 }MyStruct; 84 85 MaskImage(src, mask); 86 vector<MyStruct> max_point; 87 for (size_t i = 0; i < src.rows; i++) 88 { 89 uchar *img = src.ptr<uchar>(i); 90 uchar *msk = mask.ptr<uchar>(i); 91 for (size_t j = 0; j < src.cols; j++) 92 { 93 if (msk[j] != 255) continue; 94 MyStruct my_struct; 95 my_struct.data = img[j]; 96 my_struct.position = Point(j, i); 97 max_point.push_back(my_struct); 98 } 99 } 100 for (size_t i = 0; i < max_point.size(); i++) 101 { 102 for (size_t j = i; j < max_point.size(); j++) 103 { 104 MyS以上是关于《opencv实战》 之 局部极值提取的主要内容,如果未能解决你的问题,请参考以下文章
OpenCV 例程 300篇247. 特征检测之最大稳定极值区域(MSER)
