汉诺塔算法之求解最佳步数

Posted 2020-10-03 肖薇

写的不好，但是请尊重版权，转载请注明出处： http://www.cnblogs.com/xiaovw/

 

何为汉诺塔？

　　答：汉诺塔是根据一个传说形成的一个问题。汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

 

 

关于汉诺塔的经典问题：

　　有三根相邻的柱子，标号为A,B,C，A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘，要把所有盘子一个一个移动到柱子B上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方，请问至少需要多少次移动。转载请注明出处： http://www.cnblogs.com/xiaovw/

 

题目要求：

　　1.在小圆盘上不能放大圆盘。

　　2.在三根柱子之间一回只能移动一个圆盘。

　　3.只能移动在最顶端的圆盘。

 

算法分析：

　　在这里我们暂且只讨论到达制定目标所需的步数，不讨论移动的步骤。

　　

 

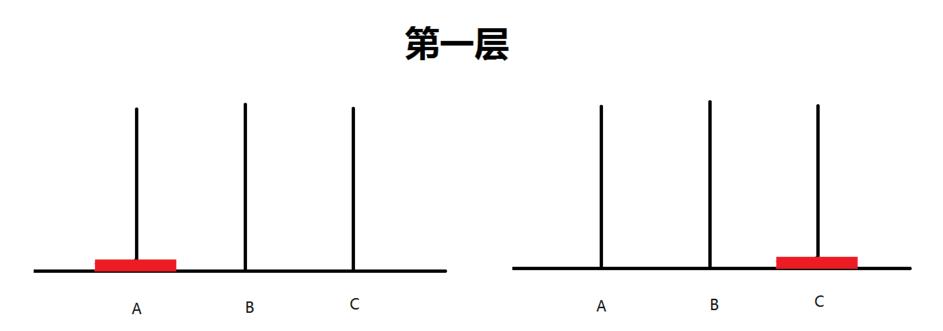
　　当只有一层的时候，只需一步便可从A到C：A -> C

 

 

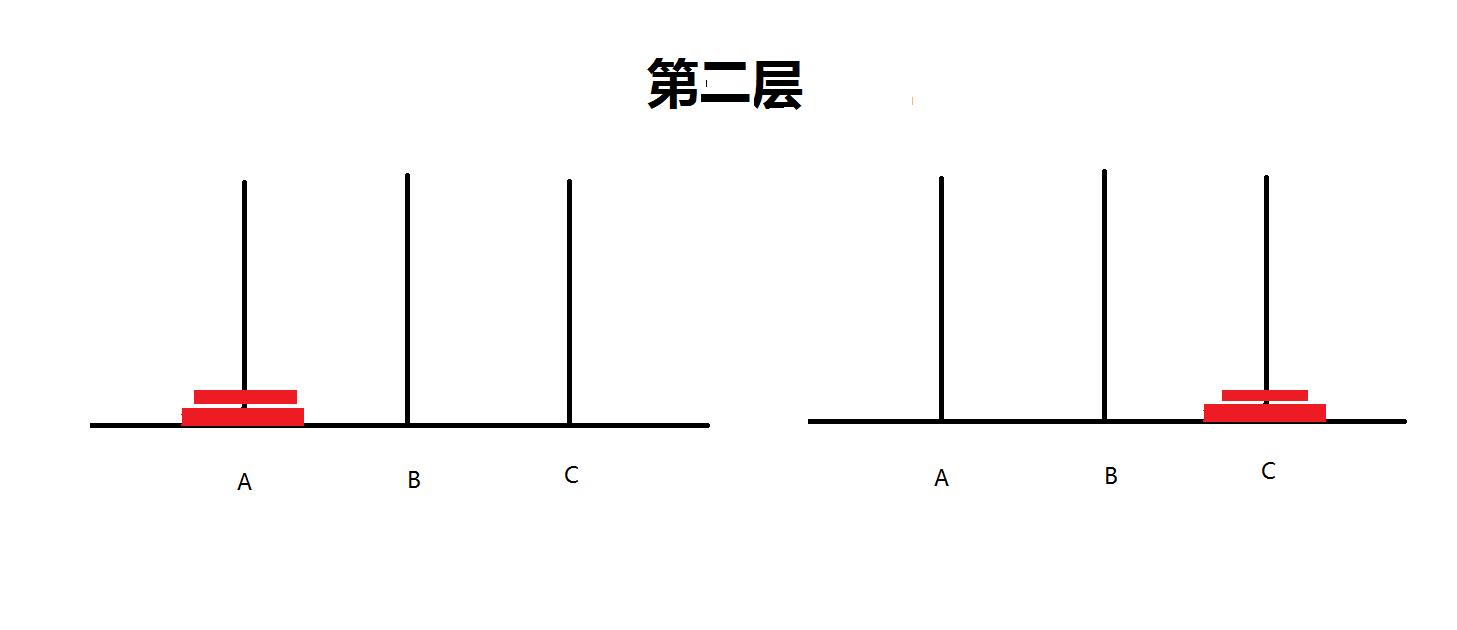
　　第二层将所有的盘子从A移动到C 有3种选择（不做演示，可在此链接内自行进行测试，http://www.4399.com/flash/49864_4.htm）

　　第三层 有7种选择

　　第四层 有15种选择

　　第五层 有31种选择

　　。。。。

　　

　　由此测试数据:

　　　　f( 1 ) = 1;

　　　　f( 2 ) = 3 ;

　　　　f( 3 ) = 7;

　　　　f( 4 ) = 15;

　　　　f( 5 ) = 31;

　　　　.......

　　可发现： f（n）= 2 * f（n-1）+ 1; （注意：测试f(1)时，f(0)=0）

　　　　即：f（n）= 2^n - 1; 

/* f（n）= 2 * f（n-1）+ 1不验证，当64层时，数据长度太长*/
1class Hannuota{
2    public static void main(){
3      
4        Scanner sc= new Scanner(System.in);
5         int n=sc.nextInt;
6        System.out.println("走了"+Math.pow(2,n)-1+"步");
7     }  
8 }    

 

　　　转载请注明出处： http://www.cnblogs.com/xiaovw/