信息学中的数论

Posted 2020-10-03

注：本文章中大多数定理未证明，一因为太过繁琐，二因为我太菜了不会证。

希望得到证明的就请舍弃这篇吧。

 

数论中有一个东西非常常见，也非常烦。

这个东西叫“质数”

（及其相关知识）

那么这一篇来聊聊与质数有关的话题吧：

质数，筛质数的方法，phi函数，线性筛。

 

恩先说质数，

质数就是只有1和它本身两个因数的自然数。

与质数相对的就是合数

好了质数讲完了。

 

筛质数的方法？

判断一个数是否是质数大家都会吧，根号的做法

如果要筛出1到n之间所有的质数呢？

普通的筛法求质数，我们来归纳一下，可以通过筛去合数的方法来筛质数。

如下代码：

for(int i=2;i<=n;++i)
    for(int j=i+i;j<=n;j+=i)
        check[j]=1;

我们来分析一下该算法的复杂度：

n/2+n/3+......+n/n = n*(1/2+1/3+......+1/n)

右边那个括号里面的，是调和级数

有某个结论：1+1/2+......+1/n = ln(n+1)+r  

那么我们把时间复杂度近似地看做为nlogn

 

这种做法在n=10000000的时候显然效率不高。

有什么快速的筛法呢？

请继续阅读，之后的“线性筛”会来讲解。

 

phi函数。

原来是这么写的：“φ”

φ(n)（欧拉函数）表示，小于n的正整数中，与n互质的数的个数，

特别的，φ(1)=1。

由于这个符号比较难打，之后会用phi代替。

这个东西非常有用。

大家也许还记得这个东西：

p为质数时，a^(p-1)%p = 1 （费马小定理）

先告诉你一个非常响亮的结论：

对于互质的正整数a和n，有a^phi(n) % n = 1（欧拉定理）

由于质数p，phi(p)=p-1，

因此费马小定理是欧拉定理的一个特例。

 

我们来看一下phi函数的一些特性：

①，p为质数时，phi(p)=p-1

②，p为质数，n为正整数时，phi(p^n)=p^(p-1)*(p-1)

③，a,b互质时，phi(a*b)=phi(a)*phi(b) （即积性函数）

那么根据以上性质，也许大家能轻易得到phi函数的一个通式：

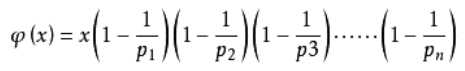
p1,p2,......,pn是x的不同的质因子。

 

 

恩接下来的东西非常重要，

 

 

其实线性筛是个不难的算法，却是个非常优秀的算法；

好了终于要讲线性筛了

我们先来讲线性筛质数

普通筛法求质数是通过筛合数的方法来得到质数，

那能不能把时间复杂度优化到O(n)呢？

这就是线性筛的美妙之处。

假如一个合数90

普通的筛法会使90被其所有的因数筛去，较慢，

我们能否做到，该合数只会被它最小的质因数2筛去，而不是被其他数筛去呢？

如果能做到，那么每个合数被筛去的复杂度是O(1)的，总时间复杂度也就是O(n)的了

我们来看一下代码：

const int N=10000000;
int pn,prime[N+1];        //pn表示质数的个数，prime数组存放质数
bool check[N+1];          //check[i]表示i是否为合数
void getprime()
{
    for(int i=2;i<=N;++i)
    {
        if(!check[i])
        {
            ++pn; p[pn]=i;          //如果i不是合数，加入质数数组
        }
        for(int j=1;j<=pn;++j)
        {
            if(i*p[j]>N)break;      //筛去1到N之间的合数
            check[i*p[j]]=1;        //将合数i*p[j]标记
            if(i%p[j]==0)break;     //使得合数只会被其最小的质因数筛去。
        }
    }
}

 

那么，如何线性筛phi呢？

我们现在需要做的是，用O(n)的时间复杂度，求出phi(1),phi(2),......,phi(n)

首先，来回顾一下phi的性质：

1、积性函数性质

2、x>=1时，phi(p^x)=p^(x-1)*(p-1)

那么，我们能否在线性筛素数的基础上，顺便求phi呢？

对于s是质数次方的情况，可以通过性质2轻松解决，

对于s是合数的情况：

很简单，如果s = p1^s1 * p2^s2 * ...... * pm^sm，p1<p2<...<pm，

那么，根据积性函数性质，我们可以通过phi(s / (p1^s1) ) 求得phi(s)

易得phi(s) = phi( s / (p1^s1) ) * phi(p1 ^ s1)

那么一种做法是，开一个数组f，f[s]=s/(p1^s1) （即把最小质因子全部去除之后的数）

这样，如果s1==1，f[s]=s/p1；否则f[s] = f[s/p1]。（相当于s只会被p1筛去，通过线性筛可以实现）

于是phi(s) = phi(f[s]) * phi(s/f[s])

只要通过线性筛求f数组就可以了。

代码如何实现，

留作思考题（其实是我lazy）