KMP算法入门

Posted 2020-10-03 BobHuang

 

学一把看毛片算法我觉得自己才能变得更加出色

明明昨天的题我都知道怎么模拟了，但是还是不会改KMP，是我学丑了

KMP是Knuth-Morris-Pratt三人设计的线性时间字符串匹配算法

nxt数组的介绍，卧槽，直接找到太爽啦

 

 

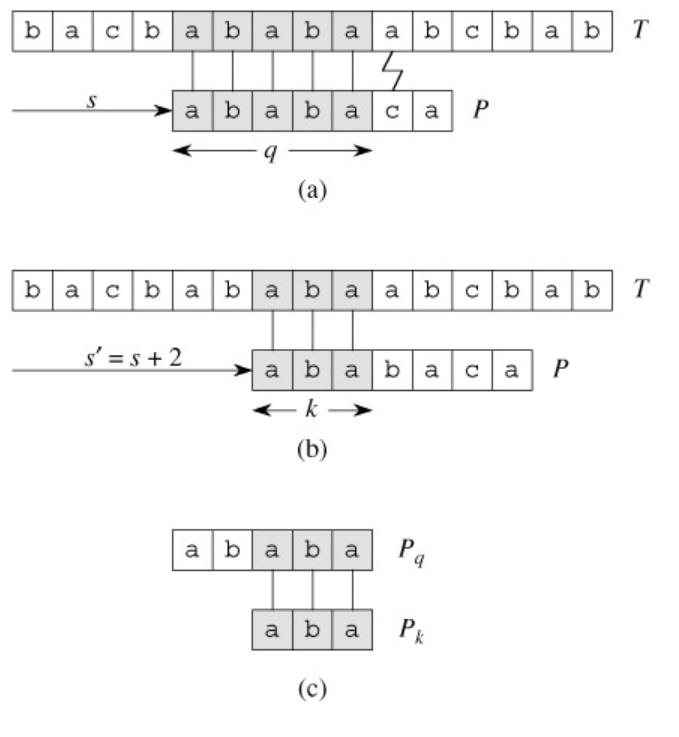
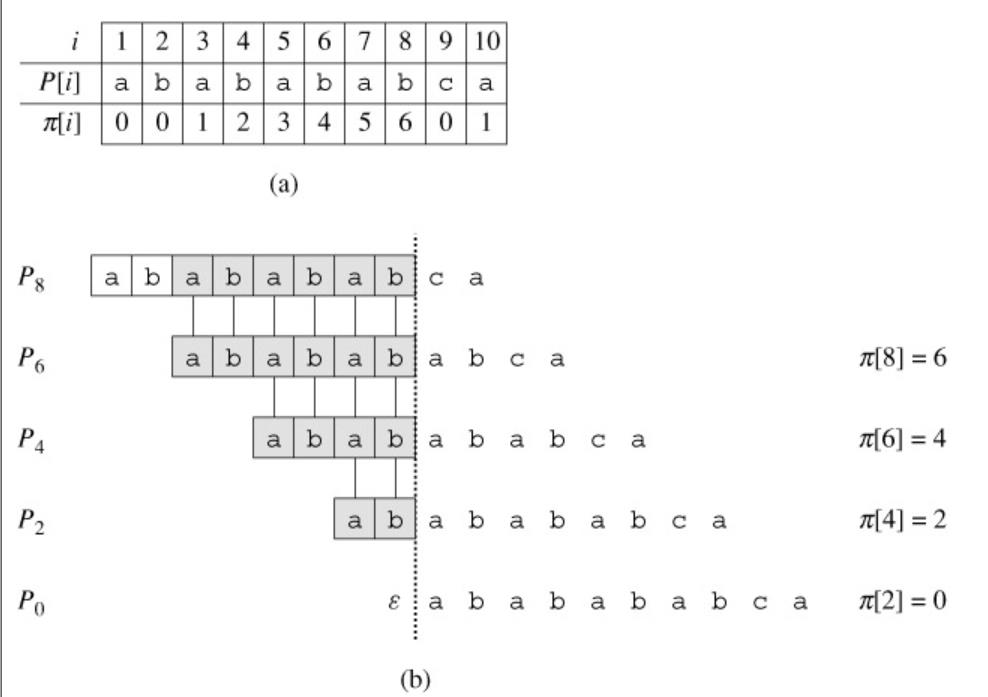
就是我匹配的时候是可以回退的，因为字符的肯能性有限

比如aaaaaaaaab和aaaab进行匹配，aaaab是模式串，aaaaaaaaab是匹配串，我就不用回退那么多次数，因为及时往下推就好了

我匹配了一部分我就能回退到一定的位置

下面是一段演示

我用的求前缀函数

void pre(char *p)
{
    int i,m,j;
    m=strlen(p+1);
    nex[0]=nex[1]=0;
    for(int i=1; i<m; i++)
    {
        j=nex[i];
        while(j&&p[i]!=p[j])j=nex[j];
        nex[i+1]=p[i]==p[j]?j+1:0;
    }
}

aaaab

0 0 1 2 3

aba

0 0 0

就是在字符串匹配时可以回退，因为这些字符和前缀是相同的，所以直接回退就可以的

 

匹配不成功得到的j值

换一组数据

直接匹配就没有回退了

 

 

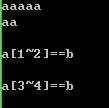
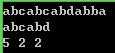
解释下这个复杂些的，就是我往下走啊，但是但匹配到模式串5发现不能继续了，还有两次到2就不能继续了，窝看看nxt可不可以少做些

用来测试的代码

#include <bits/stdc++.h>
using namespace std;
const int N=1000005;
char s[N],t[N];
int nxt[N],sum[N];
void pre(char *p)
{
    int i,m,j;
    m=strlen(p+1);
    nxt[0]=nxt[1]=0;
    for(int i=1; i<m; i++)
    {
        j=nxt[i];
        while(j&&p[i]!=p[j])j=nxt[j];
        nxt[i+1]=p[i]==p[j]?j+1:0;
    }
}
void KMP(char *a,char *b){
    pre(b);
    int j=0;
    int len1=strlen(a+1);
    int len2=strlen(b+1);
    for(int i=0;i<=len1;i++){
        while(j&&a[i]!=b[j+1])
        {printf("%d ",j);j=nxt[j];}
        if(a[i]==b[j+1]) j++;
        if(j==len2){
            printf("\\na[%d~%d]==b\\n",i-len2+1,i);
            j=nxt[j];
        }
    }
}
int main()
{
    scanf("%s",s+1);
    scanf("%s",t+1);
    KMP(s,t);
    return 0;
}

 我的模板

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
char s[N],t[N];
int nxt[N];
void pre(char *t)
{
    int i=0,j=-1;
    nxt[0]=-1;
    while(t[i])
    {
        if(j==-1||t[i]==t[j])
        {
            i++,j++;
            if(t[i]!=t[j])nxt[i]=j;
            else nxt[i]=nxt[j];
        }
        else j=nxt[j];
    }
}
int KMP(char *s,char *t)
{
    pre(t);
    int i=0,j=0;
    while(s[i])
    {
        if(j==-1||s[i]==t[j])i++,j++;
        else j=nxt[j];
    }
    return j;
}
int main()
{
    
    return 0;
}

 

伪代码

KMP-MATCHER(T, P)
 1 n ← length[T]
 2 m ← length[P]
 3 π ← COMPUTE-PREFIX-FUNCTION(P)
 4 q ← 0                          ▹Number of characters matched.
 5 for i ← 1 to n                 ▹Scan the text from left to right.
 6      do while q > 0 and P[q + 1] ≠ T[i]
 7             do q ← π[q]    ▹Next character does not match.
 8         if P[q + 1] = T[i]
 9            then q ← q + 1      ▹Next character matches.
10         if q = m                    ▹Is all of P matched?
11            then print "Pattern occurs with shift" i - m
12                 q ← π[q]    ▹Look for the next match.

COMPUTE-PREFIX-FUNCTION(P)
 1 m ← length[P]
 2 π[1] ← 0
 3 k ← 0
 4 for q ← 2 to m
 5      do while k > 0 and P[k + 1] ≠ P[q]
 6             do k ← π[k]
 7         if P[k + 1] = P[q]
 8            then k ← k + 1
 9         π[q] ← k
10 return π