[POJ 1430] Binary Stirling Number

Posted 2020-10-03

题意

　　$\\left\\{ \\begin{aligned} n \\\\ k \\end{aligned} \\right\\} \\mod 2$ .

　　$n, k \\le 10 ^ 9$ .

 

分析

　　$\\left\\{ \\begin{aligned} 0 \\\\ 0 \\end{aligned} \\right\\} = 1$ .

　　$\\left\\{ \\begin{aligned} n \\\\ k \\end{aligned} \\right\\} = k \\left\\{ \\begin{aligned} n-1 \\\\ k \\end{aligned} \\right\\} + \\left\\{ \\begin{aligned} n-1 \\\\ k-1 \\end{aligned} \\right\\}$ .

 

　　构建与 $\\left\\{ \\begin{aligned} n \\\\ k \\end{aligned} \\right\\}$ 奇偶性相同的函数 $\\delta _n ^ k$ .

　　$\\delta _0 ^ 0 = 1$ .

　　$\\delta _n ^ k = \\left\\{ \\begin{aligned} & \\delta_{n-1} ^ {k-1} + k \\delta_{n-1} ^ k  & , k 为奇数 \\\\ & \\delta _{n-1} ^ {k-1} & , k 为偶数 \\end{aligned} \\right.$ .

 

　　将 $\\delta_n ^ k$ 视为二维平面上的一个点.

　　若 $\\delta_n ^ k$ 能由 $\\delta_x ^ y$ 贡献, 则将点 $(x, y)$ 与点 $(n, k)$ 进行连边.

　　答案即为从 $(0, 0)$ 到 $(n, k)$ 的路径数.

 

　　以 $n = 6, k = 6$ 为例, 画个图进行直观地观察.

　　

 

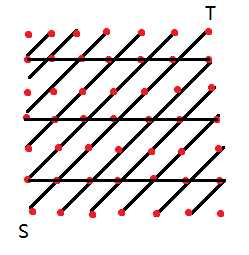
　　发现我们有两种边: $↗$ 和 $→$ , 对应向量 $(+1, +1)$ 与 $(+1, 0)$ .

　　$x↗ + y→ = (x + y, x) = (n, k)$ , 所以 $x = k, y = n-k$ , 即需要走 $k$ 条 $↗$ 边, $n-k$ 条 $→$ 边.

 

　　我们发现一共有 $d = \\left\\{ \\frac{k+1}{2} \\right\\}$ 次机会走 → 边, 每次可以走任意非负整数步.

　　即求不定方程 $a_1 + a_2 + ... + a_d = n-k$ 的非负整数解的个数.

　　通过插板法, 我们得知答案是 $\\binom{n - k + d - 1}{d - 1}$ .

 

　　现在的问题, 变成了计算 $\\binom{n}{m} \\mod 2$ .

　　我们考虑利用 Lucas定理 .

　　将 $n$ 和 $m$ 进行二进制分解, 设 $n = (a_ra_{r-1}a_{r-2}...a_0)_2, m = (b_rb_{r-1}b_{r-2}...b_0)_2$ .

　　那么 $\\binom{n}{m} \\equiv \\prod_{i = 0} ^ r \\binom{a_i}{b_i} (\\mod 2)$ .

 

　　对于每一项 $\\binom{a_i}{b_i}$ , 一共只有 $2 \\times 2$ 中情况.

　　我们考虑列出来, 找到等价的表达式.

　　$\\binom{0}{0} = 1, \\binom{0}{1} = 0, \\binom{1}{0} = 1, \\binom{1}{1} = 1$ .

　　找规律发现 $\\binom{a_i}{b_i} = [a_i ~ and ~ b_i = b_i]$ .

　　

　　所以 $\\binom{n}{m} \\equiv \\prod_{i = 0} ^ r [a_i ~ and ~ b_i = b_i]$ .

　　而对于位运算来说, 不同位的运算是独立的, 所以 $\\binom{n}{m} \\equiv [n ~ and ~ m = m](\\mod 2)$ .

 

实现

 1 #include <cstdio>
 2 int main(void) {
 3     int nT, t, n, k, d; long long a, b;
 4     scanf("%d", &nT);
 5     for (t = 1; t <= nT; t++) {
 6         scanf("%d %d", &n, &k), d = (k+1)>>1;
 7         a = n - k + d - 1, b = d - 1;
 8         printf("%d\\n", (a & b) == b);
 9     }
10     return 0;
11 }