有理数(Rational Number)

Posted 2020-10-03

先来两图╮(╯▽╰)╭大概概述一下层次关系:

 

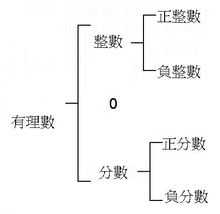
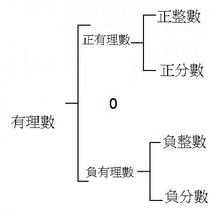
简单来说，能表示为分数(整数除以整数)的数，就是有理数。整数和小数皆能表示为分数形式，所以它们都是有理数:

 

 

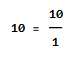
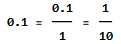
小数分为有限小数，和无限小数两种。而无限小数又分为无限循环小数和无限不循环小数两种。其中我主要想说的是，无限循环小数是能化为有限小数的，所以无限循环小数也属于有理数:

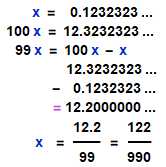
首先，x 是一个无限循环小数，小数点后的循环节3232 是无限重复出现的(不重复出现就是无限不循环小数)，正因为它是重复出现的，也就是代表它是可预测的，那么也就代表可以消去这些循环节。那100x 是怎么来的? 为何是100? 认真看你就知道了，其实100 不是凭空而来的，两边同时乘以100后的数，你会发现，它右侧的数的循环节刚好与x 的循环节一对一对齐了，只要它能对齐无限循环小数的循环节，你T喵╮(╯▽╰)╭想两边同时乘以任何数都可以(但应该不包含0)，没人规定是100，但这个数一遍来说，都是10 的幂次方。100x - x 后遍消去了循环节，变成了一个有限小数，那么再类似解方程的方式解决即可。

 

然而无限不循环小数的循环节是无法预测的，所以也无法被对齐，所以就不能转为有限小数，也就不能化为分数，也就不是有理数。因此→_→，它也被称为无理数(Irrational Number)。

 

最后再总结一下，能化为分数的数就是有理数；反之就是无理数。而所谓的实数(Real Number) 就是有理数和无理数的总称；高中还有个玩意叫虚数(Imaginary Number)。