KMP算法——从入门到懵逼到了解

Posted 2020-10-03 jhcelue

本博文參考http://blog.csdn.net/v_july_v/article/details/7041827
关于其它字符串匹配算法见http://blog.csdn.net/WINCOL/article/details/4795369

暴力匹配算法

    暴力匹配的思路。如果如今文本串S匹配到 i 位置，模式串P匹配到 j 位置。则有：

• 假设当前字符匹配成功（即S[i] == P[j]）。则i++，j++。继续匹配下一个字符；
• 假设失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。

KMP算法概述

KMP算法用于字符串匹配问题，核心思想是找到子串中的反复出现的连续字符并将其记录到数组中。通过这样的方式降低失配后回溯长度，以降低匹配次数。

KMP算法事实上是基于暴力匹配。并加上next数组之后的成果。

通俗易懂的解释见：点击打开链接（这是理解后面内容的基础）

KMP算法过程

如果如今文本串S匹配到 i 位置。模式串P匹配到 j 位置，则有：

• 假设当前字符匹配成功（即S[i] == P[j]）。则i++。j++。继续匹配下一个字符。
• 假设失配（即S[i]! = P[j]），令i = i - (j - 1)。j = 0。相当于每次匹配失败时，j回溯到next[j]

能够发现：KMP算法和暴力匹配算法（BF算法）差别在于KMP算法中i不须要回溯且j回溯到next[j]的位置。

看过上面blog中通俗的解释之后，我们大概理解了KMP算法的核心思想，大概也能写出部分匹配值表。如今我们来搞懂next数组和部分匹配值表的关系。（此处搬来那篇博文中的这个表）

我们所用的移位公式为：

移动位数 = 已匹配的字符数 - 相应的部分匹配值

所以j每次回溯的移动位数就是已经匹配的字符数-相应匹配值，由于对于同一个字符串来

说，每一个字符的这些相关信息是固定的，我如今仅仅须要把这个信息放在一个数组里，每次

须要移动时候就直接让j等于相应位置的移动位数信息,这不就轻松加愉快了。因为每次都

通过这个数组j能够移动到它须要去的下一个位置，所以我们最好还是将其称为next组，每次执

行的过程就是是j=next[j]

那我们如今就要考虑怎样构建next数组。

那么问题就来了，我们移动的位数（即下次j将要去的地方）和当前的字符匹配值并没有什么

卵关系，它仅仅在乎已经匹配了的那个字符相关的信息。既然它不在乎我。那我还管它干嘛，

那么我们所须要的当前移动位数就和当前字符没啥关系了，是时候say goodbye了。

可是尽管说当前匹配值和当前移动位数已经没什么关系了。它却影响了下一个位置的移动

位数，所以我们要将它和下一个位置关联起来。

如此一来。每一个当前位置的移动位数都与

前面的匹配值相关。而下一个位置的移动位数又与当前匹配值相关……我们自然而然就明确了

，我仅仅要将table表中的部分匹配值都右移一位，就能够得到next表了。

那么如今给我们一个字符串。我们就能够自己推出它的next数组了。

基本工作已经完毕了一

半，如今我们的任务就是通过代码的方式写出求next数组的基本方法：

基于之前的理解，我们能够明确next数组是能够通过递推求出的：

1.假设对于值k，已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1，相当于next[j] = k。

即字符串開始的k-1个和当前位置j之前的k-1个相应相等。那么j下一次回溯的位置就是这个k

（由于前面部分都一致。再进行一遍就是无效回溯了）

2.依据已知的next[0...j]求next[j+1]

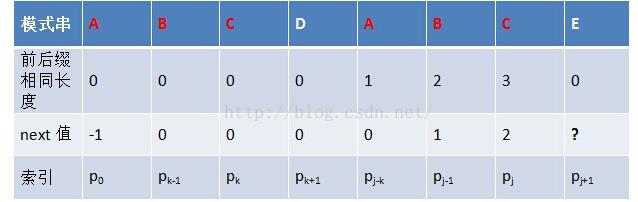
1）首先。若p[k]==p[j]，则next[j+1]=next[j]+1=k+1;

这个非常好理解，就是仅仅要同样就+1即可了。

比方下图中C和C相等，所以next[j+1]=2+1=3;

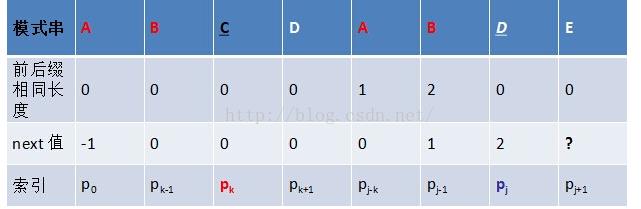
2）若p[k]!=p[j]，k索引next[k]直到与p[j]相等。此时可用公式next[j+1]=k+1（不能用

next[j+1]=next[j]+1。由于此时k已经变了，所以next[j]已经和k不相等了），若没有，则为0

理解起来就是：假设当前的字符不匹配，那么须要寻找长度更短的前缀后缀，让j回溯到

对应的位置（例如以下图）

为何递归前缀索引k = next[k]。就能找到长度更短的同样前缀后缀呢？

这又归根到next数组的含义。我们拿前缀 p0 pk-1 pk 去跟后缀pj-k pj-1 pj匹配，

假设pk 跟pj 失配，下一步就是用p[next[k]] 去跟pj 继续匹配，假设p[ next[k] ]跟pj还是不匹配。则须要寻找长度更短的同样前缀后缀，即下一步用p[ next[ next[k] ] ]去跟pj匹配。

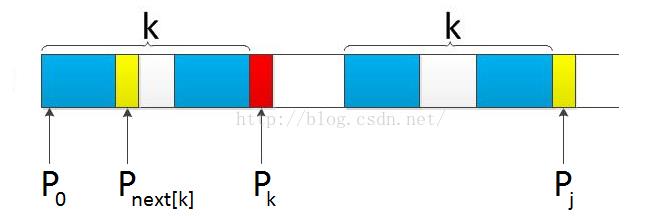
此过程相当于模式串的自我匹配，所以不断的递归k = next[k]，直到要么找到长度更短的同样前缀后缀。要么没有长度更短的同样前缀后缀。例如以下图所看到的： 

如今我们来測试下k回溯是不是能够找到之前同样前后缀：

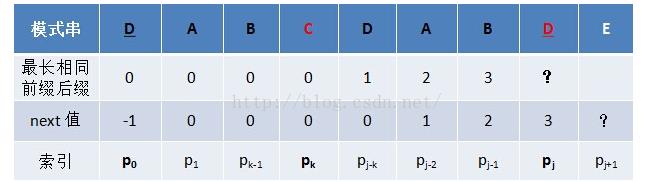
因为此时的C和D不匹配，所以k走到next[k]即k=0,此时p[0]=p[j]，所以next[j]=k+1=1。即字符E之前的字符串“DABCDABD”中有长度为1的同样前缀和后缀

此时我们最终大概明确了next数组的来历……也能自己敲出代码了，代码例如以下：

void GetNext(char* p,int next[])  
{  
    int pLen = strlen(p);  
    next[0] = -1;  
    int k = -1;  
    int j = 0;  
    while (j < pLen - 1){  
        //p[k]表示前缀，p[j]表示后缀  
        if (k == -1 || p[j] == p[k]){  
            ++k;  
            ++j;  
            next[j] = k;  
        }  
        else k = next[k];  
    }  
}  

当然。此时的KMP算法还是基础版。还有优化版见：
http://baike.baidu.com/link?url=7TyIFAuf53azP6XofEc5oWivGEp5Gt9Dxnmhy5USg7eyiZzEBWiBVLjle1ZpSBUMU-Zqgeh9qqPiQwRdN4lqEq中的优化部分。