中缀表达式转为后缀表达式

Posted 2020-10-03

首先我们想设计的表达式支持的数：整数(正整数，0，负整数)还有小数，注意了不仅仅只支持个位整数(之前做的都太局限了)

那么我们正常的表达式要做一下处理，让它能区分出操作符和操作数，方便我们更好的处理

想法：如果有东西能够隔开操作符和操作数就好了.。那行，那我们就用空格隔开吧

为什么要用空格？

因为有时候我们输入正常的表达式的时候会习惯性的按下空格，使用空格作为分隔，以后我们会将空格处理掉，也就无意的处理掉了习惯性而产生的问题。

那好我们直接上代码，里面有详细的注释

/**
     * 40开括号( 41闭括号) 42星号(乘号) 43加号 45减号 46句号(小数点) 47斜杠(除号) 48 数字0 57 数字9
     */
    public static void main(String[] args) {
        String str = "(2+3.2)+Math.ceil(4)*(409-56+(-136/5)*9)";
        StringBuilder sb = new StringBuilder();
        char lastC = 0;
        char c = 0;
        for (int i = 0; i < str.length(); i++) {
            c = str.charAt(i);
            if (c > 57 || c < 48) {// 非数字
                if (c == 46 && lastC <= 57 && lastC >= 48) {// 小数点       如果c为小数点，并且lastC为数字，那就直接append到sb里面
                    sb.append(c);
                } else if (lastC == 40 && c == 45) {// 负数   如果lastC为左括号，c为减号或者负号(减号)，那就直接append到sb里面
                    sb.append(c);
                } else if (c == 40 || c == 41 || c == 42 || c == 43 || c == 45
                        || c == 47) {//如果是左括号 右括号 乘号 加号 减号 除号 则空格隔开，在append到sb里面
                    sb.append(" ").append(c).append(" ");
                }else{//其他字符直接append到sb里面
                    sb.append(c);
                }
            } else {// 数字 是数字就直接append到sb里面
                sb.append(c);
            }//记录上一个字符
            lastC = c;
        }
        System.out.println(sb.toString());
    }

运行结果：

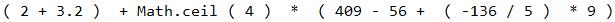
这个表达式(2+3.2)+Math.ceil(4)*(409-56+(-136/5)*9)几乎涵括了所有的可能性，大家先忽略Math.ceil这个字符串，这是在下一篇用到了，为了是我们的表达式更加的丰富。

那好，我们回归正题，如何将正常的表达式写出逆波兰表达式呢？

思路：

　　①我们用一个相同容量的数组strs来存储关于逆波兰表达式的字符串，最终将会变成逆波兰表达式，用一个栈stack s来保存操作符

　　②从左到右遍历字符串数组

　　③当遇到操作数时，直接存储到数组strs里面

　　④当遇到操作符是，就要比较其与栈顶的优先级

　　　　1、当栈stack为空，或栈顶运算符为左括号“(”，则直接将此操作符入栈；

　　　　2、否则，若优先级比栈顶运算符的高，也将操作符压入S1

　　　　3、否则，将stack栈顶的运算符弹出并存储到strs数组中，再次转到(③-1)与stack中新的栈顶运算符相比较；

 

　　⑤遇到括号：

　　　　1、当遇到左括号"{"时，将它压入栈里面

　　　　2、当遇到右括号")"时，依次弹出操作符并且添加到sb里面，直到遇到左括号“(”，此时左右括号都作废

　　⑥重复②~⑤的步骤

　　⑦当遍历结束后，将栈里面剩余的操作符依次弹出并且添加到数组strs里面

例如

(2+3.2)+4*(40-5+(-1)*4)    -------->  2 3.2 + 4 40 5 - -1 4 * + * +

 ( 2 + 3.2 )  + 4 *  ( 40 - 5 +  ( -1 )  * 4 )      ---------转换为数组--------->     [(, 2, +, 3.2, ), +, 4, *, (, 40, -, 5, +, (, -1, ), *, 4, )]

遍历到的字符串：str

存储关于逆波兰字符串的数组：strs

存储操作符的stack

　         str　　                               strs            　        　　       stack　　　　　　　　理由

　  　　(　　　　　　　　　　　  空　　　　　　　　　　　　(　　　　　　左括号，压入栈中

　　　  2　　　　　　　　   　　  ["2"]　　　　　　　　　　　(　　　　　　数字，直接存储到数组strs里面　

　　　  +　　　　　　　　  　　   ["2"]　　　　　　　　　　  ( +　　　　　  操作符压入栈中

　　　  3.2　　　　　　　　　   ["2","3.2"]　　　　　　　　　( +　　　　　  数字，直接存储到数组strs里面

　　     )　　　　　　　　　　 ["2,"3.2","+"]　　　　　　　　　空　　　　　 右括号，将操作符依次弹出，直到左括号，这时左括号已经弹出，stack空

　　　 +         　　　　　　　  ["2,"3.2","+"]　　　　　　　　　+　　　　　　stack为空，直接压入栈

　　　 4         　　　　　　  ["2,"3.2","+","4"]　　　　　　　　  +                     操作数，直接存储到strs里面

　　　 *         　　　　　　  ["2,"3.2","+","4"]　　　　　　　　 + *　　　　　 操作符*号比栈顶的+号高，将*压入栈

　　     (        　　　　　　   ["2,"3.2","+","4"]　　　　　　　　+ * (　　　　   左括号直接压入栈顶

　　　 40　　　　　　　 ["2,"3.2","+","4","40"]　　　　　　　+ * (　　　　　数字，直接存储到数组strs里面

　　　 -　　　　　　　　["2,"3.2","+","4","40"]　　　　　　　+ * ( -　　　　  栈顶为左括号，操作符直接压入栈

　　    5　　　　　　　　["2,"3.2","+","4","40","5"]　　　　　  + * ( -　　　　 数字，直接存储到数组strs里面

　　　+　　　　　　     ["2,"3.2","+","4","40","5","-"]　　　　   + * ( +　　　　操作符+号并没有比操作符-号优先，所以将-号弹出，在跟新的栈顶比较

　　　(　　　　　　      ["2,"3.2","+","4","40","5","-"]　　　     + * ( + (　　　　左括号直接压入栈顶

　　　-1　　　　　   ["2,"3.2","+","4","40","5","-","-1"]　　　   + * ( + (　　　　数字，直接存储到数组strs里面

　　　)　　　　　　 ["2,"3.2","+","4","40","5","-","-1"]　　　　 + * ( +　　　　 遇到了右括号，依次弹出，直到遇到左括号

　　    *　　　　　　 ["2,"3.2","+","4","40","5","-","-1"]　　　　+ * ( + *　　　 操作符*号的优先级比操作符+号高，直接压入栈

　　    4　　　　　["2,"3.2","+","4","40","5","-","-1","4"]　　　  + * ( + *　　　 数字，直接存储到数组strs里面

　　　)　　　　　["2,"3.2","+","4","40","5","-","-1","4","*","+"]      + *　　　　   右括号，依次弹出，直到遇到左括号

　　最后　　　["2,"3.2","+","4","40","5","-","-1","4","*","+","*","+"]  空　　　　　依次弹出栈里面的操作符，直到为空

那么我们最后得到的数组["2,"3.2","+","4","40","5","-","-1","4","*","+","*","+"] 是不是跟我们要的逆波兰表达式2 3.2 + 4 40 5 - -1 4 * + * +完全一样

那么接下来，上代码

// (2+3.2)+4*(40-5+(-1)*4)
    static String strs[] = { "(", "2", "+", "3.2", ")", "+", "4", "*", "(",
            "40", "-", "5", "+", "(", "-1", ")", "*", "4", ")" };// 正常的表达式经过上面的处理，变成了这样的数组
    static String strsBo[] = new String[strs.length];// 存储关于逆波兰的字符串数组
    static int index = 0;// strsBo的下一个存储下标，从0开始
    static Stack<String> stack = new Stack<>();// 存储操作符的栈

    public static void main(String[] args) {
        for (String str : strs) {
            if (str.matches("-?[0-9]+") || str.matches("-?[0-9]+.?[0-9]+")) {// 判断是否是数值
                strsBo[index++] = str;
            } else {
                handleStack(str);
            }
        }
        // 当遍历结束后，将栈里面剩余的操作符依次弹出并且添加到数组strs里面
        while (stack != null && !stack.empty()) {
            strsBo[index++] = stack.pop();
        }
        System.out.println(Arrays.toString(strsBo));
    }

    private static void handleStack(String str) {
        if (str.equals("(")) {// 当遇到左括号"("时，将它压入栈里面
            stack.push(str);
        } else if (str.equals(")")) {// 遇到了右括号,依次弹出操作符并且添加到strsBo里面，直到遇到左括号“(”，此时左右括号都作废
            String pop = stack.pop();
            while (!pop.equals("(")) {
                strsBo[index++] = pop;
                pop = stack.pop();
            }
        } else if (stack.isEmpty() || stack.lastElement().equals("(")) {// 栈stack为空，或栈顶运算符为左括号“(”，则直接将此操作符入栈
            stack.push(str);
        } else {// 操作符不为右括号，才比较优先级
            if (priority(str, stack.lastElement())) {// 若优先级比栈顶运算符的高，也将操作符压入stack
                stack.push(str);
            } else {// 否则，将stack栈顶的运算符弹出并存储到strs数组中，再次与stack中新的栈顶运算符相比较
                strsBo[index++] = stack.pop();
                handleStack(str);
            }
        }
    }

    /**
     * @return 只有str1的优先级高于str2的优先级才返回false
     *         ,只有一种情况才返回true，那就是str1为乘除，str2为加减，其他情况都为false
     */
    public static boolean priority(String str1, String str2) {
        return (str1.equals("*") || str1.equals("/"))
                && (str2.equals("+") || str2.equals("/"));
    }

运行结果：

没问题，跟我们要的结果一样。下一篇将会用面向对象的思想来将他们封装一下，是他们更容易的扩展。