51nod 1270 数组的最大代价 思路：简单动态规划

Posted 2020-10-03

 

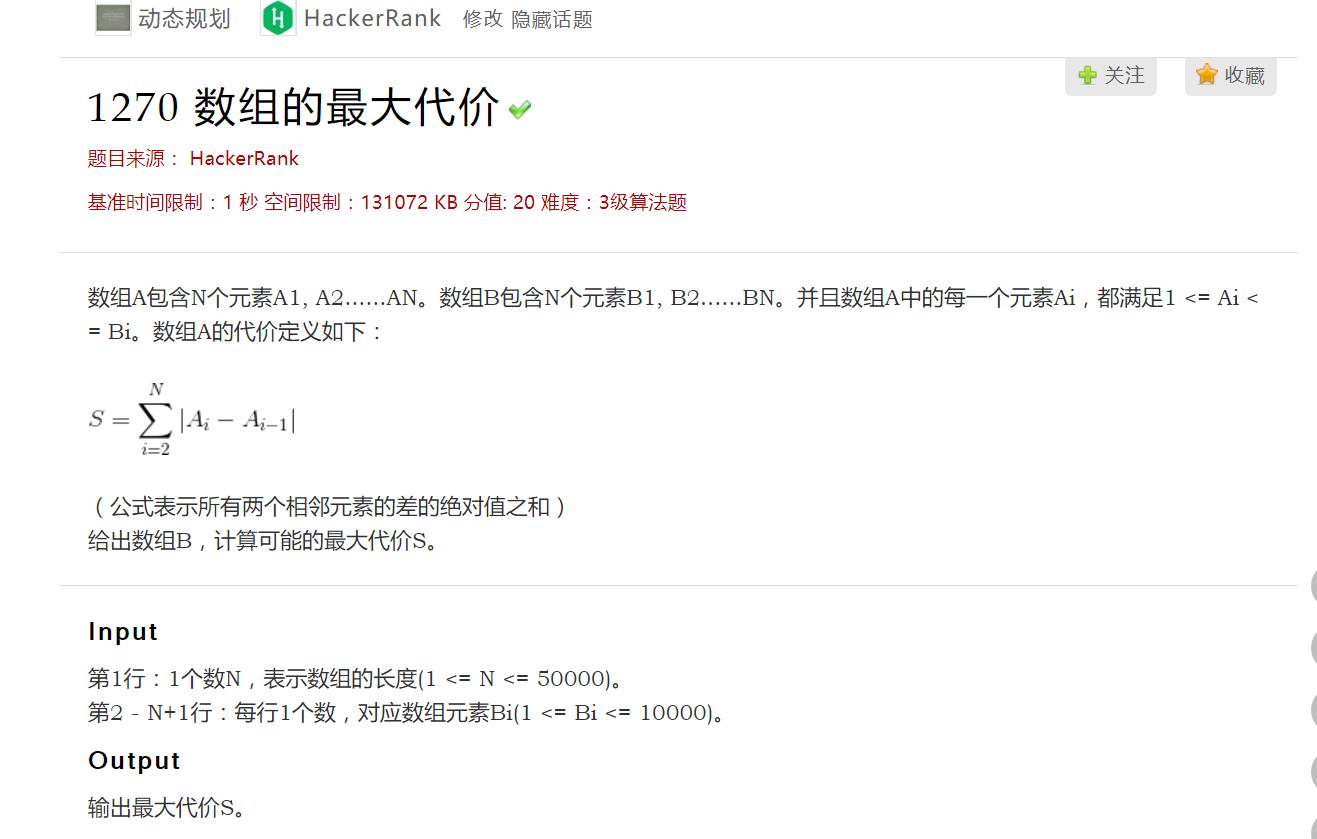
这题是看起来很复杂，但是换个思路就简单了的题目。

 

首先每个点要么取b[i]，要么取1,因为取中间值毫无意义，不能增加最大代价S。

用一个二维数组做动态规划就很简单了。

 

dp[i][0]表示第i个点取1时（第0-i个点）得到的最大代价之和。

dp[i][1]表示第i个点取b[i]时（第0-i个点）得到的最大代价之和。

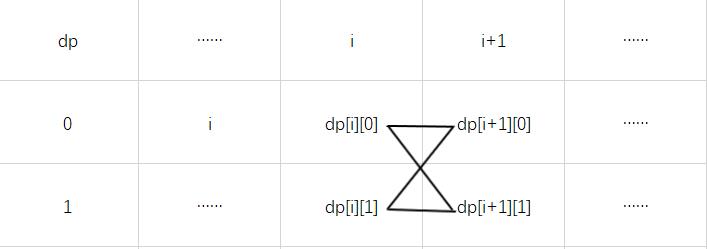
每一个都由前面两个推出。

 

#include <bits\\stdc++.h>
using namespace std;


int a[50005];
int dp[50005][2]; // dp[][0]表示取1，dp[][1]表示取a[i] 
int main(){
    int n;
    cin >> n;
    for(int i = 0;i < n; i++){
        cin >> a[i];
    }

    for(int i = 1;i < n; i++){
        dp[i][0] = max(abs(1-1)+dp[i-1][0],    // 第i个为1 ，第i-1个为1 
                            abs(1-a[i-1])+dp[i-1][1]);   // 第i个为1 ，第i-1个为a[i-1] 
        dp[i][1] = max(abs(a[i]-1)+dp[i-1][0], // 第i个为a[i] ，第i-1个为1 
                            abs(a[i]-a[i-1])+dp[i-1][1]);// 第i个为a[i] ，第i-1个为a[i-1] 
    }
//    for(int i = 0;i < n; i++){
//        cout << dp[i][0] << " " << dp[i][1] << endl; 
//    } 
    cout << max(dp[n-1][0],dp[n-1][1]) << endl; //答案为最后一组中的最大的那个 
    return 0;
}