http://codeforces.com/problemset/problem/712/D

Posted 2020-10-03 lhclqslove

D. Memory and Scores

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Memory and his friend Lexa are competing to get higher score in one popular computer game. Memory starts with score a and Lexa starts with score b. In a single turn, both Memory and Lexa get some integer in the range [ - k;k] (i.e. one integer among  - k,  - k + 1,  - k + 2, ...,  - 2,  - 1, 0, 1, 2, ..., k - 1, k) and add them to their current scores. The game has exactly t turns. Memory and Lexa, however, are not good at this game, so they both always get a random integer at their turn.

Memory wonders how many possible games exist such that he ends with a strictly higher score than Lexa. Two games are considered to be different if in at least one turn at least one player gets different score. There are (2k + 1)2t games in total. Since the answer can be very large, you should print it modulo 109 + 7. Please solve this problem for Memory.

Input

The first and only line of input contains the four integers a, b, k, and t (1 ≤ a, b ≤ 100, 1 ≤ k ≤ 1000, 1 ≤ t ≤ 100) — the amount Memory and Lexa start with, the number k, and the number of turns respectively.

Output

Print the number of possible games satisfying the conditions modulo 1 000 000 007 (109 + 7) in one line.

Examples

input

1 2 2 1

output

6

input

1 1 1 2

output

31

input

2 12 3 1

output

0

Note

In the first sample test, Memory starts with 1 and Lexa starts with 2. If Lexa picks  - 2, Memory can pick 0, 1, or 2 to win. If Lexa picks - 1, Memory can pick 1 or 2 to win. If Lexa picks 0, Memory can pick 2 to win. If Lexa picks 1 or 2, Memory cannot win. Thus, there are3 + 2 + 1 = 6 possible games in which Memory wins.

 题意：两个人最开始有a,b两个初始数，玩t轮游戏，每个人都随机从【-k,k】之间获得一个数加进他们的分数，问最后问最开始是a的人比另外一个大的方案数%1e9就可以；

题解：f[i]表示得分为i的情况数（每轮更新），然后用sum[]来维护f[i]的前缀和，状态转移方程就是f[j]=(sum[loc]-sum[j-k-1]+mod)%mod;（loc=min(j+k,r-k)注意边界）

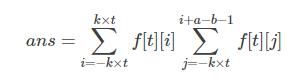
然后就是数组下表不能小于0；

#include<iostream>
#include<cstdio> 
#include<cstring>
#include<cmath> 
#include<algorithm> 
#define ll long long
double eps=1e-7; 
const int maxn=4e5+2000; 
int zero=2e5+2005; 
const int mod=1e9+7; 
using namespace std;
int f[maxn],sum[maxn]; 
int a,b,k,t; 
int main()
{
    scanf("%d %d %d %d",&a,&b,&k,&t);
    int l=zero-k,r=zero+k; 
    //if(a==1&&b==100&&k==1000&&t==100) 
    for(int i=l;i<=r;i++)
    {
        f[i]=1;
        sum[i]=sum[i-1]+f[i]; 
    } 
    for(int i=2;i<=t;i++)
    {
         l=zero-k*i,r=zero+k*i;
         for(int j=l;j<=r;j++)
         {
             int loc=min(j+k,r-k);
             f[j]=(sum[loc]-sum[j-k-1]+mod)%mod; 
         }
         for(int j=l;j<=r;j++)
         {
             sum[j]=(sum[j-1]+f[j])%mod; 
         } 
    } 
     l=zero-t*k; r=zero+t*k; 
     int ans=0; 
    for(int i=l;i<=r;i++)
    {
        int loc=min(i+a-b-1,r); 
        ans=(ans+((ll)sum[loc]*f[i])%mod)%mod; 
    } 
    printf("%d\\n",ans); 
     
}