数学中几种经常使用的距离

Posted 2020-10-03 lxjshuju

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数学中几种经常使用的距离相关的知识，希望对你有一定的参考价值。

数学中有非常多不同种类的距离，经常使用于几何、高等代数等数学研究。

多种多样的距离在数学建模、计算机学习中有着不小的应用。

比方，A*搜索时的评估函数。

比方，在机器学习中，做分类时经常须要估算不相同本之间的类似性度量(Similarity Measurement)。这时通常採用的方法就是计算样本间的距离。採用什么样的方法计算距离是非常讲究。甚至关系到分类的正确与否。

欧氏距离(Euclidean Distance)

欧氏距离是最易于理解的一种距离计算方法，源自欧几里得几何中两点间的距离公式。

(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离：

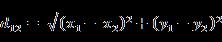
(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离：

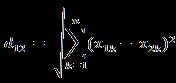
也能够用表示成向量运算的形式：

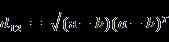
(4)Matlab计算欧氏距离

Matlab计算距离主要使用pdist函数。

若X是一个M×N的矩阵。则pdist(X)将X矩阵M行的每一行作为一个N维向量。然后计算这M个向量两两间的距离。

样例：计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离

X = [0 0 ; 1 0 ; 0 2]

D = pdist(X,\'euclidean\') %大家能够去查一查pdist的參数

结果：

D =

    1.0000    2.0000    2.2361

从名字就能够猜出这样的距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。

实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离(City Block distance)。

(1)二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离

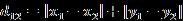
(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离

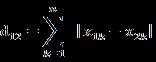
(3) Matlab计算曼哈顿距离

样例：计算向量(0,0)、(1,0)、(0,2)、(2,2)两两间的曼哈顿距离

X = [0 0 ; 1 0 ; 0 2 ; 2 2];

D = pdist(X,\'cityblock\')

结果：

D =

     1     2     4     3     3     2

国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的随意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少须要多少步？自己走走试试。

你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步。有一种类似的一种距离度量方法叫切比雪夫距离。

(1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离

(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离

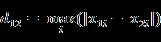
　　这个公式的还有一种等价形式是

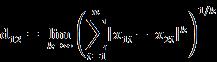
看不出两个公式是等价的？提示一下：试试用放缩法和夹逼法则来证明。

(3)Matlab计算切比雪夫距离

样例：计算向量(0,0)、(1,0)、(0,2)两两间的切比雪夫距离

X = [0 0 ; 1 0 ; 0 2]

D = pdist(X, \'chebychev\')

结果：

D =

     1     2     2

闵氏距离不是一种距离。而是一组距离的定义，上文说的几个距离都是属于闵可夫斯基距离的。

(1) 闵氏距离的定义

两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,SQL Server中几种遍历方式比较