最短路径算法-Dijkstra

Posted 2020-06-28 泡面狂

Dijkstra是解决单源最短路径的一般方法，属于一种贪婪算法。

所谓单源最短路径是指在一个赋权有向图中，从某一点出发，到另一点的最短路径。

 

以python代码为例，实现Dijkstra算法

1、数据结构设计

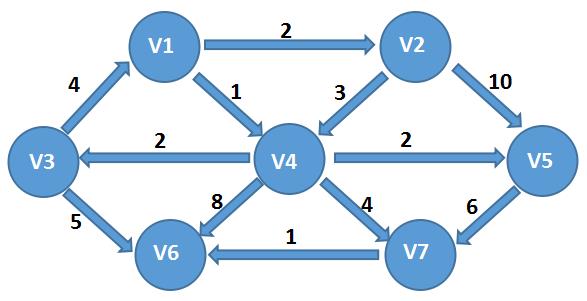
假设图以单边列表的方式进行输入，本例使用如下的一个图来进行分析：

E = ((1,2,2),
(1,4,1),
(2,4,3),
(2,5,10),
(3,1,4),
(3,6,5),
(4,3,2),
(4,6,8),
(4,7,4),
(4,5,2),
(5,7,6),
(7,6,1))

E表示一个图，它是一个二维列表，三个一组表示一条边，三个值分别为边的起点、终点，以及该边的权值。

上面这个边列表表示的图如下：

只设计一个顶点结构就OK了，顶点的表示如下：

class V_NODE(object):
    def __init__(self, id):
        self.id = id
        self.adja_list = 0
        self.path = 0
        self.kown = False
        self.dist = float("inf")

id表示顶点的编号；

path表示到该顶点对应的最优路径的上一个顶点；

kown用来记录改点的最短路径是否已经找到；

dist表示改点当前路径的长度；

adja_list用来存放改顶点的邻接点的列表，采用二维列表，每个元组有两个值：与改点相邻的点的id、到该点的路径的长度

 

2、算法实现

def read_graph(edge):
    hash = {}
    for e in edge:
        if hash.has_key(e[0]):
            hash[e[0]].adja_list.append([e[1],e[2]])
        else:
            v = V_NODE(e[0])
            v.adja_list=[[e[1],e[2]]]
            hash[e[0]] = v
        if hash.has_key(e[1]) == False:
            v = V_NODE(e[1])
            v.adja_list=[]
            hash[e[1]] = v
    return hash

def find_best_unkown(hash_unkown):
    dist = float("inf")
    id = -1
    for k in hash_unkown.keys():
        if dist > hash_unkown[k].dist:
            dist = hash_unkown[k].dist
            id = k
    return id

def print_path(hash_kown, v1, v2):
    b_str = "%d to %d: " % (v1,v2)
    if hash_kown.has_key(v2) == False :
        print b_str + "no way form %d to %d" % (v1, v2)
        return
    
    str = ""
    while v2 != v1:
        str = "->%d" % v2 + str
        v2 = hash_kown[v2].path
    str = "%d" % v2 + str
    print b_str + str
    
def find_best(edges, v1, v2):
    hash_unkown = read_graph(edges)
    hash_unkown[v1].dist = 0
    hash_unkown[v1].path = v1
    hash_kown = {}
    while 1:
        v_id = find_best_unkown(hash_unkown)
        #print "best: %d" % v_id
        if v_id < 0 :
            break
        hash_unkown[v_id].kown = True
        hash_kown[v_id] = hash_unkown[v_id]
        del hash_unkown[v_id]
        for w in hash_kown[v_id].adja_list:
            if hash_unkown.has_key(w[0]):
                if hash_kown[v_id].dist + w[1] < hash_unkown[w[0]].dist:
                    hash_unkown[w[0]].dist = hash_kown[v_id].dist + w[1]
                    hash_unkown[w[0]].path = v_id
    
    #for k in hash_kown.keys():
    #    hash_kown[k].show()

    print_path(hash_kown,v1,v2)


# for test...
for i in range(1,8):
    for j in range(1,8):
        find_best(E, i, j)

首先实现函数read_graph，它读入一个以单边列表表示的图，输出一个带有邻接表的顶点哈希表；

然后实现函数find_best_unkown，它在未知顶点中寻找距源点路径最短的一个顶点并返回其id；

print_path函数用来打印出某个指定顶点的路径信息；

最终实现find_best函数，它接收一个图的单边列表，以及源点v1和终点v2，然后计算并打印出v1到v2的最短路径。

最后还有个for循环用来测试，将任意两点间的最优路径都计算出来。