655. Print Binary Tree 解题报告（树）

Posted 2020-10-02

第一部分：搜索、遍历

 【例子1】655. Print Binary Tree

Example 1:

Input:
     1
    /
   2
Output:
[["", "1", ""],
 ["2", "", ""]]

 

Example 2:

Input:
     1
    /    2   3
         4
Output:
[["", "", "", "1", "", "", ""],
 ["", "2", "", "", "", "3", ""],
 ["", "", "4", "", "", "", ""]]

思路：先求高度，初始化数组，然后DFS递归即可。在DFS时，需要注意确定左右边界。

代码：

vector<vector<string>> printTree(TreeNode* r) {
        int d = hight(r);
        vector<vector<string>> res(d,vector<string>(pow(2,d)-1,""));
        DFS(r,0,res,0,res[0].size()-1);
        return res;
    }
    
    int hight(TreeNode* r){
        if(!r)return 0;
        return max(hight(r->left),hight(r->right))+1;
    }
    
    void DFS(TreeNode* root,int d,vector<vector<string>>& res, int L, int r ){
        int mid = (L+r)/2;
        res[d][mid] = to_string(root->val);
        if(root->left)DFS(root->left,d+1,res,L,mid-1);
        if(root->right)DFS(root->right,d+1,res,mid+1,r);
    }

View Code

 

【例子2】366. Find Leaves of Binary Tree

Given a binary tree, collect a tree‘s nodes as if you were doing this: Collect and remove all leaves, repeat until the tree is empty.

Example:
Given binary tree 

          1
         /         2   3
       / \\     
      4   5    

 

Returns [4, 5, 3], [2], [1].

思路：我最开始的思路是求出每一个节点的depth，并且给res[depth]添加当前节点的val。如果是第一次遇到这样的深度，这时候给res中添加vector，再添加当前节点的val。换句话说，我们是在用DFS求高度的同时向res中添加各个高度的节点val。另外，还有一种不断删除叶子节点的递归方法。

代码：

DFS求高度

DFS不断减除叶子节点

【例子3】515. Find Largest Value in Each Tree Row

You need to find the largest value in each row of a binary tree.

Example:

Input: 

          1
         /         3   2
       / \\   \\  
      5   3   9 

Output: [1, 3, 9]

思路：这个问题既可以用BFS，也可以用DFS（res,depth,root）。

代码：

DFS

    vector<int> largestValues(TreeNode* root) {
        vector<int> res;
        DFS(res,root,0);
        return res;
    }
    
   void DFS(vector<int>& res,TreeNode* r, int d){
       if(r==NULL)return;
       if(res.size()<=d)res.push_back(r->val);
       else res[d] = max(res[d],r->val);
       DFS(res,r->left,d+1);
       DFS(res,r->right,d+1);
   }

【例子4】563. Binary Tree Tilt

Given a binary tree, return the tilt of the whole tree.

The tilt of a tree node is defined as the absolute difference between the sum of all left subtree node values and the sum of all right subtree node values. Null node has tilt 0.

The tilt of the whole tree is defined as the sum of all nodes‘ tilt.

Example:

Input: 
         1
       /         2     3
Output: 1
Explanation: 
Tilt of node 2 : 0
Tilt of node 3 : 0
Tilt of node 1 : |2-3| = 1
Tilt of binary tree : 0 + 0 + 1 = 1

 思路：递归，最开始的做法是用root的Tilt再加上左右两个子树的Tilt，root的Tilt再用sum(r->left) - sum(r->right)得到。这种做法每个节点都至少遍历了两次。有一种更加高效的递归方法，在求子树和的同时，就可以顺便将左右子树之差加到ans上面，经过递归，就能够得到各个节点左右子树之差的和。

代码：

 int findTilt(TreeNode* root) {
        if(!root)return 0;
        int sum=0;
        helper(root,sum);
        return sum;
    }
    
    int helper(TreeNode* r,int& sum){
        if(!r)return 0;
        int L = helper(r->left,sum),R = helper(r->right,sum);
        sum += abs(L-R);
        return r->val + L + R;
    }

View Code

【例子5】 sum of all left leaves

Find the sum of all left leaves in a given binary tree.

Example:

    3
   /   9  20
    /     15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

思路：递归，设立标志（向左or向右），引用传递，所以递归函数一共有三个参数，见代码。我最开始的思路，没有想到设立方向标志，从而在判断某一节点的左节点是否为左叶子节点时，耗费不少时间。

代码：

 int sumOfLeftLeaves(TreeNode* root) {
        int sum = 0;
        helper(root,sum,false);
        return sum;
    }
    
    void helper(TreeNode* root, int& sum,bool isLeft){
        if(!root){
            return;
        }else if(isLeft&&!root->left&&!root->right){
            sum += root->val;
            return;
        }else{
            helper(root->left,sum,true);
            helper(root->right,sum,false);
        }
       
    }

View Code

 【例子6】103. Binary Tree Zigzag Level Order Traversal

Given a binary tree, return the zigzag level order traversal of its nodes‘ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

    3
   /   9  20
    /     15   7

 

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

思路：层序遍历的变种，只要考虑轮流着采用不同的顺序放到当前的vector数组中即可。添加来l2r（left to right ）bool变量，表面当前的方向。

代码：

vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int> > res;
        if(!root) return res;
        queue<TreeNode*> q;
        q.push(root);
        bool l2r = true;
        int size = 1;
        while (size!=0) {
            vector<int> cur(size);
            for (int i = 0; i < size; i++) {
                TreeNode *t = q.front();
                q.pop();
                
                int index = l2r ? i : (size - 1 - i);
                cur[index] = t->val;
                if(t->left)q.push(t->left);
                if(t->right)q.push(t->right);
            }
            res.push_back(cur);
            l2r = !l2r;
            size = q.size();
        }
        return res;
    }

View Code

 【例子7】106. Construct Binary Tree from Inorder and Postorder Traversal

思路：最开始写的递归程序中，包括两个数组的左、右索引，再加上两个数组，一共有6个参数。看了别人的代码，发现递归函数可以更简单，每次都将postorder中未访问的最后一个元素作为根节点，index最初等于post.size()-1，找到以这个位置为根节点的其他节点的范围（start，end），每次递归之后过后index--。另外，还可以添加一个hashmap，一次性写入inorder中各个元素的位置。总之，设置函数参数时，需要考虑参数之间的相关性。

代码：

 TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {
        if(inorder.empty()||postorder.empty())return NULL;
        int start = 0, end = inorder.size()-1, index = end;
        return buildTree(inorder, postorder, start, end, index);
    }
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder, int start, int end, int& index) {
        int key = postorder[index],i = start;
        TreeNode *cur = new TreeNode(key);
        while(inorder[i]!=key)i++;
        if(i<end)cur->right = buildTree(inorder, postorder,i+1, end,--index);
        if(i>start)cur->left = buildTree(inorder, postorder, start, i-1,--index);
        return cur;
    }

View Code

 

 

第二部分：BST

【例子1】98. Validate Binary Search Tree

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node‘s key.
• The right subtree of a node contains only nodes with keys greater than the node‘s key.
• Both the left and right subtrees must also be binary search trees.

思路：

思路一：利用递归，我最开始写的递归只有一个TreeNode参数，边界判断用max和min函数求某一根节点的最右边子节点和最左子节点。其实，更好的做法是在递归函数的参数中加上max和min，在递归的同时更新max和min状态。这里把别人的代码搬过来了，连接：https://discuss.leetcode.com/topic/7179/my-simple-java-solution-in-3-lines。

思路二：上面的思路中，在初始化max和min非常关键，例如，在C++中，如果max=INT_MAX,这是行不通的，有的节点val刚好就是这个值，所以要选比INT_MAX还要大的数字。第二种思路就没有上述困惑，选择添加一个前驱节点，再按照中序遍历二叉树，如果pre->val>= cur->val，就说明不是BST。

代码：

添加最大最小边界

    bool isValidBST(TreeNode* root) {
        TreeNode *pre = NULL;
        return helper(root,pre);
    }
    
    bool helper(TreeNode *r,TreeNode* &pre){
        if(!r)return true;
        if(!helper(r->left,pre))return false;
        if(pre!=NULL&&pre->val>=r->val)return false;
        pre = r;
        return helper(r->right,pre);
    }

添加前驱节点

【例子2】95. Unique Binary Search Trees II

Given an integer n, generate all structurally unique BST‘s (binary search trees) that store values 1...n.

For example,
Given n = 3, your program should return all 5 unique BST‘s shown below.

   1         3     3      2      1
    \\       /     /      / \\           3     2     1      1   3      2
    /     /       \\                    2     1         2                 3

思路1：递归，由于这里BST左子树节点的val一定小于root，右子树节点的val一定大于root，所以，可以单独把1到n中的一个数字i作为root->val，这时候，1到i-1就建立左子树，i+1到n就建立右子树，用递归函数调用即可。

思路2：动态规划，根据上面的递归思想，可以设置一个二维的dp数组，dp[i][j]表示从i到j所有BST，即一个vector<TreeNode*>，从而有dp[i][j] = sum（dp[i][k-1]-root(k) - dp[k+1][j]），k为i和j之间的一个数字，表示把k作为BST的root。最后，我们得到dp[1][n]即可。

代码：

递归

vector<TreeNode*> generateTrees(int n) {
        if(n==0)return vector<TreeNode*>();
        vector<vector<vector<TreeNode*>>> dp(n+2, vector<vector<TreeNode*>>(n+2, vector<TreeNode*>(0)));
        //考虑到以n为根节点时，右边dp[n+1][n]需要时NULL，所以这里dp数组的长度应该是n+2。
        for(int i=1;i<=n+1;i++){
            for(int j=0;j<i;j++){
                dp[i][j].push_back(NULL);
            }
        }
        for(int i=n;i>=1;i--){
            for(int j=i; j<=n;j++){
                for(int k=i;k<=j;k++){
                    for(auto lt:dp[i][k-1]){
                        for(auto rt:dp[k+1][j]){
                            TreeNode* r = new TreeNode(k);
                            r->left = lt;
                            r->right = rt;
                            dp[i][j].push_back(r);
                        }
                    }
                    
                }
            }
        }
        return dp[1][n];
    }

动态规划

【例子3】99. Recover Binary Search Tree

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

思路1：最开始我是用分治法。因为交换了BST中的两个元素，所以，可以得到，BST一定可以分成左右两部分，左边部分的最大值要大于右边部分的最小值。例如，左右子树交换节点之后，左边子树的最大值必定是交换来的元素，而右边子树的最小值同样如此。于是，就可以先看看左边子树的最大值是否小于右边子树的最小值，如果不是，则已经找到交换的节点，否则，就说明左子树中交换了节点， 或者右子树中交换了节点，再对这两个子树分别进行递归就行了。然而，再编码的时候，还需要考虑到交换的刚好是root和root->left这种情况，所以，我们在求最大最小值都应该把root考虑进去。例如：【1,0】，左子树为空，求得max(null,1) = 1，右子树是0，求得min(1,0) = 0.

由于T(n) = 2T(n/2) + n，时间复杂是是：o(nlgn)

思路2：直接利用中序遍历找到两个异常节点，再交换它们的val即可。这个思路简单易懂，同时也只需要遍历一次BST。

代码：

分治法

public void recoverTree(TreeNode root) {
        if(root==null)return;
        boolean isMax = true,isMin=false;
        TreeNode first = root,second = root;
        //拿左子树的最大节点和root比较    
        if(root.left!=null){
            TreeNode temp = find(root.left,isMax);
            first = first.val>temp.val?first:temp;
        }
        ////拿右子树的最小节点和root比较   
        if(root.right!=null){
            TreeNode temp = find(root.right,isMin);
            second = second.val<temp.val?second:temp;
        }
       //没有找到，两边就都是root，所以val相等
        if(first.val==second.val){
            recoverTree(root.left);
            recoverTree(root.right);
        }
        else{
            int t = first.val;
            first.val =second.val;
            second.val = t;
        }
    }
    
    public TreeNode find(TreeNode root,boolean isMax){
        if(root==null)return null;
        TreeNode ans = root;
        if(root.left!=null){
            TreeNode l=find(root.left,isMax);
            ans = isMax ? (l.val>ans.val?l:ans) : (l.val>ans.val?ans:l);
        }
        if(root.right!=null){
            TreeNode r=find(root.right,isMax);
            ans = isMax ? (r.val>ans.val?r:ans) : (r.val>ans.val?ans:r);
        }
        return ans;
    }    

 TreeNode* first, *second, *pre = new TreeNode(INT_MIN);
    void recoverTree(TreeNode* root) {
        if(!root)return;
        inOrder(root);
        swap(first->val,second->val);
    }
    
    void inOrder(TreeNode* r){
        if(!r)return;
        inOrder(r->left);
        if(pre->val>r->val){
            if(!first){
                first = pre;//交换后，第一个节点必定大于它的后节点
            }
            second = r;
        }
        pre = r;
        inOrder(r->right);
    }

中序遍历

 

 

 

第三部分：路径求和与高度

 【例子1】124. Binary Tree Maximum Path Sum

Given a binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

For example:
Given the below binary tree,

       1
      /      2   3

 

Return 6.

思路：还是递归，注意必须包含一个节点，同时细分问题。最长路径和可以出现在左子树、右子树、经过顶点的路径（新的递归函数）。这里需要注意，经过顶点的最大和路径时，先求出在左节点结束的最大路径和，在右边节点结束的最大路径和，看看它们是否大于0，如果大于就再加上root->val，从而得到最终的经过顶点的最大路径和。这里depth（root)表示以该点结束的最大路径和,递归函数和求高度很相似。

代码：

 int maxPathSum(TreeNode* root) {
        int temp1 = 0,temp2=0,temp3=INT_MIN;
        if(root->left){
            temp1 = max(depth(root->left),temp1);
            temp3 = max(maxPathSum(root->left),temp3);
        }
        if(root->right){
            temp2 = max(depth(root->right),temp2);
            temp3 = max(maxPathSum(root->right),temp3);
        }
        return max(temp3,root->val + temp1 + temp2);
    }
    
    int depth(TreeNode* root){
        int temp1 = 0,temp2=0;
        if(root->left)temp1 = max(depth(root->left),temp1);
        if(root->right)temp2 = max(depth(root->right),temp2); 
        return max(temp1,temp2) + root->val;
    }

View Code

 【例子2】508. Most Frequent Subtree Sum

Given the root of a tree, you are asked to find the most frequent subtree sum. The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself). So what is the most frequent subtree sum value? If there is a tie, return all the values with the highest frequency in any order.

Examples 1
Input:

  5
 /  2   -3

return [2, -3, 4], since all the values happen only once, return all of them in any order.

思路：显然，一个节点为只能是一棵子树的根节点。这里就可以用递归的方法求出每一棵子树的sum，然后用hashtmap存下来即可。

代码：

vector<int> findFrequentTreeSum(TreeNode* root) {
        int maxcnt = 0;
        unordered_map<int,int> cnt;
        sum(root,cnt, maxcnt);
        vector<int> res;
        for(auto s: cnt){
            if(s.second==maxcnt)res.push_back(s.first);
        }
        return res;
    }
    
    int sum(TreeNode* r, unordered_map<int,int>& cnt,int& maxcnt){
        if(!r)return 0;
        int ans =  sum(r->left,cnt,maxcnt)+r->val + sum(r->right,cnt,maxcnt);
        cnt[ans]++;
        maxcnt = max(cnt[ans],maxcnt);
        return ans;
    }

View Code

【例子3】538. Convert BST to Greater Tree

Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.

Example:

Input: The root of a Binary Search Tree like this:
              5
            /              2     13

Output: The root of a Greater Tree like this:
             18
            /             20     13

思路：递归，为了不用全局变量，添加一个sum参数，表示之前的所有节点的和。

代码：

TreeNode* convertBST(TreeNode* root) {
        
        int sum = 0;
        helper(root,sum);
        return root;
        
    }
    
    void helper(TreeNode* root, int& sum){
         //结束标志
        if(root== NULL) return;
        //周期op和next()
        helper(root->right,sum);
        root->val += sum;
        sum = root->val;
        helper(root->left,sum);
    }

View Code

【例子4】116. Populating Next Right Pointers in Each Node

Given a binary tree

    struct TreeLinkNode {
      TreeLinkNode *left;
      TreeLinkNode *right;
      TreeLinkNode *next;
    }

 

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Note:

• You may only use constant extra space.
• You may assume that it is a perfect binary tree (ie, all leaves are at the same level, and every parent has two children).

 

For example,
Given the following perfect binary tree,

         1
       /        2    3
     / \\  /     4  5  6  7

 

After calling your function, the tree should look like:

         1 -> NULL
       /        2 -> 3 -> NULL
     / \\  /     4->5->6->7 -> NULL

思路：下一层的next指针可以由上一层推出，例如，cur->right->next = cur->next->left(5->6)。这里有几个关键变量，一个是每一层的开始节点，head，在上一层的循环中就要得到，另一个是连接连接时的尾节点tail，等找到该层下一节点时就让tail->next指向它，同时更新tail。cur则表示当前节点，cur=cur->next，如果遇到最后的空指针，就让cur=head，也就是下一层的开头节点。

代码：

void connect(TreeLinkNode *root) {
        if(!root)return;
        TreeLinkNode *head,*tail,*cur = root;
        head = tail = NULL;
        while(cur){
            if(cur->left){
                if(tail)tail = tail->next = cur->left;
                else head = tail = cur->left;
            }
            if(cur->right){
                if(tail)tail = tail->next = cur->right;
                else head = tail = cur->right;
            }
            cur = cur->next;
            if(!cur){
                cur = head;
                head = tail = NULL;
            }
        }
    }

View Code

【例子5】113. Path Sum II

Given a binary tree and a sum, find all root-to-leaf paths where each path‘s sum equals the given sum.

For example:
Given the below binary tree and sum = 22,

              5
             /             4   8
           /   /           11  13  4
         /  \\    /         7    2  5   1

return

[
   [5,4,11,2],
   [5,8,4,5]
]

思路：DFS，需要注意回溯的时机与返回的判断条件。

代码：

public List<List<Integer>> pathSum(TreeNode root, int sum) {
      List<List<Integer>> res=new ArrayList<List<Integer>>();
      if(root==null)return res;
      List<Integer> cur =new ArrayList<Integer>();
      op(res,cur,root,sum);
      return res;
    }
    
    private void op(List<List<Integer>> res,List<Integer> cur,TreeNode root,int sum){
        
        if(root.left==null&&root.right==null){
            if(sum==root.val){
                cur.add(root.val);
                res.add(new ArrayList<Integer>(cur));
                cur.remove(cur.size()-1);
                return;
            }else{
                return;
            }
        }
        cur.add(root.val);
        if(root.left!=null)op(res,cur,root.left,sum-root.val);
        if(root.right!=null)op(res,cur,root.right,sum-root.val);
        cur.remove(cur.size()-1);
    }

View Code

【例子6】110. Balanced Binary Tree

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

思路：最直观的做法是添加一个求高度的函数，判断左右子树的高度差，然后分治递归判断左右子树是否平衡。显然，这种方法浪费了时间，因为我们在求高度的时候就能够得到左右子树的高度差。

我最开始的方法，传递isBanlance引用，求出高度差，如果高度差大于1，则用这个变量记录下来。这样，在求到root的高度时，就已经得到是否为平衡树了。但是，这样的做法仍然做了些多余的工作，例如，即使我们已经知道不是平衡树了，但是，程序还在执行计算高度。

因此，优化的方法就是用返回的高度来代表这棵数是否平衡，如果求高度的时候遇到高度差大于1，就让节点高度为-1，并且返回。同样的，在求高度的时候，只要遇到高度为-1的节点，这时无需计算具体高度，都立即返回-1。

代码：

 bool isBalanced(TreeNode* root) {
        bool isB = true;
        high(root,isB);
        return isB;
    }
    
    int high(TreeNode *r,bool &isB){
        if(!r)return 0;
        int L = high(r->left,isB),R = high(r->right,isB);
        if(abs(L-R)>1)isB=false;
        return max(L,R)+1;
    }

未优化

 bool isBalanced(TreeNode* root) {
        return helper(root)!=-1;
    }
    
    int helper(TreeNode* root)
    {
        if(root==nullptr)
        {
            return 0;
        }
        int left=helper(root->left);
        int right=helper(root->right);
        if(left==-1 or right==-1 or abs(left-right)>1)
        {
            return -1;
        }
        return max(left,right)+1;
        
    }

优化

 【例子7】Count Complete Tree Nodes

计算完全二叉树的节点数

思路1，递归，在求高度depth（root，int d, int& sum,int& maxd）的时候，就可以计算得到最后一层的节点数sum，当d = maxd,且为叶子节点时，sum++，当d>maxd时，sum = 1。当然，这样的做法TLE了。考虑优化，发现，在判断是否为叶子节点时，只需用root->right是否为空即可，还是TLE。这就需要换一种思路了。

思路2，求出最左边的高度和最右边的高度，看看是否相等，相等就说明二叉树是满的，节点数就是(1<<depth)-1，否则就求左右子树的节点数，再加上1。

思路3，root的左右子树，必定有一棵是满二叉树。如果root.right是一颗满二叉树，高度是h，那么，root.right、加上root 的节点数就刚好是2<<h， 这时候，就只再加上计算root.left即可。反之亦然。那么，如果判断一颗子树是否为满二叉树呢？可以判定root.right与root两个节点的左路边高度差，如果刚好是-1，就说明，right的最左节点和root的最左节点在同一层，root.left是满二叉树，再令root=root.left；反过来，如果高度差是-2，就说明right的最左边和最右边都是在同一层，right是满二叉树，再令root = root.left。

代码：

int countNodes(TreeNode* root) {
        if(!root) return 0;
        int sum = 0, maxd = 0;
        int d = depth(root,0,maxd,sum);
        int res = sum + (1<<(d-1)) - 1;
        // cout << maxd << " " << sum << " " << d;
        return res;
    }
    
    int depth(TreeNode *root, int d, int& maxd, int& sum){
        if(!root)return 0;
        if(!root->right){
            if(d>maxd){
                sum = 1;
                maxd = d;
            }else if(d==maxd){
                sum ++;
            }
        }
        int L = depth(root->left,d+1,maxd,sum), R = depth(root->right,d+1,maxd,sum);
        return max(L,R)+1;
    }

TLE

 int countNodes(TreeNode* root) {
        int cnt = 0,h = hight(root);
        while(h){
            int rh = hight(root->right);
            cnt += 1<<rh;
            if(h-rh==1) root = root->right;
            else root = root->left;
            h --;
        }
        return cnt;
    }
    
    int hight(TreeNode *root){
        int h = 0;
        while(root){
            root = root->left;
            h++;
        }
        return h;
    }

思路3

 【例子8】236. Lowest Common Ancestor of a Binary Tree

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself).”

        _______3______
       /                  ___5__          ___1__
   /      \\        /         6      _2       0       8
         /           7   4

思路：用分治法，先考虑root是lowest ancestor的情况，当p和q中有一个等于root，返回root，如果左右子树中都找到相应的节点，同样也返回root。如果这些都不行，就考虑对左右两个子树进行递归。我最开始想写一个寻找节点的函数，find(root,p,q)只要找到一个节点是p或q就返回该节点。这是多余的做法，在原函数递归的过程中，就可以得到左右子树中是否有p或q节点。理由是，对左右子树进行递归时，得到l节点和r节点，分别表示p、q节点在该子树上面的最近祖先。如果p、q节点分别在左右子树，这两个递归的函数求得的将是各自节点本身，即l = p|q， r = p|q。

代码：

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root)return NULL;
        if(root==q||root==p)return root;
        TreeNode *l = lowestCommonAncestor(root->left,p,q);
        TreeNode *r = lowestCommonAncestor(root->right,p,q);
        return l?(r?root:l):(r?r:NULL);
    }

View Code

 

第四部分：树的变形

【例子1】156. Binary Tree Upside Down

Given a binary tree where all the right nodes are either leaf nodes with a sibling (a left node that shares the same parent node) or empty, flip it upside down and turn it into a tree where the original right nodes turned into left leaf nodes. Return the new root.

For example:
Given a binary tree {1,2,3,4,5},

    1
   /   2   3
 / 4   5

 

return the root of the binary tree [4,5,2,#,#,3,1].

   4
  /  5   2
    /    3   1  

思路：可以直接对树上的节点做出修改，例如，root->left->left = root->right, root->left->right = root.这里可以用递归来解决，先将左子树变形。

代码参考 https://www.cnblogs.com/prmlab/p/7294356.html

 public TreeNode upsideDownBinaryTree(TreeNode root) {
        if (root == null || root.left == null){
            return root;
        }
        
        TreeNode newRoot = upsideDownBinaryTree(root.left);
        root.left.left = root.right; // node 2 left children
        root.left.right = root; //node 2 right children
        root.left = null;
        root.right = null;
        return newRoot;
        
    
        
    }

View Code

 

 

 

第五部分：遍历专讲

递归

vector<int> Traversal(TreeNode* root) {
        vector<int> res1, res2, res3;
        pre(root,res1);
        in(root,res2);
        post(root,res3);
        return res1;
    }
    
void pre(TreeNode* r,vector<int>& v){
        if(!r)return;
        v.push_back(r->val);
        pre(r->left,v);
        pre(r->right,v);
    }  

void in(TreeNode* r,vector<int>& v){
        if(!r)return; 
        in(r->left,v);
        v.push_back(r->val);
        in(r->right,v);
    }   

void post(TreeNode* r,vector<int>& v){
        if(!r)return; 
        post(r->left,v);
        post(r->right,v);
        v.push_back(r->val);
    }   

View Code

 

用栈

vector<int> preorderTraversal(TreeNode* root) {
       vector<int> res;
       if(!root)return res;
       stack<TreeNode*>  s;
       s.push(root);
       TreeNode *cur;
       while(!s.empty()){
           cur = s.top();
           res.push_back(cur->val);
           s.pop();
           if(cur->right)s.push(cur->right);
           if(cur->left)s.push(cur->left);
       }
       return res;
    }

先序

      vector<int> inorderTraversal(TreeNode* root) {
          vector<int> res;
          if(!root)return res;
          stack<TreeNode*>  s;
          TreeNode *cur=root;
           while(cur||!s.empty()){
               if(cur){
                   s.push(cur);
                   cur = cur->left;
               }else{
                   cur = s.top();
                   s.pop();
                   res.push_back(cur->val);
                   cur = cur->right;
               }

           }
           return res;
        }

中序

后序见“栈” 的专题

https://www.cnblogs.com/hello-new-world/p/7289615.html

Morris

中序遍历

 

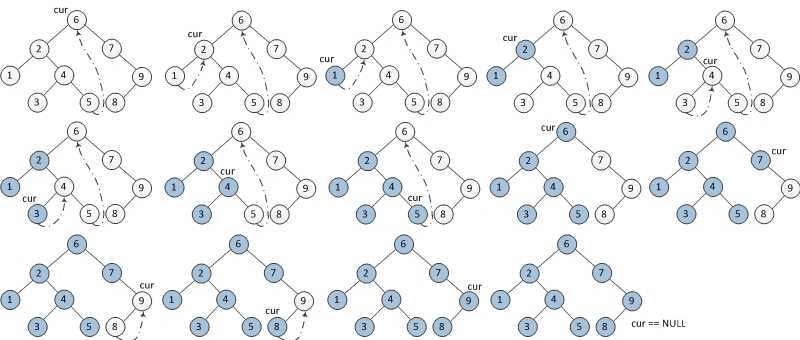
（图片来自https://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html）

思路：按照中序序列，建立每一个非叶子节点的前驱线索，即前驱节点的右指针指向当前节点，等输出前驱节点之后，直接访问该节点的右指针就到达了当前节点。

1、如果当前节点的左指针为空，则说明输出当前节点cur，cur变为当前节点的右节点。

2、如果当前节点的左指针不为空，则说明当前节点一定存在前驱pre，我们要找到这个pre节点，并且构建“线索”，即pre->right = cur。

　　a、找到前驱节点：如果cur->left是叶子节点，那么，pre就是cur->left了，否则，就需要寻找cur->left的最右叶子节点。

　　b、建立线索：找到pre节点了，如果这时候右指针为空，说明还没有建立线索，就令pre->right = cur。

　　c、完善左边线索：线索构建完毕，按照中序，我们还不能够输出当前的cur，而是应该令cur=cur->left,继续步骤1、2，这相当于完善左子树的线索。

　　这时可以发现，当cur从root到root的最左节点，这一路，除最左节点外，每个节点都建立了pre线索，所有前驱节点pre的right都指向当前节点cur。

　　d、按线索边遍历边拆桥：在输出最左节点之后，按照线索，cur变为它的右节点，由于左指针非空，继续寻找pre节点，发现，pre节点的右指针指向自己。这说明，线索已经建立了。这是第二次访问到当前节点了，于是，输出当前节点，别忘了“过河拆桥”，将线索消去，pre->right = NULL。同样的，这也说明左子树已经全部输出了，令cur = cur->right 即可。

代码：

View Code