2017多校第6场 HDU 6105 Gameia 博弈

Posted 2020-10-02 Lsxxxxxxxxxxxxx

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6105

题意：Alice和Bob玩一个游戏，喷漆！现在有一棵树上边的节点最开始都没有被染色。游戏规则是： 1，Alice和Bob只能选择未被染色的节点染色，Alice染色成白色，Bob为黑色 2. Alice最先开始 3. Bob有k次机会可以把树上的线段剪断 4. 最后树上有白色Alice胜利，否则是Bob胜利 5,Bob染色的时候，与他相邻的节点被强制染成黑色。

解法：​ 先考虑Alice胜利的情况：Alice如果胜利的话有两种可能

         1，最后落点是Alice

         2，游戏中间Alice就已经胜利了

         证明1：对于第一种来说，肯定是奇数个，但是是否能实现呢？答案是可以的，对于节点个数为奇数的树，Alice每次染色给叶子节点的父亲，那么Bob肯定只能染色这个叶子节点，Bob将会失去k次的优势，最后的落点是Alice，树上存在了白点，Alice胜利。

         证明2：考虑下面的图：

       

           当Alice放在f位置的时候其儿子成为了孤立节点，Alice只要放上一个就必赢，所以只要存在这样的结构Alice就胜利，也就是一个节点的“儿子数量” >= 2 ，这种结构并不是简单的数量上大于等于2，而是儿子的个数必须要是奇数个比如：

          

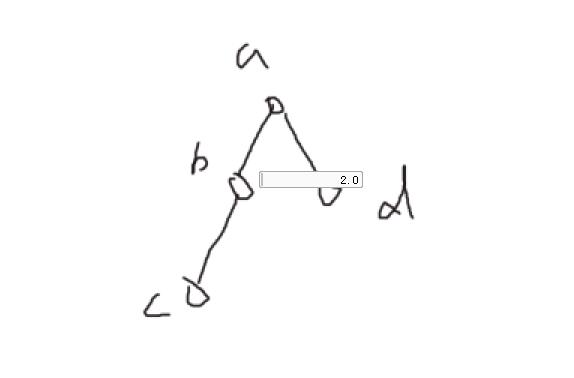
         就不行。但是下面这个可以

        

           那么剩下的情况就是Bob一定胜利吗？不是的，Bob如果想胜利的话n一定是偶数，并且必须可以利用他的k次机会把节点分成n/2部分，每一部分都是两个节点，否则还是会输，因为Alice先开始优势太大，比如：k = 0的时候

          

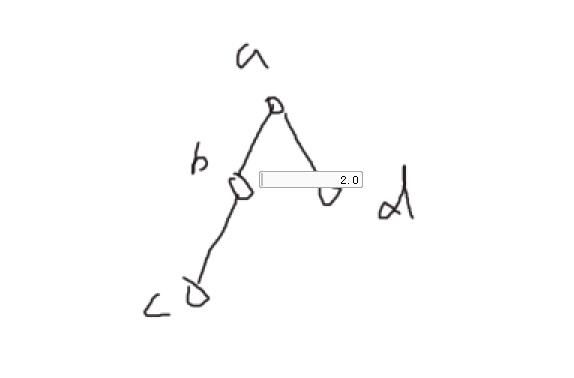
             Alice 染色c,Bob 染色b，那么a直接被染色，剩下Alice染色d胜利。

 

#include <bits/stdc++.h>
using namespace std;
const int maxn = 550;
int head[maxn], edgecnt;
struct node{
    int to,next;
}E[maxn*2];
void add(int u, int v){
    E[edgecnt].to=v,E[edgecnt].next=head[u],head[u]=edgecnt++;
}
void init(){
    memset(head,-1,sizeof(head));
    edgecnt=0;
}
int sz[maxn];
bool flag;
void dfs(int u, int pre){
    if(flag) return;
    sz[u] = 1;
    int ans = 0;
    for(int i=head[u]; ~i; i=E[i].next){
        int v = E[i].to;
        if(v == pre) continue;
        dfs(v, u);
        sz[u] += sz[v];
        if(sz[v]%2==1) ans++;
    }
    if(ans>=2) flag=1;
}

int main()
{
    int T,n,k;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d%d",&n,&k);
        flag=0;
        init();
        for(int i=2; i<=n; i++){
            int x;
            scanf("%d", &x);
            add(i, x);
            add(x, i);
        }
        dfs(1,-1);
        if(flag||n%2) printf("Alice\\n");
        else if(n/2-1>k) printf("Alice\\n");
        else printf("Bob\\n");
    }
    return 0;
}