最长公共子串+最长公共子序列

Posted 2020-10-02 xiaoxi666

两道题都可以用动态规划的方法做，只是状态转移方程不同。

 

最长公共子串（注意子串是连续的）

1、先建立一个二维数组array[str1.size()][str2.size()]（全部初始化为0），初始化第一行和第一列（元素相同处置1），然后进入状态方程

2、状态转移方程：

　　if(str1[i] == str2[i]) 　　array[i][j]=array[i-1][j-1]+1;　　（左上方对角线的值加上1）

　　否则无操作。

3、最后寻找整个array中的最大值即可（因为可能有多个子串）

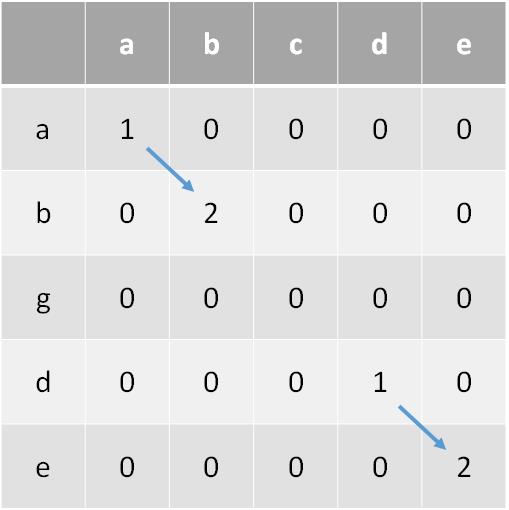
示意（图中有两个公共子串，分别为"ab"和"de"，长度都为2）

 

程序：

 1 /*
 2 本程序说明：
 3  
 4 最长公共子串（注意空格，不要用cin，要用getline）
 5  
 6 */
 7 #include <iostream>
 8 #include <vector>
 9 #include <string>
10 using namespace std;
11  
12 int largestCommentSubString(std::string str1,std::string str2){
13     if(0 == str1.length() || 0 == str2.length())
14         return 0;
15  
16     std::vector<std::vector<int> > array(str1.size(),std::vector<int>(str2.size(),0));
17     for(size_t i=0; i< str2.size(); ++i){
18         if(str1[0] == str2[i])
19             array[0][i]=1;
20     }
21     for(size_t i=0; i< str1.size(); ++i){
22         if(str2[0] == str1[i])
23             array[i][0]=1;
24     }
25     for(size_t i=1; i< str1.size(); ++i){
26         for(size_t j=1; j< str2.size(); ++j){
27             if(str1[i] == str2[j]){
28                 array[i][j]=array[i-1][j-1]+1;
29             }
30         }
31     }
32     int length=0;
33     for(size_t i=0; i< array.size(); ++i){
34         for(size_t j=0; j< array[0].size(); ++j){
35             if(array[i][j]>length){
36                 length=array[i][j];
37             }
38         }
39     }
40     return length;
41 }
42  
43 int main(){
44     std::string str1,str2;
45     while(getline(cin,str1),getline(cin,str2)){     
46         cout<<largestCommentSubString(str1,str2)<<endl;
47     }
48     return 0;
49 }

 

最长公共子序列（注意子序列可以不连续）

1、先建立一个二维数组array[str1.size()+1][str2.size()+1]（全部初始化为0），然后进入状态方程

2、状态转移方程：

　　if(str1[i] == str2[i]) 　　array[i][j]=array[i-1][j-1]+1;　（左上方对角线的值加上1）

　　if(str1[i] != str2[i]) 　　array[i][j]=max(array[i-1][j],array[i][j-1]);　　（左边和上边的最大值）

3、最后返回整个array中的最大值即可（即array右下角元素的值）

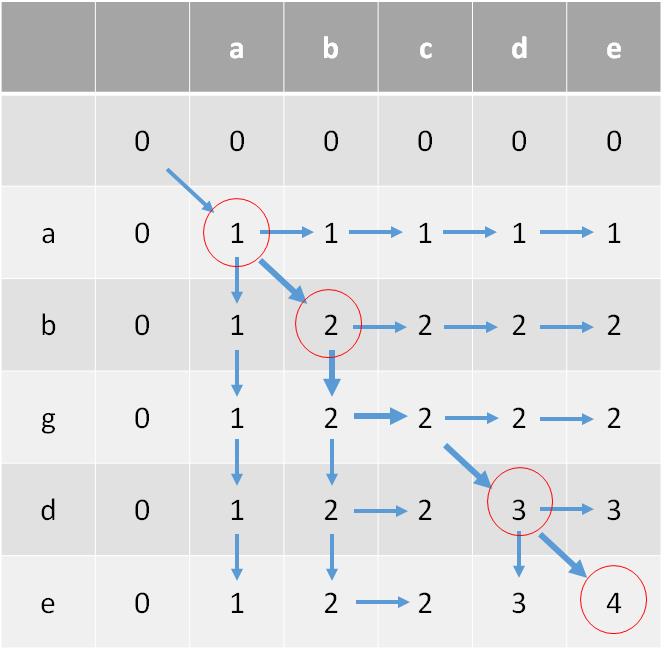
示意(图中的公共子序列为"abde"，注意我的程序是左面的和上面的相同的情况下，优先左，当然也可以是上)：

 

 1 /*
 2 本程序说明：
 3 
 4 最长公共子序列
 5 
 6 */
 7 #include <iostream>
 8 #include <vector>
 9 #include <string>
10 using namespace std;
11 
12 int findLCS(string str1,string str2) {
13     // write code here
14     if(0 == str1.size() || 0 == str2.size())
15         return 0;
16     vector<vector<int> > array(str1.size()+1,vector<int>(str2.size()+1,0));
17     for(size_t i=1; i<= str1.size(); ++i){//注意：是小于等于
18         for(size_t j=1; j<= str2.size(); ++j){//注意：是小于等于
19             if(str1[i-1] == str2[j-1]){//前面填充了一行一列，因此判断i-1和j-1
20                 array[i][j]=array[i-1][j-1]+1;
21                 }
22             else
23                 array[i][j]=max(array[i-1][j],array[i][j-1]);
24         }
25     }
26     return array[str1.size()][str2.size()];
27 }
28 
29 int main(){
30     string str1,str2;
31     while(getline(cin,str1),getline(cin,str2)){
32         cout<<findLCS(str1,str2)<<endl;
33     }
34     return 0;
35 }

 

如果还要进一步打印出其中一个公共子序列的话，需要用到回溯法。我们在动态规划时需要记录元素的状态，一步步回溯回去即可。

 1 /*
 2 本程序说明：
 3 
 4 最长公共子序列（加上了其中一个子序列的打印功能，回溯法）
 5 
 6 */
 7 #include <iostream>
 8 #include <vector>
 9 #include <string>
10 using namespace std;
11 
12 //打印（回溯法）
13 void printLCS(const string& str1,const string& str2,const vector<vector<string> >& flag,int i,int j,string& str)
14 {
15     if(0==i||0==j)
16         return;
17     if("left_up"==flag[i][j])
18     {
19         str.insert(str.begin(),str1[i-1]);//把要打印的公共字符逆序存在str中(因为回溯法从后向前，所以需要逆序)
20         printLCS(str1,str2,flag,i-1,j-1,str);
21     }
22     else if("left"==flag[i][j])
23         printLCS(str1,str2,flag,i-1,j,str);
24     else if("up"==flag[i][j])
25         printLCS(str1,str2,flag,i,j-1,str);
26 }
27 
28 int findLCS(const string& str1,const string& str2) {
29     // write code here
30     if(0 == str1.size() || 0 == str2.size())
31         return 0;
32     vector<vector<string> > flag(str1.size()+1,vector<string>(str2.size()+1,""));//记录状态
33     vector<vector<int> > array(str1.size()+1,vector<int>(str2.size()+1,0));
34     for(size_t i=1; i <= str1.size(); ++i){//注意：是小于等于
35         for(size_t j=1; j<= str2.size(); ++j){//注意：是小于等于
36             if(str1[i-1] == str2[j-1]){//前面填充了一行一列，因此判断i-1和j-1
37                 array[i][j] = array[i-1][j-1]+1;
38                 flag[i][j] = "left_up";
39             }
40             else
41             {
42                 if(array[i-1][j] >= array[i][j-1])
43                 {
44                     array[i][j] = array[i-1][j];
45                     flag[i][j] = "left";
46                 }
47                 else/*(array[i-1][j] < array[i][j-1])*/
48                 {
49                     array[i][j] = array[i][j-1];
50                     flag[i][j] = "up";
51                 }
52             }
53         }
54     }
55 
56     string str="";
57     printLCS(str1,str2,flag,str1.size(),str2.size(),str);
58     cout<<"公共子序列： "<<str<<endl;
59     return array[str1.size()][str2.size()];
60 }
61 
62 int main(){
63     std::string str1,str2;
64     while(getline(cin,str1),getline(cin,str2)){
65         cout<<findLCS(str1,str2)<<endl;
66     }
67     return 0;
68 }

 最长公共子序列扩展题（注意思维的转换）：

 1 /*
 2 本程序说明：
 3 
 4 给定一个数组，插入元素使得它成为回文串，要求所得回文串所有数字之和最小。
 5 
 6 */
 7 #include <iostream>
 8 #include <vector>
 9 #include <algorithm>
10 using namespace std;
11 
12 int main()
13 {
14     int n;
15     while(cin>>n){
16         vector<int> v(n);
17         int sum=0;
18         for(int i=0;i<n;++i){
19             cin>>v[i];
20             sum+=v[i];
21         }
22 
23         vector<int> rv=v;
24         reverse(rv.begin(),rv.end());
25 
26         //这段程序其实就是原数组和逆序数组求公共子序列，得到最大子序列的和，
27         //剩下要插入的数字之和就是原数组的和减去公共子序列的和
28         vector<vector<int>> dp(n+1,vector<int>(n+1,0));
29         for(int i=1;i<=n;++i){
30             for(int j=1;j<=n;++j){
31                 if(v[i-1]==rv[j-1]){
32                     dp[i][j]=dp[i-1][j-1]+v[i-1];
33                 }
34                 else{
35                     dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
36                 }
37             }
38         }
39 
40 //        for(int i=0;i<n+1;++i){
41 //            for(int j=0;j<n+1;++j){
42 //                cout<<dp[i][j]<<" ";
43 //            }
44 //            cout<<endl;
45 //        }
46 
47         cout<<sum+(sum-dp[n][n])<<endl;//其中sum-dp[n][n]是需要插入的数字和
48     }
49     return 0;
50 }

 

参考文章：http://www.cnblogs.com/huangxincheng/archive/2012/11/11/2764625.html