POJ3233 构造子矩阵+矩阵快速幂

Posted 2020-10-02 狡啮之仰

题意：给你矩阵A，求S=A+A^1+A^2+...+A^n

 

sol：直接把每一项解出来显然是不行的，也没必要。

我们可以YY一个矩阵：

其中1表示单位矩阵

 

然后容易得到：

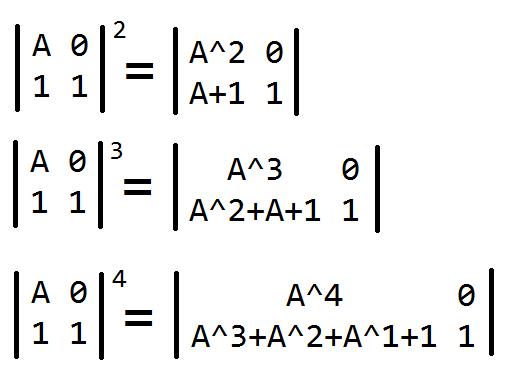
可以看出这个分块矩阵的左下角那块就可以得到要求的解S

我们取这一块，再减去一个单位矩阵1即可。

为了保持右下角一直是1，所以右上的位置必须是0，由于需要不断移位，所以1是必要的，A是必要的，所以第一列保证移位，

第二列保证保留1，因此我们能成功构造出....

这个题还可以根据等比矩阵的性质来进行求解...后面补(x

 

  1 #include <iostream>
  2 #include <stdio.h>
  3 #include <cstring>
  4 using namespace std;
  5 
  6 int n,k,mod;
  7 typedef long long ll;
  8 struct matrix{
  9     int row,col,ele[32][32];
 10     matrix(){};
 11     matrix(int row,int col):row(row),col(col){
 12         memset(ele,0,sizeof(ele));
 13     }
 14     void init(){
 15         row=col=n;memset(ele,0,sizeof(ele));
 16         for(int i=0;i<n;++i) ele[i][i]=1;
 17     }
 18     void clear(){
 19         row=col=n;
 20         memset(ele,0,sizeof(ele));
 21     }
 22     matrix operator *(const matrix& rhs){
 23         if(col!=rhs.row) printf("Exception...\\n");
 24         matrix c=matrix(row,rhs.col);
 25         for(int i=0;i<row;i++)
 26             for(int k=0;k<col;++k)
 27                 for(int j=0;j<rhs.col;++j)
 28                     c.ele[i][j]=(c.ele[i][j]+ele[i][k]*rhs.ele[k][j])%mod;
 29         return c;
 30     }
 31     matrix operator +(const matrix &rhs){
 32         if(row!=rhs.row||col!=rhs.col) printf("+ Exception\\n");
 33         matrix c=matrix(row,col);
 34         for(int i=0;i<row;++i)
 35             for(int j=0;j<col;++j)
 36                 c.ele[i][j]=(c.ele[i][j]+ele[i][j]+rhs.ele[i][j])%mod;
 37         return c;
 38     }
 39     void print(){
 40         for(int  i=0;i<row;++i){
 41             for(int j=0;j<col;++j)
 42                 printf("%d ",ele[i][j]);
 43             printf("\\n");
 44         }
 45     }
 46 };
 47 struct bigMatrix{
 48     int row,col;matrix ele[5][5];
 49     bigMatrix(){};
 50     bigMatrix(int row,int col):row(row),col(col){
 51         for(int i=0;i<row;++i)
 52             for(int j=0;j<col;++j) ele[i][j].clear();
 53     }
 54     void init(){
 55         row=col=2;
 56         for(int i=0;i<row;++i)
 57             for(int j=0;j<col;++j) ele[i][j].clear();
 58         for(int i=0;i<row;++i) ele[i][i].init();
 59     }
 60     bigMatrix operator *(const bigMatrix& rhs){
 61         if(col!=rhs.row) printf("Exception...\\n");
 62         bigMatrix c=bigMatrix(row,rhs.col);
 63         for(int i=0;i<row;i++)
 64             for(int k=0;k<col;++k)
 65                 for(int j=0;j<rhs.col;++j)
 66                     c.ele[i][j]=(c.ele[i][j]+ele[i][k]*rhs.ele[k][j]);
 67         return c;
 68     }
 69 };
 70 bigMatrix fastpow(bigMatrix a,ll b){
 71     bigMatrix ans;ans.init();
 72     // printf("%d %d %d %d\\n",a.row,a.col,ans.row,ans.col);
 73     if(b==0) return ans;
 74     while(b){
 75         if(b&1) ans=ans*a;
 76         a=a*a;
 77         b>>=1;
 78     }
 79     return ans;
 80 }
 81 int main(){
 82     while(~scanf("%d%d%d",&n,&k,&mod)){
 83         matrix A=matrix(n,n);
 84         for(int i=0;i<n;++i){
 85             for(int j=0;j<n;++j){
 86                 scanf("%d",&A.ele[i][j]);
 87                 A.ele[i][j]%=mod;
 88             }
 89         }
 90         bigMatrix mat=bigMatrix(2,2);
 91         matrix t=matrix(n,n);t.init();
 92         mat.ele[0][0]=A;mat.ele[0][1]=matrix(n,n);
 93         mat.ele[1][0]=t;mat.ele[1][1]=t;
 94         bigMatrix d=fastpow(mat,k+1);
 95         matrix B=d.ele[1][0];
 96         for(int i=0;i<n;++i) B.ele[i][i]=(B.ele[i][i]-1+mod)%mod;
 97         for(int i=0;i<n;++i){
 98             printf("%d",B.ele[i][0]);
 99             for(int j=1;j<n;++j){
100                 printf(" %d",B.ele[i][j]);
101             }
102             printf("\\n");
103         }
104     }
105     return 0;
106 }