2017.8.9数论课小结

Posted 2020-10-02 zbtrs

一、先是一些整除的性质：

•整除：若a=bk，其中a,b,k都是整数，则b整除a，记做b|a。

•也称b是a的约数（因数），a是b的倍数

•显而易见的性质：

•1整除任何数，任何数都整除0

•若a|b,a|c，则a|b+c, a|b-c

•若a|b，则对任意整数c，a|bc

•传递性：若a|b,b|c，则a|c

例1：

•例题：[CF 762A]k-th divisor

•求n的第k小的约数。如果不存在输出-1

•1 ≤ n ≤ 10^15, 1 ≤ k ≤ 10^9

分析：这道题显然不能用O(n)次枚举出答案，如果能做到O(sqrt(n))就好了，事实上确实如此，因为每一个数的因数都是成对出现的，所以我们枚举sqrt(n)以内的因数就能得到范围以外的所有因数，将所得答案排序即可.

二、然后是一些质数和合数的性质：

•若大于1的正整数p仅有两个因子1和p，则称p是一个质数（素数）。

•否则，若p>1，则称p是一个合数。

•1不是质数也不是合数

•若n是一个合数，则n至少有1个质因子。因此其中最小的质因子一定不大于sqrt(n)

•质数有无穷多个。不大于n的质数约有n/ln(n)个。

•唯一分解定理：把正整数n写成质数的乘积（即n=p1p2p3...pk，其中pi为质数且单调不减），这样的表示是唯一的。

例2：

•例题：[CF 776B]Sherlock and his girlfriend

•n个点，标号2..n+1，

•给这些点染色，要求若a是b的质因子，则a和b的颜色不同。

•求一种颜色数最少的方案

•n≤10^100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

 分析：这个数据范围是吓你的，因为看到这个数据范围根本就无从下手嘛，连O(logn)都跑不过，除非O(1),不过确实是O（1），仔细分析一下，我们只需要2种颜色即可，质数一种颜色，合数一种颜色就可以了，原因就是合数的质因数是质数，而质数没有因数。

关于怎么分解质因数：

void fenjie(int x)
{
    for (int i = 2; i <= sqrt(x); i++)
    {
        while (x % i == 0)
        {
            if (!vis[i])
            {
                vis[i] = 1;
                ans[++tot] = i;
            }
            x /= i;
        }
    }
    if (x > 1)
        ans[++tot] = x;
}

分析：这个算法的关键有三个：1.如果除以一个因数就把它除尽. 2.记录这个数有没有进入答案. 3.最后可能还剩下一个数，至于为什么能剩下一个数，我们有一个很重要的定理：每一个数的质因数只有一个大于sqrt(n)的，根据唯一分解定律可以很容易证明.
下面是同余和带余除法的相关知识：

•对于整数a,b，b>0，则存在唯一的整数q,r，满足a=bq+r，其中0≤r<b。

•其中称q为商、r为余数。

•余数用a mod b表示。

•若两数a,b除以c的余数相等，则称a,b模c同余，记做a≡b(mod c)。

•性质：a≡b(mod c)与c|a-b等价

•推论：若a≡b(mod c),d|c，则a≡b(mod d)

例3：奶牛分厮：传送门(应用了第五行的性质)

三、下面是一些最大公约数的知识：

•一些性质：

•(a,a)=(0,a)=a

•若a|b，则(a,b)=a

•(a,b)=(a,a+b)=(a,ka+b)

•(ka,kb)=k·(a,b)

•(a,b,c)=((a,b),c)

•若(a,b)=1，则称a,b互质（互素）

•互质的两个数往往有很好的性质

我们来证明一下第三条：

直接证明(a,b) = (a,a+b)很难，但是我们如果能证明a,b的因数和a,a+b的因数完全相同就好了，我们假设任意一个a,b的公因数p,p是a,b的因数，那么p也是a+b的因数，这样完成了从(a,b)向(a,a+b)的推导，至于如何反过来推导，将过程稍加修改一下即可，那么第二个等式也很容易出来了。这个证明利用的是整除的性质和我们的假设：任意的因数。

•例4：[CF 664A]Complicated GCD

•求gcd(a, a+1, a+2, ..., b)

•1≤a≤b≤10^100

分析：这个数据范围还是吓你的，可以很快的知道(a,a+1) = 1,任意两个相邻的正整数的gcd都为1，然后利用最后一条性质即可推出答案为1.至于为什么(a,a+1)=1呢？可以利用欧几里得算法：(a+1,a) = (a,1)= 1.

•例5：[CF 757B]Bash\'s Big Day

•给定n个正整数{ai}

•求一个子集S，满足gcd(S1, ..., Sk)>1，同时|S|尽可能大。

•1≤n,ai≤10^5

分析：一个一个去分解质因数肯定是不行的，但是我们可以利用像dp中的刷表法一样，从已知状态向未知状态扩展，假设我们枚举因数2，我们可以从2开始枚举有哪些数既是2的倍数又是集合中的数，这样我们枚举质数到amax即可，但是这个算法复杂度是O(n^2)的，会TLE,有没有什么优化方法呢？

     其实对于这种枚举的优化，我们无非是减少枚举层数或者避免枚举一定不会有解的答案，可以发现，我们只需要枚举当前质因数的倍数就好了，这样才能满足2个条件.这样的话算法复杂度是O(max(ai)*In(max(ai))).

四、欧几里德算法

•又称辗转相除法

•迭代求两数gcd的做法

•由(a,b)=(a,ka+b)的性质：gcd(a,b)=gcd(b, a mod b)

•容易证明这么做的复杂度是O(log n)

•int gcd(int a, int b) {
    if (b==0) return a;
    return gcd(b, a % b);
} 

五、•裴蜀定理：

•设(a,b)=d，则对任意整数x,y，有d|ax+by成立；

•特别地，一定存在x,y满足ax+by=d

•等价的表述：不定方程ax+by=c(a,b,c为整数)有解的充要条件为(a,b)|c

•推论：a,b互质等价于ax+by=1有解

这个定理是为什么不定方程有解的理论依据.

六、扩展欧几里德算法

 扩展欧几里得算法主要是用来解决形如ax+by=c这类方程的问题的，考虑怎么解这个方程，利用欧几里得算法，我们可以把原方程变为：

bx\'+(a - pb)y\' = c,变为a和b的主元方程：ay\' + b(x\' - py\'),其中p是a/b得到的商，那么我们就能得到x=y\',y = x\'-py\',这样一直计算下去，可以

借助欧几里得算法的结果得到x\'\'=1,y\'\' = 0,传递上来，就能得到x,y的值.我们可以考虑递归实现这个算法：

 

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a%b, x, y);
    int t = x;
    x = y;
    y = t - a / b*y;
    return r;
}

这只是一组特解，如果我们要求出所有解该怎么办？可以得到一个解系：x = x0 + kb,y = y0 - ka。

不过运用这一个算法有个重要的前提，我们要求解的ax+by=c的c必须等于gcd(a,b),如果不等于该如何处理呢，可以看我的另一篇博客：青蛙的约会：传送门

另外，第一件事要先判断有没有解，利用裴蜀定理即可.

七、逆元

•若ax≡1 (mod b)，则称x是a关于模b的逆元，常记做a^(-1)。

•回忆同余的性质。上式等价于ax+by=1

•如何求逆元？等价于解方程ax+by=1

•因此逆元不一定存在：
存在的充要条件为(a,b)=1

•推论：p是质数，p不整除a，则a模p的逆元存在。

 •结论：在[0,b)的范围内，a关于模b的逆元(若存在)是唯一的。

我来证明一下最后一个结论：如果存在两个逆元x1<x2<b,那么

ax1≡ax2≡1 (mod b) ,利用第一个同余式，a(x2-x1) % b == 0,

b不整除a,那么b整除x2-x1,而x2-x1 < b,所以矛盾，故结论成立.

int inv(int a, int b) {
    int x, y;
    exgcd(a, b, x, y);
    return x;
}

八、线性求逆元

如何O(n)求1~n模质数p的逆元？

我们肯定是要用O(1)复杂度来求出每一个数的逆元，那么一定要用到数学公式和之前推导出的值，我们怎么样才能使它强制出现以前计算过的逆元呢？

余数！我们知道余数小于除数，利用这个性质，我们可以得到：p≡0 (mod p) -----> iq+r≡0 (mod p),为了出现i的逆元，消掉r,我们同时乘i^(-1)r^(-1)即可，得到

qr^(-1)+i^(-1)≡0 (mod p),那么i的逆元就等于-qr^(-1).

for (inv[1] = 1, i = 2; i <= n; ++i)
    inv[i] = (p - p / i) * inv[p % i] % p;

程序里是p-p/i而不是p/i是为了避免负数.

•例6：组合数取模

•回答T次询问

•每次询问C(n, k) mod 998244353(一个质数)

•T≤10^5，0≤k≤n≤10^7

分析：大组合数是一个非常经典的求逆元的问题，我们知道%操作只有+,-,*三种操作，没有除法，但是可以利用逆元处理：a/b mod c = a * b^(-1) mod c,为什么是这样呢,我们把第一个式子乘b*b^(-1),因为1mod任何数还是1，所以等式成立，我们如果要求n^(-1)!,我们可以直接把1^(-1) * 2^(-1)*...*n^(-1),利用线性求逆元即可，因为有多个询问，保存下答案.

九、线性筛

•考虑一个经典问题：求不大于n的所有素数。

•Eratosthenes筛法：

•1.初始时令列表A={2,3,...,n};p=2

•2.枚举所有p的倍数(不包括p)，并在A中删去这些数

•3.令p为A中的下一个数并跳转至(2)。如果不存在下一个则结束。

•4.算法结束时，A中剩下的数为不大于n的所有素数。

这个算法没什么好说的，就是求出补集，然后用全集减去补集就是我们所求的.

int sieve(int n, bool isprime[], int prime[]) {
    int tot = 0;
    for (int i = 2; i <= n; ++i) isprime[i] = 1;
    for (int i = 2; i <= n; ++i)
        if (isprime[i]) {
            prime[++tot] = i;
            for (int j = i + i; j <= n; j += i)
                isprime[j] = 0;
        }
    return tot;
}

复杂度O(nloglogn)
例7：求[1,10^7]内的所有素数。内存限制1MB

分析：内存只有1mb开不下这么大的数组，但是只要求一个答案，我们可以分段来做，假设我们分为k段，第i段为[l,r],我们枚举不超过sqrt(r)的素数并筛掉[l,r]的数即可,只是枚举素数总要保存的吧，那么我们用一种比较玄学的方法：保存[1,sqrt(10^7)]的素数，这样如果区间被覆盖在左边，直接就可以得到答案，如果被覆盖在右边，我们也稍微枚举一下就好了.

但是这个复杂度还是太高，能不能做到O(n)呢？其实可以，如果我们能够保证每一个数只被删除一次就可以了，怎么保证呢？我们利用数的最小分解来分析：比如一个数18，它的分解是唯一的，但是分解的数的排列并不是唯一的，比如2*3*3,3*2*3,我们只让它被第一个删除，怎么样才能做到呢？我们每次添加一个比当前已经分解的最小的质数更小的质数，比如已有了3*3,我们就只能添加2,如果已有2*3,我们就不能再继续搜了，为什么呢？如果我们添加一个5，5*2*3可以先被2*3*5搜到,这样被重复搜索了.这个线性筛的本质就是我们强行给它定一个搜索的顺序和限制，使得每一个数只能被删除一次.

int sieve(int n, int f[], int prime[]) {
    int tot = 0;
    for (int i = 2; i <= n; ++i) {
        if (!f[i]) prime[++tot] = f[i] = i;
        for (int j = 1; j <= tot; ++j) {
            int t = i * prime[j];
            if (t > n) break;
            f[t] = prime[j];
            if (f[i] == prime[j]) break;
        }
    }
}

这个代码中f[i]就是i被分解的最小质因数，如果我们枚举的素数正好等于f[i],也就不能继续了.

十、线性同余方程

•形如ax≡c (mod b)的方程，称为线性同余方程。

•等价于ax+by=c；因此有解条件为(a,b)|c

其实如果要求出x,我们只需要解出这个方程即可，其实还有简便做法：

如果(a,b) = 1,我们两边同时乘a^(-1),可以得到x≡a^(-1)c (mod b)

如果(a,b) != 1,因为(a,b)|c,所以说我们可以将a,b,c同时除以(a,b),然后

参照上面那种做法即可.

不过解方程和这种做法差不多，基本上都要做扩展欧几里得算法，不过后

一种做法可以得到一个定理：

•任意的线性同余方程总可以判定为无解、或化为x≡a (mod m)的形式。

十一、中国剩余定理

•考虑形如x≡ai (mod mi)的若干方程联立得到的方程组，如：

•x≡2 (mod 3) ............ (1)

•x≡3 (mod 5) ............ (2)

•x≡5 (mod 7) ............ (3)

•下面是一种可行的解法：

•由(1)设x=3y+2,代入(2)得到3y+2≡3(mod 5),解得y≡2(mod 5)

•设y=5z+2,代入(3)得到3(5z+2)+2≡5(mod 7),解得z≡4(mod 7)

•设z=7k+4,则x=3(5(7k+4)+2)+2=105k+68

•因此x≡68(mod 105)

 这个就相当于不同的换元，最终化简得到答案，不过这样做实在是太麻烦，有没有更简单一点的方法呢？

我们可以用中国剩余定理！

这个定理非常的巧妙，对于同余方程组x≡ai(mod mi) (i=1...n)，若mi两两互质，则x在mod M下有唯一解。这里M=m1m2...mn,

我们先看一下怎么构造解：设Mi = M/mi,那么(M,Mi) = 1,有关于模mi的逆元存在，设Mi的逆元为ti,那么Mi*ti ≡ 1 (mod mi), 

对于任意一个mj,j!=i,因为Mi包含了因数mj,所以Mi*ti ≡ 0 (mod mj),这样我们排除了其它模数的干扰，这两个式子前面同时乘上ai,得到：

aiMiti≡ai (mod mi), aiMiti≡0 (mod mj) (j≠i)，把得到的第一个式子累加起来，就得到了解x≡a1M1t1+a2M2t2+...+anMntn (mod M).

 

int CRT(const int a[], const int m[], int n) {
    int M = 1, ret = 0;
    for (int i = 1; i <= n; ++i) M *= m[i];
    for (int i = 1; i <= n; ++i) {
        int Mi = M / m[i], ti = inv(Mi, m[i]);
        ret = (ret + a[i] * Mi * ti) % M;
    }
    return ret;
}

例8：今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?

分析：

用中国剩余定理构造解。

ai = {2, 3, 2}, mi = {3, 5, 7}, M = 3 * 5 * 7 = 105

Mi = {105 / 3, 105 / 5, 105 / 7} = {35, 21, 15}

mi = {inv(35, 3), inv(21, 5), inv(15, 7)} = {2, 1, 1}

x ≡ 2 * (35 * 2) + 3 * (21 * 1) + 2 * (15 * 1)

x ≡ 233 ≡ 23 (mod 105)

 例9：

•组合数取模2

•回答T次询问，

•每次询问C(n, k) mod 1029471131

•1029471131 = 13*317*249811

•T≤105, 0≤k≤n≤1018

 分析：我们平常mod一个数都是mod质数，可是这次是个合数我们该如何解决呢？其实可以发现这个就是个中国剩余

定理的模板题，我们求出这个数mod13,mod317,mod249811的值，可以发现这3个数都是互质的，然后我们利用中国

剩余定理就能解出来.

 

这个定理可以将k和n快速缩小的p以内的范围中，以便减少复杂度.缩小后直接用组合数公式计算，同时线性求一下逆元即可.

十二、欧拉函数

 

第二个证明的n=p1^k1*p2^k2*...*pn^kn,不等于第一个证明中的n,当初为此迷惑了半天......

由此可以看出积性函数可以先拆成乘积的形式然后再合并就能得到公式.

欧拉函数的性质：1.phi(p^k)=(p-1)*p^(k-1)  2.积性函数(当a,b互质时！)  3.当b是质数，a%b==0，phi(a*b)=phi(a)*b,显然也可以利用积性函数来得到.

代码：

int phi(int x) {
    int ret = x;
    for (int i = 2; i * i <= x; ++i)
        if (x % i == 0) {
            while (x % i == 0) x /= i;
            ret = ret / i * (i - 1);
        }
    if (x > 1) ret = ret / x * (x - 1);
    return ret;
}

这份代码先除后乘的原因是防止溢出，我们在比赛的时候，如果数据范围大也要这么处理！

其实欧拉函数也可以像筛素数那样打一个表出来，具体的实现：

for(i=1; i<=maxn; i++)
    p[i]=i;
for(i=2; i<=maxn; i+=2)
    p[i]/=2;
for(i=3; i<=maxn; i+=2)
    if(p[i]==i)
    {
        for(j=i; j<=maxn; j+=i)
            p[j]=p[j]/i*(i-1);
    }

 

 

 例10：

                                                                                                                                                                                    2705: [SDOI2012]Longge的问题

Time Limit: 3 Sec  Memory Limit: 128 MB
Submit: 3160  Solved: 1973
[Submit][Status][Discuss]

Description

Longge的数学成绩非常好，并且他非常乐于挑战高难度的数学问题。现在问题来了：给定一个整数N，你需要求出∑gcd(i, N)(1<=i <=N)。

Input

一个整数，为N。

Output

一个整数，为所求的答案。

Sample Input

6

Sample Output

15

HINT

 

【数据范围】

对于60%的数据，0<N<=2^16。

对于100%的数据，0<N<=2^32。

 

 

Source

round1 day1

分析：如果直接暴力求gcd,n^2的枚举时间加上每次求gcd的时间，直接爆掉，那么能不能用更好的方法做呢？

       我们可以换个思路，要求Σgcd(i,n),我们假设gcd(i,n) = g,也就是我们要求以g为最大公约数的(i,n)有多少对，然后g对答案的贡献就是g*个数，显然，这个g是n的约数，对于约数的枚举我们有一个技巧，就是只枚举到它的sqrt即可，和它成对的一个约数就是n/i，前提是i != sqrt(n).如果g = 1,我们可以直接用欧拉函数来统计，如果g != 1呢？那么我们可以把i,n写作i = i\'*g,n = n\'*g,i和n同时除以g,那么n和i就互质了，这样直接用欧拉函数就可以解决问题了.

 

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

long long n,ans;

long long phi(long long x)
{
    long long res = x;
    for (long long i = 2; i <= sqrt(x); i++)
    {
        if (x % i == 0)
        {
            while (x % i == 0)
                x /= i;
            res = res / i * (i - 1);
        }
    }
    if (x > 1)
        res = res / x * (x - 1);
    return res;
}

int main()
{
    scanf("%lld", &n);
    for (long long i = 1; i <= sqrt(n); i++)
    {
        if (n % i == 0)
        {
            ans += i * phi(n / i);
            if (i * i < n)
                ans += n / i * phi(i);
        }
    }
    printf("%lld\\n", ans);

    return 0;
}

 例11：

2186: [Sdoi2008]沙拉公主的困惑

Time Limit: 10 Sec  Memory Limit: 259 MB
Submit: 4549  Solved: 1567
[Submit][Status][Discuss]

Description

　　大富翁国因为通货膨胀，以及假钞泛滥，政府决定推出一项新的政策：现有钞票编号范围为1到N的阶乘，但是，政府只发行编号与M!互质的钞票。房地产第一大户沙拉公主决定预测一下大富翁国现在所有真钞票的数量。现在，请你帮助沙拉公主解决这个问题，由于可能张数非常大，你只需计算出对R取模后的答案即可。R是一个质数。

Input

第一行为两个整数T，R。R<=10^9+10，T<=10000，表示该组中测试数据数目，R为模后面T行，每行一对整数N，M，见题目描述 m<=n

Output

共T行，对于每一对N，M，输出1至N！中与M！素质的数的数量对R取模后的值

Sample Input

1 11
4 2

Sample Output

1

数据范围：
对于100%的数据，1 < = N , M < = 10000000

分析：这道题又卡时间又卡空间......

       首先这道题要求互质的个数肯定要用欧拉函数来做，但是欧拉函数只能处理[1,m!]内的数，那么(m!,n!]内的数我们该怎么处理呢？要做出这道题，我们需要知道一个性质，如果x与m!互质，那么x+m!与m!互质，x+n*m!也与m!互质,所以我们处理一下[1,m!]内与m!互质的数的个数，然后利用这个性质就可以求出答案为φ(m!) * (n!) / (m!),这个φ(m!)可以化简一下：m!*π((pi-1) / (pi)),带入式子，得到答案为(n!) * π((pi - 1)/pi).

       因为有多个询问，所以我们先预处理出最大范围内的质数和逆元还有！，处理的方法是线性筛和线性求逆元，这里有一个优化就是能开bool尽量开bool，我之前开成long long就T了.

       现在还有一个问题就是爆空间，我们可以先打一个程序处理出1~10000000内的质数，可以发现质数的个数大约是664580个，数组刚好开这么大就可以过了.

 

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn = 10000001;

int t, p,n,m;
long long f[maxn], ans[maxn],prime[664580],niyuan[maxn];
bool vis[maxn];

void init()
{
    long long tot = 0;
    for (int i = 2; i <= maxn; i++)
    {
        if (!vis[i])
            prime[++tot] = i;
        for (int j = 1; j <= tot; j++)
        {
            if (prime[j] * i > maxn)
                break;
            vis[prime[j] * i] = 1;
            if (i % prime[j] == 0)
                break;
        }
    }
    f[1] = 1;
    for (int i = 2; i <= maxn; i++)
        f[i] = f[i - 1] * i % p;
    niyuan[1] = 1;
    for (int i = 2; i <= maxn && i < p; i++)
        niyuan[i] = (p - p / i) * niyuan[p % i] % p;
    ans[1] = 1;
    for (int i = 2; i <= maxn; i++)
    {
        if (!vis[i])
            ans[i] = ans[i - 1] * (i - 1) % p * niyuan[i % p] % p;
        else
            ans[i] = ans[i - 1];
    }
}

int main()
{
    scanf("%d%d", &t, &p);
    init();
    for (int i = 1; i <= t; i++)
    {
        scanf("%d%d", &n, &m);
        printf("%d\\n", f[n] * ans[m] % p);
    }

    return 0;
}

 十三、欧拉定理

不过求逆元一般是用扩展欧几里得来做，常数小，效率高,这两种方法的限制较多.

 

欧拉定理一个非常厉害的应用就是可以降低次数，一般的特征是a^b mod p,b非常大（甚至是正无穷），φ(p)比较小.

例12：

3884: 上帝与集合的正确用法

Time Limit: 5 Sec  Memory Limit: 128 MB
Submit: 2462  Solved: 1093
[Submit][Status][Discuss]

Description

 

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

 

一句话题意：

 

 

Input

 

接下来T行，每行一个正整数p，代表你需要取模的值

 

Output

T行，每行一个正整数，为答案对p取模后的值

 

Sample Input

3
2
3
6

Sample Output

0
1
4

HINT

 

对于100%的数据，T<=1000,p<=10^7

分析：这道题是欧拉定理的经典应用，一开始看到题面的我想到的就是找规律，可是涉及到∞，脑洞太小想不出来，但是它给定的模数是有限的，我们能不能从这个模数下手呢？

 

       我们接下来有两种思路：1.把模数越变越小，到最后直接出结果，类似于递归的过程 2.把次数的无穷化为有限，一般而言可以用欧拉定理和费马小定理，但是这道题给的模数不一定满足费马小定理的条件，欧拉定理也不一定满足，但是我们可以用欧拉定理的推论来解决.这两个思路结合起来就是本题的解.

       那么我们设答案为f(p), --图片摘自Codeplay0314的博客.

       注意边界，φ（x）= 0,当x = 1的时，因为如果x=1,显然原题是无解的.

这道题也说明了：若存在，那么也一定存在。当m=1时，存在，所以

 

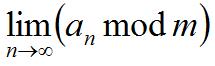对于所有正整数m,都有存在.

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int t, p;

long long qpow(long long a, long long b, long long mod)
{
    long long res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

long long phi(int x)
{
    long long res = x;
    for (long long i = 2; i <= sqrt(x);i++)
    {
        if (x % i == 0)
        {
            while (x % i == 0)
                x /= i;
            res = res / i * (i - 1);
        }
    }
    if (x > 1)
        res = res / x * (x - 1);
    return res;
}

long long solve(int x)
{
    if (x == 1)
        return 0;
    long long t = phi(x);
    return qpow(2, solve(t) + t, x);
}

int main()
{
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &p);
        printf("%lld\\n",solve(p));
    }
return 0;
}

十四、积性函数

 

线性筛与积性函数之间有一定的联系，如果题目要求我们求出质数的同时求出欧拉函数值，我们可以利用积性函数的性质在筛法中求出欧拉函数值：

 

void shai()
{
    phi[1] = 1;
    for (int i = 2; i <= maxn; i++)
    {
        if (!vis[i])
        {
            prime[++tot] = i;
            phi[i] = i - 1;
        }
        for (int j = 1; j <= tot; j++)
        {
            int t = prime[j] * i;
            if (t > maxn)
                break;
            vis[t] = 1;
            if (i % prime[j] == 0)
            {
                phi[t] = phi[i] * j;
                break;
            }
            else
            phi[t] = phi[i] * phi[j];
        }
    }
}

现在来解释一下代码：这个线性筛和之前的模板不太一样，原理是相同的，当i % prime[j] == 0的时候就代表找到了最小表示的最小质数，不能继续往下筛了，如果i是一个质数，那么它的phi肯定是i-1，如果i,prime[j]互质，那么利用积性函数

以上是关于2017.8.9数论课小结的主要内容，如果未能解决你的问题，请参考以下文章

1.29数论课笔记

数论-素数筛法小结

PAT 数列的片段和简单数论

3.16课·········小结

软件工程课小结

节小结和习题课